１年で見える世界が変わる！大人のための高校数学講座
公開日
2023年6月17日
更新日
2025年4月6日
ビジネス・キャリアアップ・教養のための高校数学
大人になったからこそ分かる数学の深い魅力
「数学」と耳にすると、学生時代の苦い思い出がよみがえる方もいるかもしれません。しかし同時に数学を理解したいという憧れに近い感情を抱く方も多いのではないでしょうか？学生時代に学んだ数学はテストの点数や学力評価の象徴であったわけですが、実は数学とは人類が長年にわたり築き上げてきた生活を豊かに照らすための貴重な知識の集積なのです。学生時代は苦手だった数学も大人になって学んでみると、学生時代とは異なった発見や驚きを感じたり、何より数学という学問の「面白さ」を感じることができるでしょう。
日常に潜む数学
日常生活で数学を使う場面はあまりないと思われるかもしれません。しかし、実は現代社会は数学無しでは成り立たないほど様々な場面で数学が使われています。例えば皆さんが今ご覧になっているPCやスマホの画面。これは電気がないと動きませんが、その電気を制御するのは数学です。皆さんが今聞いている音はどうでしょうか？実は音も電気と同じく「波」で表現できることが知られており、これらの応用して電話が開発されたり、最近では不必要な音を消すことができるノイズキャンセリングという機能が搭載されたイヤホンなんてものもあります。こういった日常生活を便利にしてきた科学技術の根底には数学が潜んでいます。
そのような目で日常生活を眺めてみると身近にはたくさんの不思議があふれています。リンゴはなぜ木から落ちるのでしょう？テレビの受信機で使うパラボラアンテナはなぜあの形なのでしょうか？こういった疑問に数学は答えを出してくれます。「世界の仕組みを１つ説明できるようになる」、これだけでも数学を価値は十分にあると言えるでしょう。
苦手克服、あの頃追いつけなかった「数学」のスキルがあなたのものに！
このように数学は非常に価値があると言えるでしょう。しかしながら、日本では数学が苦手な方が非常に多いのも事実で、多くの方がお悩みを抱えているようです。そこでそのお悩みを解決するべく、数学をわかりやすく、楽しく、身に着ける「高校数学講座」を新たに新設しました。
こちらの講座は楽しむために数学を理解することを目的としています。ただ問題を解けるようになることがゴールではなく、その数学の歴史的な背景や日常での応用例など、受験を離れた大人だからこそ楽しめる視点で数学を学んでいきます。
また、多くの方からお子様に算数や高校数学を教えられるようになりたいとのご要望もいただいたため、カリキュラムスライドはお子様も見てわかるよう心掛け、復習動画も1年見放題となっております！！自己学習はもとより、お子様に高校数学を教えられるようになりたいといった方も大歓迎です！！
本カリキュラム4つの特徴
1. 視覚から理解する
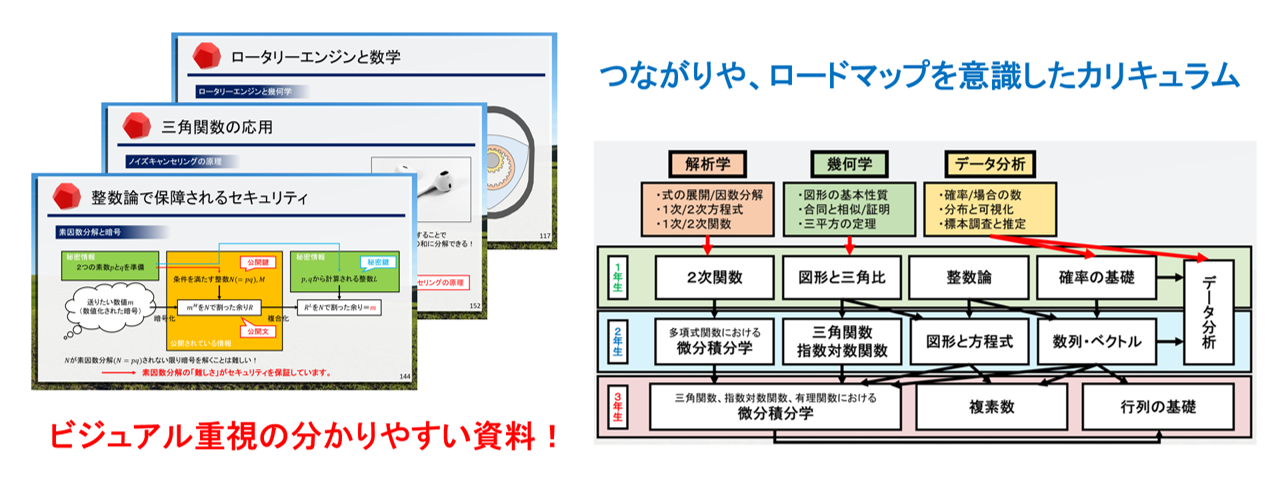
数式や計算ばかりではなく、視覚効果を利用した図や画像を多用することで、耳で聞くだけでなく、目から直接理解ができるスライド構成になっております。数字に苦手意識がある方でも「そうだったんだ！」と思えるような順序・構成になっています。
2. 歴史や必要性をしっかり学ぶ
「なぜこのような記号を使ったのか？」「この仕組みはどうやって生まれたのか？」といった謎は学問を学ぶ上では必ず現れます。本講座では、こうした時代背景や歴史、現在はどのように進歩しているのかなどもしっかりと学び、必要性や学ぶモチベーションに重きを置いた内容となっています。
3. 最も効率の良い順序・リズムで学ぶ
本カリキュラムでは授業順序を整理し、学ぶ上で最も効率のルートで授業を進めていきます。そのため、分野を無駄に行ったり来たりすることがなく、自然な流れで次の講義に進むことができます。さらに各ステップの終わりに「復習と展望（今後の流れ）」の時間を設けています。そのステップの内容をおさらいし、ご自身の理解度を確認していただくことができます。
4.丁寧な資料と復習動画提供
講義で配布する資料はこれだけを読んでも内容が理解できるように、丁寧に作り込んでいます。また、講義の動画は録画し1年間公開いたしますので、いつでも復習ができるシステムとなっております。
※今後の開催日程については、順次公開いたします。詳細はお問い合わせください。
受講対象
・高校数学を学び直したい方
・数学の苦手意識を克服したい方
・数学や計算、幾何学の歴史に興味がある方
・数学的思考力を身に着けたい方
・家族で数学の学習を進めてみたい方
・高卒認定や統計検定、数学検定などの資格試験に向けて理解を深めたい方
・大学や大学院の授業の中で高校数学までの理解が必要になりお困りの方
必要な数学知識
セミナー内容
クリックすると各範囲の詳細が表示されます。
１st grade -数学IA範囲-
第1回 数の展開と因数分解①
- ・式の展開
- ・因数分解
- ・実数と有理数
- ・平方根と有理化
第2回 1次方程式と不等式①
- ・1次方程式
- ・1次不等式
- ・連立不等式
- ・1次不等式の応用
第3回 2次関数の基礎①
- ・基本的な2次関数
- ・平方完成
- ・2次関数のグラフ
- ・関数の平行移動
第4回 2次関数の基礎②
- ・2次関数の最大最小
- ・定義域と値域
- ・2次関数の応用
- ・比例/反比例の活用
第5回 2次方程式と不等式
- ・2次関数と直線の交点
- ・2次関数と2次方程式
- ・解の個数と交点の個数
- ・2次不等式と2次関数のグラフ
第6回 三角比の基礎
- ・直角三角形と性質
- ・三角比の定義
- ・角度と三角形
- ・三角比の基本的な性質
第7回 正弦定理と余弦定理
- ・三角比の拡張
- ・正弦定理
- ・余弦定理
- ・図形と計量
第8回 集合と命題
- ・集合と記号
- ・和集合と積集合
- ・論理と命題
- ・命題と包含関係
第9回 対偶法と背理法
- ・命題と条件
- ・逆・裏・対偶
- ・対偶法
- ・背理法
第10回 場合の数
- ・集合の要素数
- ・場合の数の基礎
- ・順列・組み合わせ
- ・二項係数と二項定理
第11回 確率の基礎①
- ・確率の定義
- ・確率の計算
- ・独立と排反
- ・余事象の確率
第12回 確率の基礎②
- ・反復試行の確率
- ・確率と期待値
- ・条件付き確率
- ・ベイズの定理
第13回 整数の性質
- ・素数について
- ・ユークリッドの互除法
- ・不定方程式
- ・合同式
第14回 整数の応用・活用
- ・オイラー関数
- ・フェルマーの小定理
- ・整数と暗号理論
- ・整数の理論と応用
第15回 図形の性質①
- ・三角形の五心
- ・三角形の比の公式
- ・円周角の定理
- ・円の内接と接線
第16回 図形の性質②
- ・方べきの定理
- ・基本的な作図問題
- ・立体図形の性質
- ・オイラーの多面体定理
第17回 データの集計と要約統計量
- ・データの集計
- ・データの要約
- ・平均値と中央値
- ・標準偏差
第18回 データの相関
- ・分散と共分散
- ・相関係数
- ・データの相関と散布図
- ・疑似相関
2 nd grade -数学ⅡB範囲-
第19回 数学ⅠAの振り返りと数学ⅡBの概要
- ・数学ⅠAの総復習
- ・数学ⅡBの流れと概説
第20回 整式と根
- ・整式の割り算と剰余の定理
- ・因数定理と根
- ・有理式
- ・等式と不等式の証明
第21回 高次方程式と複素数
- ・複素数の基礎
- ・2次方程式と複素数
- ・高次方程式
- ・代数学の基本定理
第22回 図形と方程式
- ・座標平面上の点と直線
- ・垂直条件と平行条件
- ・円の方程式
- ・円と直線
第23回 軌跡と領域
- ・軌跡と方程式
- ・アポロニウスの円
- ・不等式と領域
- ・線形計画法
第24回 三角関数とそのグラフ
- ・三角関数の基礎
- ・三角関数の性質と相互関係
- ・三角関数のグラフ
- ・三角関数の方程式①
第25回 加法定理と波の合成
- ・三角関数の加法定理
- ・三角関数の方程式②
- ・2倍角と半角の公式
- ・三角関数の合成
第26回 指数関数と指数法則
- ・指数の拡張と累乗根
- ・指数法則
- ・指数関数のグラフ
- ・指数関数と方程式
第27回 指数・対数関数とそのグラフ
- ・対数関数
- ・底の変換公式
- ・対数関数のグラフ
- ・常用対数とその応用
第28回 数列の基礎
- ・数列とは
- ・等差数列と等比数列
- ・数列の和
- ・階差数列
第29回 数列の漸化式と数学的帰納法
- ・数列の漸化式（等差数列と等比数列）
- ・数列の漸化式（その他の代表的な数列）
- ・数学的帰納法
- ・3項間漸化式
第30回 多項式関数の微分
- ・微分係数
- ・極限の計算
- ・導関数
- ・微分の基本公式
第31回 微分とグラフの概形
- ・微分と接線
- ・関数の増減と極大・極小
- ・関数のグラフの概形
- ・関数の最大・最小
第32回 不定積分と定積分
- ・不定積分の計算
- ・定積分の計算
- ・定積分と面積
- ・微積分の基本定理
第33回 ベクトルの基礎
- ・ベクトルの概念
- ・ベクトルの足し算/引き算
- ・ベクトルの成分表示
- ・ベクトルの内積
第34回 ベクトルの応用
- ・ベクトルの直交条件
- ・位置ベクトル
- ・ベクトル方程式
- ・空間ベクトル
第35回 確率変数と平均・分散
- ・確率変数
- ・確率変数の平均
- ・確率変数の分散
- ・確率変数の和と積
第36回 確率分布と確率密度関数
- ・確率変数と確率分布
- ・二項分布
- ・正規分布
- ・二項分布の正規近似
第37回 標本平均の分布と母数の推定
- ・標本調査と全数調査
- ・標本平均の平均と分散
- ・母平均の区間推定
- ・母比率の区間推定
第38回 数学ⅡBの振り返りと数学ⅢCの概要
- ・数学ⅡBの総復習
- ・数学ⅢCの概説
３rd grade -数学ⅢC（数学活用）範囲-
第39回 媒介変数表示と2次曲線
- ・2次曲線と方程式
- ・媒介変数表示
- ・リサージュ曲線
- ・サイクロイド曲線
第40回 複素数平面とド・モアブルの公式
- ・複素数平面
- ・極方程式
- ・ド・モアブルの定理
- ・高次方程式の解
第41回 数列の極限と関数の連続性
- ・数列の極限値
- ・無限級数の収束と発散
- ・関数の極限と連続性
- ・関数の微分可能性
第42回 微分とその応用①
- ・指数関数と自然対数
- ・指数関数・対数関数の微分
- ・三角関数の微分
- ・合成関数の微分
第43回 微分とその応用②
- ・初等関数の微分
- ・初等関数のグラフの概形
- ・接線と交点の問題
- ・最大最小問題
第44回 積分とその応用
- ・初等関数の不定積分
- ・初等関数の定積分
- ・部分積分
- ・置換積分
第45回 面積・体積・区分求積法
- ・面積の基本公式
- ・区分求積法
- ・回転体の体積
- ・弧の長さ
第46回 行列の基礎
- ・行列とは
- ・行列の演算
- ・対角行列、回転行列
- ・1次変換
第47回 行列とその応用・活用
- ・行列の連立方程式
- ・行列を用いた応用問題
- ・グラフ理論と行列
- ・回帰分析と行列
第48回 高校数学の総まとめ、その先の分野について
- ・微分積分学のその後
- ・行列の理論と線形代数
- ・金融経済と確率統計の数学
- ・高校数学から現代数学へ
セミナー基本構成
（1日で2回分の講義を行いますので、総受講日数は24日となります。）
※開催回ごとに多少構成が変わることがあります。
お持ち物と注意事項
お申し込み人数が最少催行人数に満たない場合、セミナーの開催を【中止】とさせていただくことがございますので予めご了承願います。
【中止】の場合には第1回開催日の7日前までにご登録のメールアドレスにメールにてご連絡いたします。
【中止】となった場合、お支払い済みの料金は全額ご返金いたします。
料金
◎分割支払い：税込16,500円/月 (総額198,000円)
※分割支払いはクレジットのみ対応可能
※一括支払いはクレジットもしくは銀行振込で対応可能
・会社名義や旧姓など、振り込み名が本人名義でない場合は事前にご一報下さい
◎開催2日前までに振込確認が取れない場合、会場URLをお送りできませんので特にご注意下さい
定員
特定商取引法に基づく表示
セミナー監修
岡本 健太郎（おかもと けんたろう）
＜講師略歴＞
学歴：九州大学大学院数理学府博士後期課程修了(数理学博士)
出身：山口県下関市
所属学会：日本数学会, 日本アクチュアリー会
資格：高等学校数学科教員免許（専修免許）, 統計検定1級（数理統計）
数理学の博士号を取得した切り絵アーティスト。
国立研究開発法人科学技術振興機構 研究開発戦略センター 特任フェロー（2021~2022）
ドイツのチュービンゲン大学に研究員として滞在経験あり。元日本学術振興会特別研究員。
数学教育にも力を入れており、学生から社会人まで、わかり易く授業を展開。指導可能範囲は中学・高校数学から、大学の教養・専門分野、データ分析まで幅広く対応。また「数学」を使ったアート活動（切り絵）を通して、数学の有用性だけでなく美しさや魅力について積極的に発信。
担当講師
※日程により一部講師が変わる事があります。
会場とスケジュール
第2クール ※開催中（途中参加可）
オンライン教室01日目 第01,02回 2024年11月10日(日) 13:00～15:00
02日目 第03,04回 2024年11月24日(日) 13:00～15:00
03日目 第05,06回 2024年12月08日(日) 13:00～15:00
04日目 第07,08回 2024年12月22日(日) 13:00～15:00
05日目 第09,10回 2025年01月05日(日) 13:00～15:00
06日目 第11,12回 2025年01月19日(日) 13:00～15:00
07日目 第13,14回 2025年02月02日(日) 13:00～15:00
08日目 第15,16回 2025年02月16日(日) 13:00～15:00
09日目 第17,18回 2025年03月02日(日) 13:00～15:00
10日目 第19,20回 2025年03月16日(日) 13:00～15:00
11日目 第21,22回 2025年03月30日(日) 13:00～15:00
12日目 第23,24回 2025年04月13日(日) 13:00～15:00
13日目 第25,26回 2025年04月27日(日) 13:00～15:00
14日目 第27,28回 2025年05月11日(日) 13:00～15:00
15日目 第29,30回 2025年05月25日(日) 13:00～15:00
16日目 第31,32回 2025年06月08日(日) 13:00～15:00
17日目 第33,34回 2025年06月22日(日) 13:00～15:00
18日目 第35,36回 2025年07月06日(日) 13:00～15:00
19日目 第37,38回 2025年07月20日(日) 13:00～15:00
20日目 第39,40回 2025年08月03日(日) 13:00～15:00
21日目 第41,42回 2025年08月24日(日) 13:00～15:00
22日目 第43,44回 2025年09月14日(日) 13:00～15:00
23日目 第45,46回 2025年09月28日(日) 13:00～15:00
24日目 第47,48回 2025年10月12日(日) 13:00～15:00
第3クール ※開催中（途中参加可）
オンライン教室01日目 第01,02回 2025年04月06日(日) 10:00～12:00
02日目 第03,04回 2025年04月20日(日) 10:00～12:00
03日目 第05,06回 2025年05月11日(日) 10:00～12:00
04日目 第07,08回 2025年05月25日(日) 10:00～12:00
05日目 第09,10回 2025年06月08日(日) 10:00～12:00
06日目 第11,12回 2025年06月22日(日) 10:00～12:00
07日目 第13,14回 2025年07月06日(日) 10:00～12:00
08日目 第15,16回 2025年07月20日(日) 10:00～12:00
09日目 第17,18回 2025年08月03日(日) 10:00～12:00
10日目 第19,20回 2025年08月17日(日) 10:00～12:00
11日目 第21,22回 2025年08月31日(日) 10:00～12:00
12日目 第23,24回 2025年09月14日(日) 10:00～12:00
13日目 第25,26回 2025年09月28日(日) 10:00～12:00
14日目 第27,28回 2025年10月12日(日) 10:00～12:00
15日目 第29,30回 2025年10月26日(日) 10:00～12:00
16日目 第31,32回 2025年11月09日(日) 10:00～12:00
17日目 第33,34回 2025年11月16日(日) 10:00～12:00
18日目 第35,36回 2025年12月07日(日) 10:00～12:00
19日目 第37,38回 2025年12月21日(日) 10:00～12:00
20日目 第39,40回 2026年01月11日(日) 10:00～12:00
21日目 第41,42回 2026年01月25日(日) 10:00～12:00
22日目 第43,44回 2026年02月08日(日) 10:00～12:00
23日目 第45,46回 2026年02月22日(日) 10:00～12:00
24日目 第47,48回 2026年03月08日(日) 10:00～12:00
