「数理統計」とは？

数理統計とは、統計学を数学的に体系化し、データの分析や推測を理論的に行う学問です。確率の理論をベースにして、「推定」や「仮説検定」などの手法を用いてデータから法則性を導きます。AIやデータ分析にも応用される重要な分野です。

データ分析の背後にあるものの理解

データ活用の重要性が高まる中、「エクセルでグラフは作れるけど、その裏にある理屈までは分からない…」と感じることはありませんか？
本講座では、そうした曖昧な感覚から一歩抜け出し、数式と理論に基づく“本当の統計的思考”を身につけることを目標にします。
公式の暗記だけではなく、「なぜそうなるのか」を腹落ちできるように丁寧に解説し、自信を持ってデータを扱える力を磨きます。

セミナー概要

本講座では、中学・高校レベルの数学を基盤とし、統計学の土台から応用までを6回にわたって体系的に学びます。集合や命題、場合の数からスタートし、確率の基本計算、分布モデル（正規分布・二項分布）を経て、区間推定や回帰分析など、ビジネスやデータ分析の現場ですぐに役立つ知識へと段階的にレベルアップします。また、単なる公式の暗記ではなく、「なぜそうなるのか」「どう使うのか」に重点を置き、数式が持つ意味をしっかりと腹落ちできる内容です。
（※本講座のより入門的な内容をこちらのセミナーでご案内しています。「社会人のための１から始める数理統計【入門編】」）

一部例をご紹介しましょう。

①区間推定とサンプルサイズの算出

数理統計の試験では、次のような問題が頻繁に出題されます。

ある工場で製造された製品の寿命（単位：時間）を調査するため、ランダムに 選んだ40 個の製品について平均寿命と標準偏差を測定しました。平均寿命が 2000 時間、標準偏差が 300 時間であるとき、母平均の 95% 信頼区間を求めなさい。ただし、サンプルサイズは十分大きいと考えます。

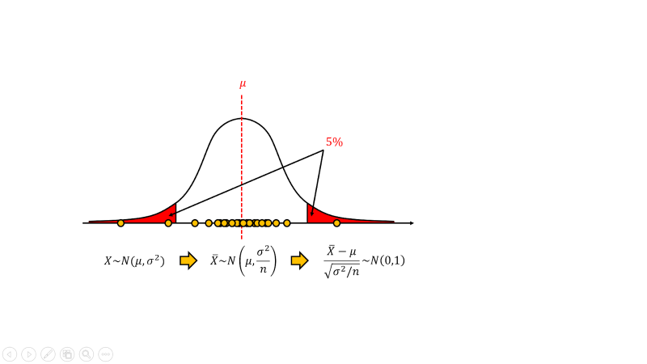
このような場合、標本平均は正規分布に従っていると考えることができ、このことから母平均\(\mu\)の95％信頼区間は
\begin{align*}
2000-1.96\times \frac{300}{\sqrt{40}}\leq \mu \leq 2000+1.96\times \frac{300}{\sqrt{40}}
\end{align*}

で計算することができます。本セミナーでは、上記の推定区間の算出方法やその応用として、必要なサンプルサイズを逆算する方法もご紹介します。

②相関係数の計算と単回帰モデルの数学的な理解

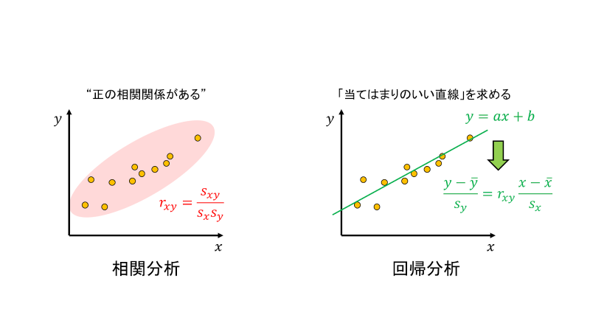
２つ数量データの関係性を可視化するのに散布図が使われます。また、データの平面的な配置に直線的な関係があるとき、「相関関係がある」と表現します。こうした相関関係の強弱を測るのに「相関係数」を用います。本セミナーでは、相関係数の性質は導出の仕方を１からお話しし、さらに、散布図における「当てはまりのいい直線」を具体的に求める「回帰分析」の基礎まで解説いたします。

上記のような、初学者がつまずきやすい点も講義内で丁寧にフォローし、具体例や演習を通じて理解を深めます。独学で学んできた方にも「点と点がつながった」と実感していただけるはずです。これからのデータ活用時代に備え、基礎から統計学をしっかり身につける機会として、ぜひご参加ください。

よくあるお悩み

• Excel分析は少しできるが「なぜそう言えるのか」を説明できない
• 仮説検定などが“手順の暗記”になってしまっている
• 正規分布・二項分布など、分布の使い分けが腹落ちしていない
• 生成AIで統計学をやっているだけで中身を把握してない

研修・講座のゴール

• 数理統計の土台（確率・分布・推定の考え方）を一つの流れとして理解する
• 統計的仮説検定を「意味」として説明できるようになる
• 相関係数・単回帰を、式の意味から語れるようになる
• 統計手法を選ぶ理由を自分の言葉で整理できるようになる

監修・講師のこだわりポイント

「今だったら統計学も生成AIで簡単に分析できるでしょ？」とよく言われます。しかし、それ、本当に合っていますか？実は、間違っていることもあります。また、意味を喋れますか？意味がわからないのになぜそれを信じることができるのでしょうか？「統計をツール任せにしない力」を最短で身につけてもらう構成にしています。統計学は「データをどう読むか」を考える学問ですが、その根底には必ず数学的な裏付けがあります。例えば、単に「平均」や「標準偏差」を求めるだけなら計算は容易ですが、それらの数式が何を意味し、なぜその形になるのかを理解していないと、データの本質を見誤る危険性があります。グラフや分析結果を出すだけではなく、“なぜその結論が言えるのか”を説明できることが、データ活用の現場では差になります。初学者でも安心して、統計を“理解して使える”状態へ進める基礎講座です。

ダウンロード可能な講義資料と演習問題

講義で配布する資料は、すべてダウンロード可能です。講義内で演習時間を確保していますので、手を動かしながら学ぶことをおススメします。

1年間学べる復習動画

講義の動画は録画し1年間公開いたしますので、いつでも復習ができるシステムとなっております。途中出席・退席や欠席されたとしても動画で学習することができますのでご安心ください。