数学が苦手でも、仕事や身近な技術と結びつけながら学び直せる大学数学入門講座です。

「学生時代に数学から距離を置いてしまった」

「大学数学は難しそうで手が出ない」

そんな思いを抱えたまま、大人になってから数学に触れる機会を失っていませんか。一方で、AIやデータ分析、画像処理といった言葉を目にするたびに、その裏側にある数学に興味を持ったことがある方も多いはずです。

本セミナーは、線形代数という大学数学の中でも実用性の高い分野を、基礎から丁寧に学ぶための講座です。行列やベクトルといった概念を、単なる計算としてではなく、図や具体例を通して直感的に理解していきます。

数式に苦手意識がある方でも、理論が何を意味しているのかを実感しながら進められる構成です。線形代数の本質は、複雑な現象を「構造」として捉え、整理し、扱いやすい形に変換することにあります。人口の推移を行列で表して将来を予測したり、回帰分析によってデータの傾向を読み取ったりする例を通じて、数学が現代社会の技術や意思決定とどのようにつながっているのかを学びます。

この理解は、データや情報を論理的に捉える力として、仕事や日常の問題解決にも効いてきます。数学を「解けるかどうか」ではなく、「使って考える道具」として再発見していきましょう。

線形代数とは

線形代数は、大学数学の中でも実用性の高い分野のひとつです。行列やベクトルといった概念は、一見難しく思えるかもしれませんが、実は現代社会のさまざまな場面で活用されています。例えば、3Dゲームや画像処理、AIやデータサイエンスなど、私たちの身の回りの技術の多くが線形代数の原理に基づいています。

セミナー概要

線形代数の基礎から応用までを、具体的な例を交えながら全4回で学ぶセミナーです。行列やベクトルの基本計算から始め、人口予測や回帰分析といった実社会での応用までを扱います。数学に苦手意識のある方でも理解しやすいよう、図や具体例を用いて直感的な理解を重視した進め方が特徴です。大学数学を学び直しながら、現代の技術やデータ分析とのつながりを実感できる内容です。実社会での応用例として、データ分析や機械学習において線形代数がどのように使われているのかを具体的に紹介し、数学がどのように現代の技術と結びついているのかを実感していただきます。
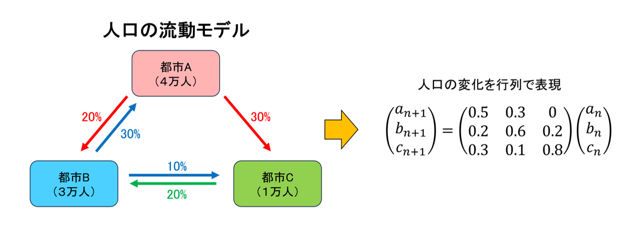
① 人口予測への応用
各都市における人口の推移を、行列を使ってモデル化することができます。こうしたモデルや行列計算から３年後や４年後の人口予測を行うことができます。

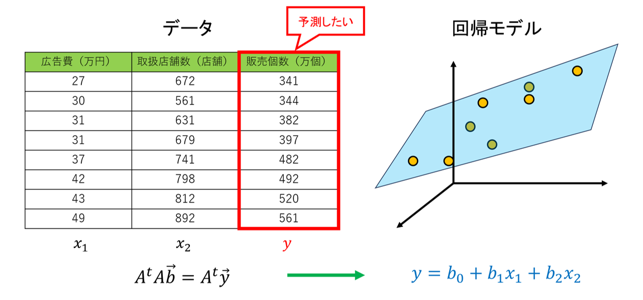
② 線形代数と回帰分析
データを予測する分析手法の１つに回帰分析があります。この方法は誤差（ギャップ）を最小にするという考え方により、行列の基本的な計算に落とし込むことができます。

「数学は学生時代に遠ざかっていた」「専門的な知識がなくても大丈夫？」と不安に思われるかもしれませんが、ご安心ください。本セミナーは、数学に苦手意識のある方や初心者の方にも理解しやすいように、丁寧に解説していきます。

よくあるお悩み

• 線形代数を基礎から学びたい
• 大学数学は難しそうで、自分に理解できるか不安
• 仕事に活かせる数学を知りたい

研修・講座のゴール

• 線形代数の基礎概念を直感的に理解できるようになる
• 行列やベクトルが実社会でどう使われているかを理解する
• 人口予測や回帰分析と数学の関係を知る

監修・講師のこだわりポイント

今、流行の人工知能は線形代数がベースとなっています。まさに、これからの時代、線形代数を知っているかが理系かどうかを決めるといっても過言ではないでしょう。

理系とは、計算の速さではありません。情報を行列で整理し、構造として捉え直す視点のことです。本セミナーでは公式暗記ではなく、なぜその操作をするのかを手を動かしながら体感し、世界の見え方が変わる面白さまでご案内します。

ダウンロード可能な講義資料と演習問題

講義で配布する資料は、すべてダウンロード可能です。講義内で演習時間を確保していますので、手を動かしながら学ぶことをおススメします。

1年間学べる復習動画

講義の動画は録画し1年間公開いたしますので、いつでも復習ができるシステムとなっております。途中出席・退席や欠席されたとしても動画で学習することができますのでご安心ください。