こんにちは。和からの数学講師の岡本です。今回は以下のようなボールに対して語っていきたいと思います。

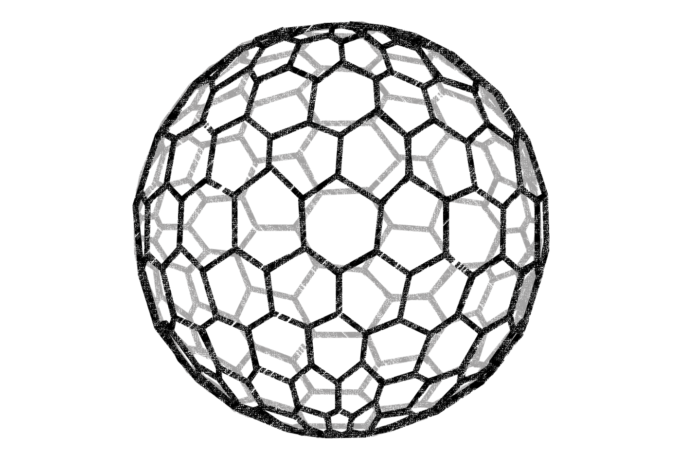
美しいですね！これは「ハニカム構造」と言われる、六角形を規則的に並べた模様（今回は正六角形でなくてもよく、「頂点周りに3つの六角形」という敷き詰め方を考えます）で構成されています。ここでは「ハニカムボール」と呼ぶことにします！ハニカム構造に関しては以前マスログで記事を書いたのでこちらも併せてご覧ください！

ミツバチはすごい！？何かと便利で美しいハニカム構造

１．ハニカムボールは実在するのか？

なにやら不穏なタイトルですが、結論をいうと、実はハニカムボールは存在しません！

つまりハニカム構造を持つ球体は残念ながら存在しないことが数学を使うことで示されます。図に描かれている「ハニカムボール（仮称）」は、実は正確に描かれておらず、実際に図のようなボールを作ろうとすると六角形以外の模様が必要になってきます。こうした「ハニカムボール（仮称）」が存在しえないことはオイラーの多面体定理を用いることで証明できます。

２．オイラーの多面体定理

マスログで何度か登場しているオイラーの多面体定理。例えば、グラフ理論の話でも扱いました。興味のある方はこちらもご覧ください。

路線・ネットワークの数学～グラフ理論への誘い（後編）～

「ハニカムボール（仮称）」は、いわば、ハニカム構造をもつ、多面体と考えることができます。もし、このような多面体が存在していたとすると、オイラーの多面体定理より、頂点と辺、面の数の関係が定理のように決まるはずです。例えば「ハニカムボール（仮称）」頂点の数を\(V\)、辺の数を\(E\)、面の数を\(F\)とします。

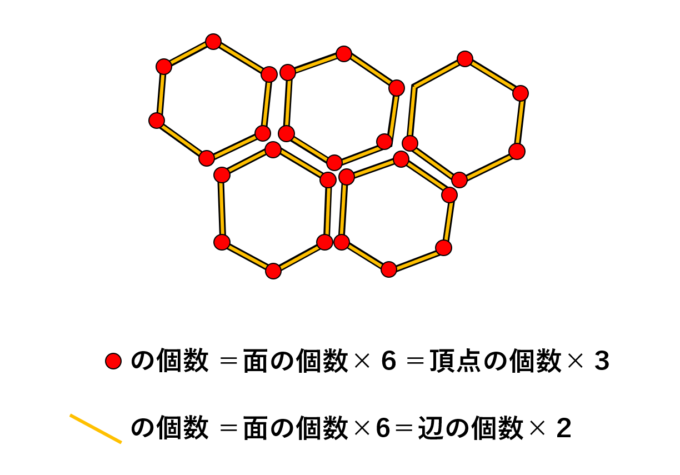
このとき、ハニカム構造であることから、上の図のように、一つの頂点に対して、3つの面が、1つの辺に対して2つの面が重なります。つまり、6個の頂点を持つ面\(F\)個における頂点の総数は3回ダブった頂点の数と一致するので

\begin{align*}
6F=3V\Longleftrightarrow 2F=V
\end{align*}

となります。同様に、6個の辺を持つ面\(F\)個における辺の総数と2回ダブった辺の本数が一致することから

\begin{align*}
6F=2E\Longleftrightarrow 3F=E
\end{align*}

も成り立ちます。このとき、オイラーの多面体定理の式を考えると

\begin{align*}
F-E+V=F-3F+2F=0
\end{align*}

となり、多面体定理の条件を満たしません！このことから、「ハニカムボール（仮称）」は存在しえないことがわかりました。

３．ハニカム構造を保持した立体

オイラーの多面体定理で現れる「２」という数字は、オイラー標数と言われ、より一般的な定理が知られています。

先ほどの「ハニカムボール（仮称）」のような多面体は穴の数が0なので、オイラー標数は\(2\)となっています。例えば、穴が１つ開いたドーナツ型の図形の場合、オイラー標数は\(2-2=0\)となります。ここで先ほどの考察を思い出してみましょう。もし、ハニカム構造を保持した立体があるのだとしたら、\(F-E+V=0\)となってしまい「球体（穴の数0）」ではあり得なかったのですが、穴の数1の立体ならあり得るのではないでしょうか！

実際に、\(F-E+V=0\)だからと言ってドーナツ型の多面体（トーラスと呼びます）が実現可能なわけではないですが、ハニカム構造の場合、なんと実現可能なのです！
トーラスは、長方形（平面）の縦のペアと横のペアを同一視することで構成する方法があります（詳しくは以下のマスログを参照してください）。

ゲームの世界は丸いのか？～RPGから見るトポロジーの風景～

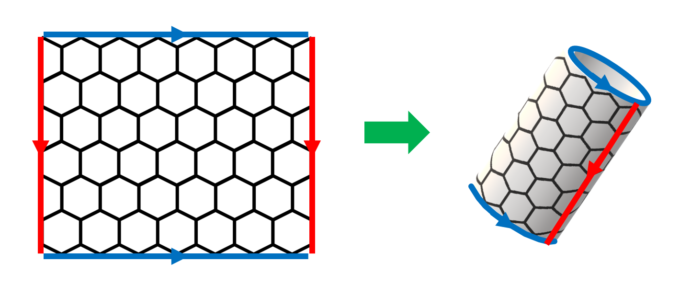
これを踏まえると最初から、平面にハニカム構造を作っておき、これを縦のペア、横のペアで同一視すれば、次の図のような“ハニカムトーラス”が実現できます！

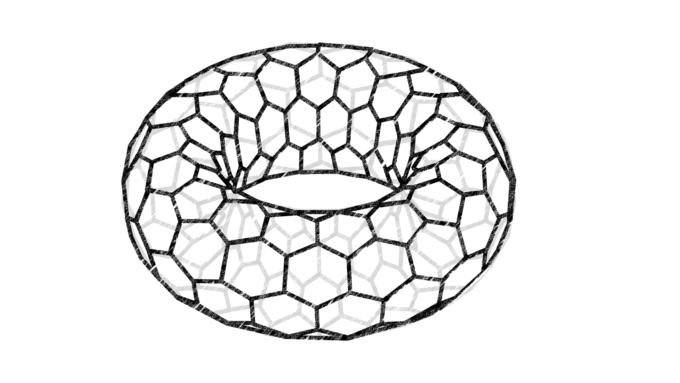
４．さいごに

いかがでしたでしょうか？今回は六角形の構造や美しい多面体に関する話題でした。特に、多面体にはオイラー標数という条件が存在し、メッシュ構造はある程度制限されることがわかります。このような、図形やデザインと数学には深い関係があり、面白い話はたくさんあります。こうした事実を知ることや学ぶことの積み重ねは必ず人生を豊かにすると個人的には思っています。

和からでは、数学的なデザインや、模様に関するセミナーも開催しています。興味のある方は是非無料セミナーへお越しください！

数学的デザイン超入門

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>