こんにちは。和からの数学講師の岡本です。今回は前回に引き続き、グラフ理論についての話題です。前回の内容はこちらからご覧いただけます。

路線・ネットワークの数学～グラフ理論への誘い（前編）～

１．問題の確認

　さて、以下の問題を考えます。

そして前回の記事ではこの問題を「グラフ理論」の言葉で置き換えました。

今回はこの問題を解決していきます。

２．結論

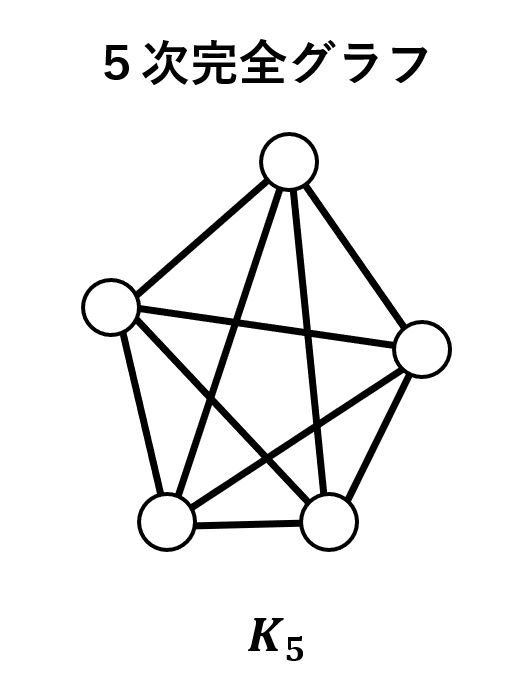
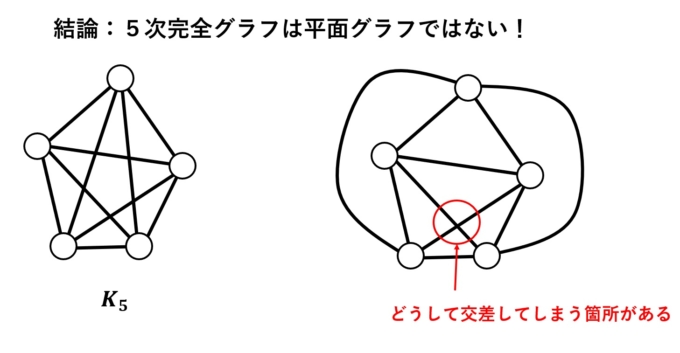
先に結論を述べます。実は５次完全グラフ\(K_5\)は平面グラフではありません。つまり、最初に提起した問題にある条件を満たす道路は「できない」と否定的な回答となります。
数学って面白いですね！このようなできるかできないかをグラフという「つながりの構造」のみに注目することで解決できるのです。

仕方ないので、交差点を作るか、橋またはトンネルを作ることで、道路をくぐらせるしか方法がありません！。

３．証明Step１「オイラーの多面体定理」

では、どうやって証明できるのか。ここからは証明の話をしていきます。実はこの問題を解くにあたって２つのステップを踏むことが必要となります。まず最初のステップとして、「オイラーの多面体定理」を扱います。ここで現れる「オイラー」とはあの”伝説の数学者”「レオンハルト・オイラー」です。彼にまつわる記事は過去に何度かマスログで紹介していますので、興味のある方はこちらをご覧ください。

数学の現人神（アラヒトガミ）の一人、レオンハルト・オイラー 一体何がすごいのか

感銘を受けた数学「オイラーの五角数定理」

では、「オイラーの多面体定理」について解説します。

この定理の美しさにはいつも魅了されます・・・！実際に適当な多面体を考えてみましょう。たとえば、四面体とテキトーな多面体を考えてみましょう。

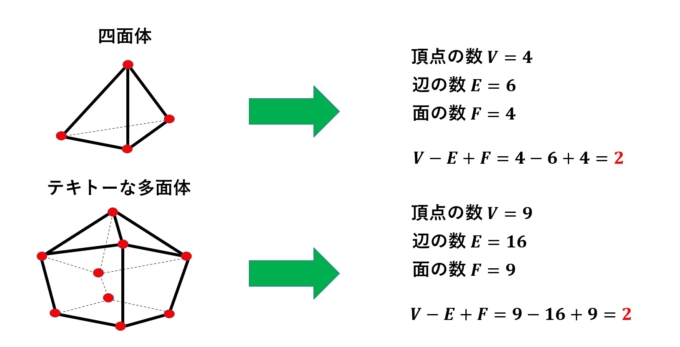
確かに\(V-E+F=2\)となっています！！！畏れすら感じます。

　さて、この定理、なぜ今回の証明に必要なのかというと、グラフが平面グラフであること、この等式が成り立つことが同値だからです！例えば、多面体の面の部分を無視することで、「グラフ」が出来上がります。そして、適当な面の部分を図のように広げてあげることで、平面グラフになります。逆に平面グラフであれば「球面上のグラフ」となり、面をつけることで、多面体になります。

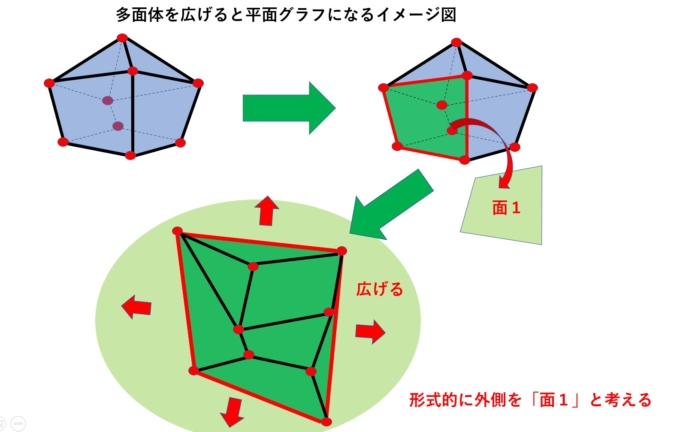
　もう少し正確にお話しましょう。平面に埋め込まれたグラフについて以下のような考察ができます。

・各面は３つ以上の辺で囲まれている

・各辺は２つの面に挟まれている

つまり、「各面を囲む辺の数(\(3F\))\(\leq\)各面に接している辺の数（\(2E\)）」が成り立つ。これにより

\begin{align*}6=3(V-E+F)\leq3(V-E)+2E=3V-E\end{align*}

が平面グラフに対して成り立つことがわかりました。

４．証明Step2「背理法」

次に、５次完全グラフ\(K_5\)が平面グラフであると仮定します。このとき、\(K_5\)は平面に埋め込まれるので、先ほどの考察から

\begin{align*}6\leq3V-E\end{align*}

という不等式を満たすはずです。しかし、完全グラフ\(K_5\)の頂点数はV=5、辺の数はE=10なので、\(15-10=5\leq6\)となり、上の不等式を満足しません。従って、「矛盾」が生じてしまい、これは最初に仮定した「5次完全グラフ\(K_5\)が平面グラフである」ということが原因とみなせ、

「5次完全グラフ\(K_5\)は平面グラフでない」

ということが結論付けられます。このような証明方法を「背理法」といい、数学のあらゆる場面で登場し、証明の決定打になることが多いです。

５．さいごに

いかがでしたでしょうか？今回は路線の問題を「グラフ理論」を使って解決してみました。グラフ理論は比較的新しい数学の分野ですが、現代社会の様々な箇所で応用されています。また機会があればグラフ理論の応用について解説していきたいと思います。

また、今回のグラフ理論に関しては「グラフ理論序説（プレアデス出版）」がおすすめです。グラフ理論の基本的な内容から様々な応用まで非常にまとまってあります。なお著者の仁平政一先生は和の講師として活躍されています。

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>