Excelを使った素数アート-ガウス素数前編-
公開日
2020年11月3日
更新日
2020年11月3日

こんにちは。和からの数学講師の岡本です。以前マスログで、Excelを使った“素数アート”として「ウラムの螺旋」というものをご紹介しました。
その際にExcelで「素数の判定」という呪文を使いました(Excel 365のみ対応の関数使用)。この素数判定を使って、次のような模様を作成することができます。

これは素数の「2次元版」を描いた模様です。非常に美しいですね!見入ってしまいます!
今回はこの模様についてお話をしていきます。
この記事の主な内容
1.素数とグループ分け
素数とは簡単にいうと、「1と自分自身以外の数で割れない数」のことです。例えば
\begin{align*}2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,\ldots\end{align*}
といった具合です。少し観察すると素数は最初の「2」以外は全て奇数になっていることがわかります(つまり2は“唯一の偶素数”なのです!)。特殊な2以外の素数を4で割ると奇数であることから、必ず「余りが1となるもの」と「余りが3となるもの」の2つのグループに分かれます。
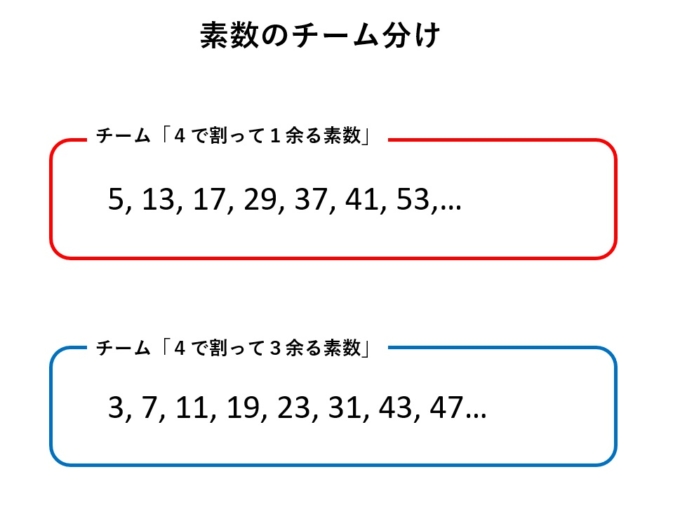
素数が無限に存在することが知られていますが、上の2つのグループ分けを考えたとき、どっちのグループの方が多いでしょうか?もしかすると片方は有限個しかないかもしれません。
しかし、「ディリクレの算術級数定理」という偉大な定理(今回はこの定理には立ち入りません)を使うとどちらも無限に存在することが示されます。数学の世界は奥が広いですね。。。
2.4で割って1余る素数たちの性質
前節のグループ分けの中で、4で割って「余りが1となるもの」のグループに注目します。このグループには実は次のような驚くべき性質があります。
「え!!!?ほんとうですか????」と疑ってしまいたくなりますが、本当です。
例えば、「5」という素数は4で割ると確かに1余ります。そして実際に5は
\begin{align*}5=2^2+1^2\end{align*}
となり、確かに2つの平方数の和で書けています。では、4で割って1余る、41という素数はどうでしょう?
\begin{align*}41=25+16=5^2+4^2\end{align*}
となり、確かに2つの平方数の和で書けています。しかも、定理の主張は「表し方はこの1通りしかない(一意的)」ということまで述べています。素数、恐るべし。。。!
ちなみに「4で割って3余る素数は絶対に2つの平方数の和で表すことができない」ということも証明されています。
なお、特殊な素数2に関しては
\begin{align*}2=1^2+1^2\end{align*}
であることから、「4で割って1余る」グループに所属させておきます。
3.複素数の世界の整数
数学の世界では実数の外側にさらに大きな「複素数」といわれる世界が広がっています。私たちが扱っている「整数」はいわば実数の世界の中に閉じ込められた状態であり、複素数の世界にも「整数」なるものが存在します。
複素数は「2乗して\(-1\)になる虚数単位\(i\)」を使って\(a+bi\)という形で表されます(\(a,b\)は実数)。複素数の世界の整数として、\(a+bi\)(\(a,b\)は整数)というものを考えるのが自然です。
また、実数の世界はこれまで「数直線上」という1次元的な表現に限られていましたが、複素数は2つの実数のペアで表されることから2次元的な表現が可能になります。つまり、複素数は「平面上の点」として考えることができます。
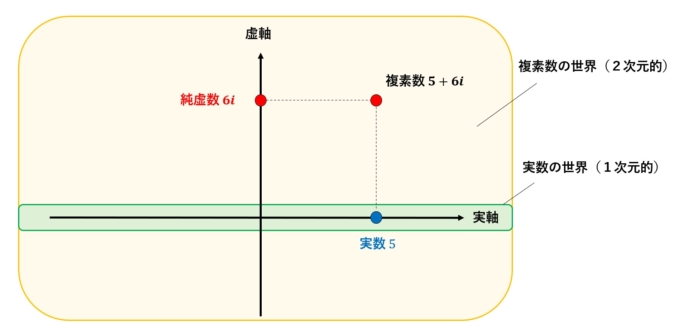
以上の説明をまとめましょう。
・整数は実数という1次元的な世界の点だった。
・複素数の世界は2次元的であり、その世界にも整数という概念がある。
4.さいごに
いかがでしたでしょうか?前編では素数のグループ分けとその驚くべき性質、そして整数を2次元的にとらえるという話をしてきました。そうすると気になるのはやはり「2次元的な素数」についてです!後編ではこのあたりについて詳しく解説していきます。お楽しみに!
和からでは「Excelアート」に関する無料セミナーも開催しております。興味のある方は是非一度ご参加ください!
和からではExcelを使った集計や分析、素数や整数論などの大学数学をご自身のペースで学びたいことを学びたいだけ学ぶことができます。少しでもご興味を持たれた方は是非無料セミナーへのご参加、無料個別カウンセリングのご利用を!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>













