Excelを使った素数アート-ガウス素数後編-
公開日
2020年11月5日
更新日
2020年11月5日

こんにちは。和からの数学講師の岡本です。前回に引き続き、素数の奏でる「幾何学模様」について解説していきます。
この記事の主な内容
1.複素数の世界の素数
さて、素数とは前編で説明した通り、数をどんどん素因数分解していき、これ以上割れないような数のことであり、いわば数の世界の「原子」のようなものです。
しかし、「これ以上割れない」のは、考えている世界が狭いからなのです。数学の世界では実数の外側にさらに大きな「複素数」といわれる世界が広がっています。
複素数に関しては前回少しお話しましたが、この世界にも「整数」に対応するものがあります。その一例として\(a+bi\)型の数(\(a, b\) は整数)という例をご紹介しました。実はこのような複素数を「ガウス整数」と呼びます。
さて、4で割って1余る素数について復習ですが、このような素数は \(p\) は必ず、2つの平方数の和(\(a^2+b^2\))で書けます。このような数を複素数の世界で考えると次のように「無理やり」因数分解できてしまいます。
\begin{align*}p=a^2+b^2=(a+bi)(a-bi)\end{align*}
これはつまり、「4で割って1余る素数は、2つのガウス整数で素因数分解できる」ということを意味します。つまり、4で割って1余る素数はガウス整数の世界では「数の原子」ではないのです!!なお、2も
\begin{align*}2=1^2+1^2=(1+i)(1-i)\end{align*}
となることから2つのガウス整数に分解されてしまいます!実は分解された2つのガウス整数がこの世界における「数の原子」となります。
また、4で割って3余る素数は平方数の和で書けないという事実から、ガウス整数の世界においても「数の原子」であり続けます。
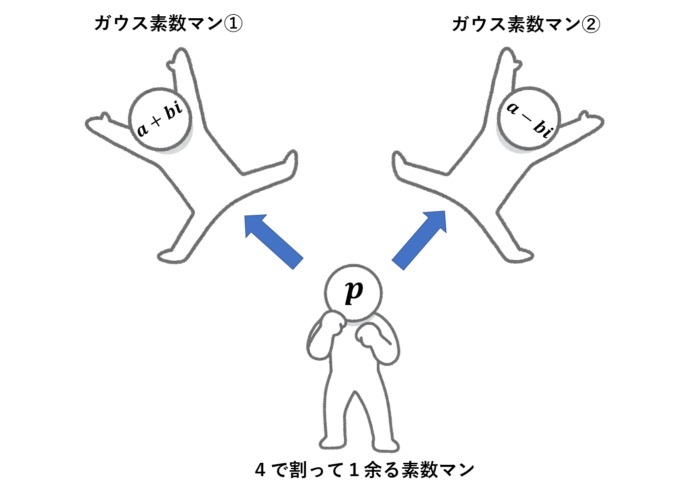
このようなガウス整数の世界の素数のことをガウス素数といいます。
2.ガウス素数の位置の特徴
前節で説明したガウス素数ですが、平面上にその位置を描写すると次のような分布になります。

美しい模様ですね!!まさに素数が奏でる幾何学模様となっています。では、これらのガウス素数がどのように位置しているのかを考えてみましょう。
まず、複素平面内では正の数、負の数とあり、どちらも分解は符号の違いしかないので、左右対称です。そのため、基本的には正の数のみ考えます。
また、実数軸上に乗っている素数は4で割って3余る素数のみで、2と「4で割って1余る素数」は、下の図のように上下に分解されます。
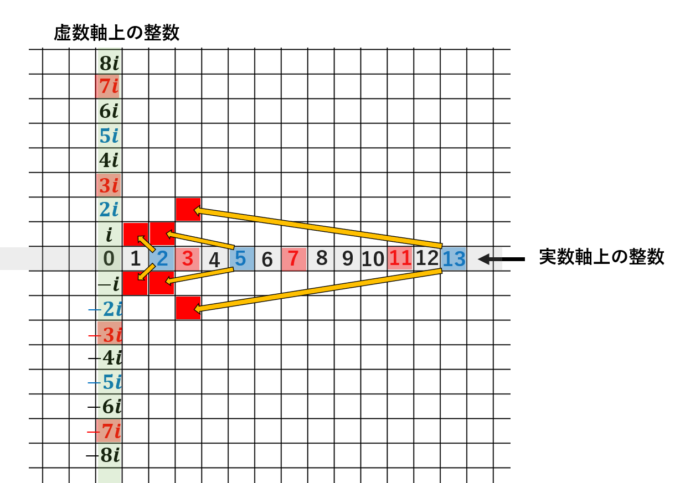
また、純虚数である(4で割って3余る素数×\(i\))もこれ以上分解はできないので、この世界では素数となります(つまりガウス素数)。
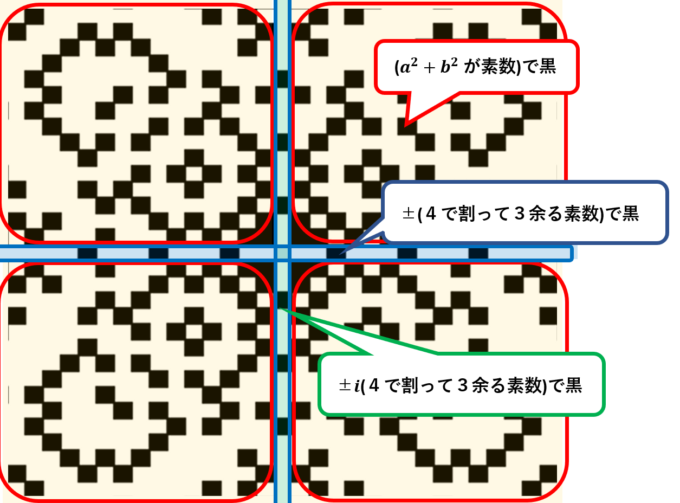
以上を踏まえると、ガウス整\(a+bi\)がどんなときにガウス素数となるのか以下のようにまとめられます。
・\(b=0\)(実数軸上)では\(a\)が4で割って3余る素数のとき
・\(a=0\)(虚数軸上)では\(b\)が4で割って3余る素数のとき
・\(a\neq 0\), \(b\neq 0\)では \(a^2+b^2\)が素数ののとき
3.Excelで描写する
Excelで描写する方法を簡単に解説します。基本的なやり方は「クロス集計」の要領です。
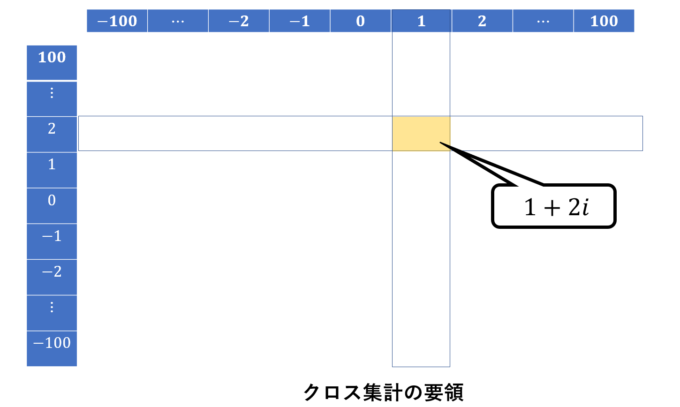
例えば図のように-100から100までの列と行を作ります、こうして、この表の中のセル(1, 2)を複素数\(1+2i\)とします。
そして、前節で説明した「ガウス素数」の特徴をもとに、実数軸、虚数軸、それ以外で分けて考えます。そして主な役割を果たす【選んだセルA1の数値が素数であれば1を、そうでなければ空白を出力する関数】
=IF(A1=2,1,IF(MIN(MOD(A1,SEQUENCE(SQRT(A1),1,2)))=0,””,MIN(MOD(A1,SEQUENCE(SQRT(A1),1,2)))))
と、【選んだセルA1の絶対値が4で割って3余る素数であれば1を、そうでなければ空白を出力する関数】
=IF(OR(MIN(MOD(ABS(A1),SEQUENCE(SQRT(ABS(A1)),1,2)))=0,MOD(ABS(A1),4)=1),” “,MIN(MOD(ABS(A1),SEQUENCE(SQRT(ABS(A1)),1,2))))
を利用して3つのエリアで\(a\)または\(b\)が4で割って3余る素数か、\(a^2+b^2\)が素数かを判定します。(ここでコピー機能を利用するために「相対参照」機能をオススメします。)そしてウラムの螺旋の記事と同様にカラースケールを使うことで、ガウス素数と判定されたセルに色を付けます。
4.さいごに
いかがでしたでしょうか?後編では「2次元的な世界」の素数としてガウス素数というものをご紹介しました。数の世界はまだまだ奥が深く、今回お伝え出来なかった話もたくさんあります。素数や素数の分解法則に関するオススメの書籍として加藤和也先生の本をご紹介いたします。
加藤先生の独特で軽快な言い回しが非常に面白く、深い数学までわかりやすく解説されています。さらに、和からでは今回ご紹介したような「Excelアート」に関する無料セミナーも開催しております。興味のある方は是非一度ご参加ください!
和からではこうしたExcelを使った集計や分析、素数や整数論などの大学数学をご自身のペースで学びたいことを学びたいだけ学ぶことができます。少しでもご興味を持たれた方は是非無料セミナーへのご参加、無料個別カウンセリングのご利用を!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>














