暇な会議で大発見!?素数が描く不思議な模様
公開日
2020年9月20日
更新日
2020年9月20日

こんにちは。和からの数学講師の岡本です。今年はコロナの影響で在宅勤務やリモートワークなど、「働き方」の見直しが広く行われてきました。弊社のセミナーもZoomを使ったオンラインセミナーの導入により、これまでとは違ったニュー・ノーマルが形成されつつあります。そんな中、さまざまな形で会議が進められています。皆さんは会議はお好きですか?一言一句発言者の内容を理解し、違和感があれば質問。常に神経を使うので、会議後というのは少なからず疲れちゃいますよね。さて今回のお話は、退屈な会議中に落書きをしていた数学者のお話です!
この記事の主な内容
1.ウラムという数学者
今回の主役はポーランドの数学者スタニスワフ・マルチン・ウラム(1909-1984)です。

彼は集合論、測度論、トポロジーなど数学の多くの分野で業績を残しているほか、水素爆弾の基本機構の発案者でもあり、「テラー・ウラム配置」と名前が残っています。そんなウラムは、とある研究発表の会議中、非常に「退屈」だったそうで、手元の紙とペンを使って“落書き”を始めました。
2.会議中の発見
彼の“落書き”は次のようなものです。1,2,3と順番に数を渦状に並べます。特にノートのマス目に合うように綺麗に並べていきます(下図参照)。
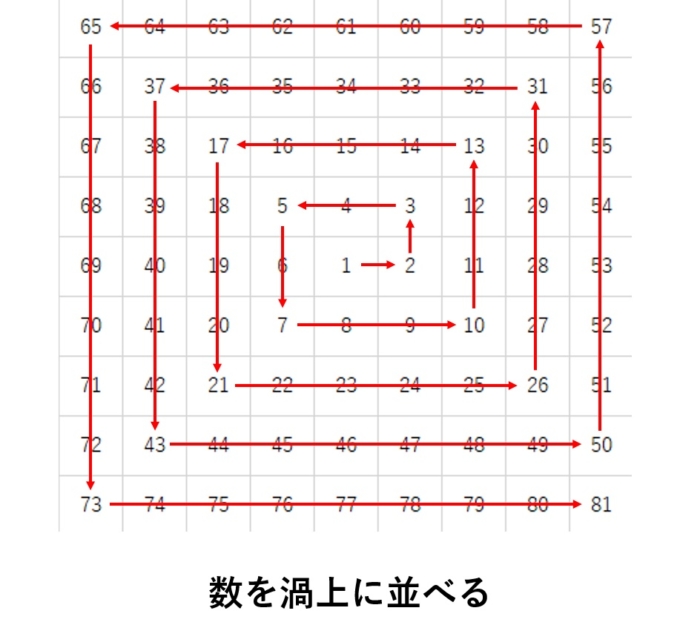
そして、これは数学者の性(さが)なのでしょうか、彼は何を思ったか「素数」の部分をひたすら黒く塗りつぶしていき、模様を作りました。素数とは「1以外で割り切れない数」の事をいいます。ただし1は通常素数とは考えません。つまり、2,3,5,7,11,13,17,19…という具合の数です(数えると落ち着きます)。

するとなんということでしょう。なんだか規則があるようなないような、綺麗な模様が出来上がりました。美しいですね!!

これを発見者ウラムの名前を冠し、「ウラムの螺旋」といいます。縦線や斜め線がうっすら見えます。これは「素数には何かしらの規則があるのではないか」ということを意味します。でたらめに並んでいるように見える素数の世界にも「規律」があるようです。しかし、残念ながらこのウラムの螺旋の構造はいまだ完全には解明されていません。
3.サックスの螺旋
数字の並べ方次第で、さまざまな模様が出来上がります。ウラムの螺旋ではマスに従って渦を描いていましたが、アルキメデスの螺旋という曲線に従って数を並べ、素数に色塗った「サックスの螺旋」というものを知られています。発見者のロバート・サックスの名前にちなんでいます。
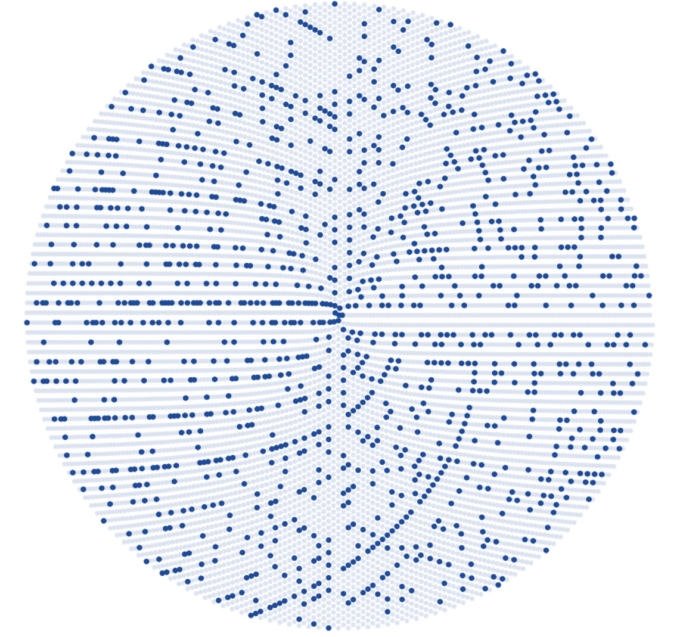
この螺旋もなんだか規則が見え隠れして魅力的ですね!まさに「神秘の模様」です。
4.オイラー素数との関係
ウラムの螺旋に関してもう一つ面白い話題があります。まず、並べた数全てに対して「40」を足します。つまり、渦の始まりを41にするのです。すると、面白いことに、右上がりのラインが綺麗にそろっていきます!不思議ですね!
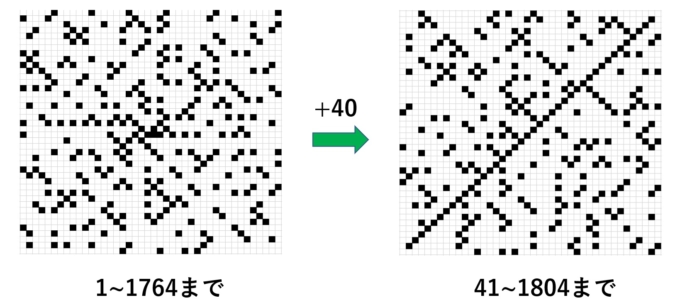
元のウラムの螺旋の右上がりラインの数を注意深くみると、\(n^2+n+1\)の形で表されることがわかります。
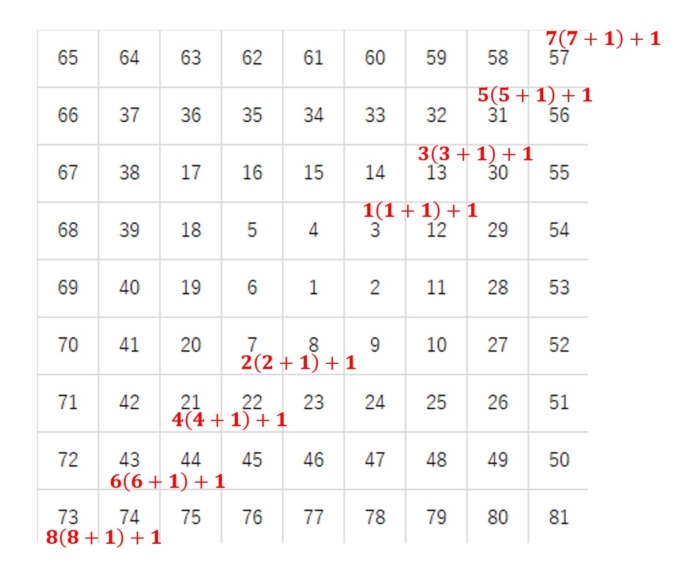
ここに\(40\)を足すことで、右上がりラインの数は「\(n^2+n+41\)」の形で表されます。これは、レオンハルト・オイラーによって考察された、「素数生成関数」です。当時オイラーは、「素数を生み出す(なるべく簡単な)関数はないか」という問題を考えていました。今回のような
\begin{align*}F(x)=x^2+x+41\end{align*}
という、一見何の変哲もない関数ですが、\(F(1)=43\)(素数)、\(F(2)=47\)(素数)、\(F(3)=53\)(素数)…という具合に、実は\(x=39\)まで連続で素数をたたき出します!!このような関数から生み出される素数を「オイラー素数」と呼びます。なぜ1~39までが連続で素数になるのか。実はしっかりとした理由があり、現代の代数的整数論の話まで膨れ上がります。ですので今回は踏み込みませんが、理由があるということだけで十分すごいですよね。
話はそれましたが、とにかく、こうした理由があり、渦の始まりを\(41\)とすると右上がりラインは39個素数が連続で続き、直線模様が浮き上がるのです。
5.さいごに
今回、ウラムの螺旋はなんとExcelを使って描きました。工夫をすれば以外にも簡単に描けます。
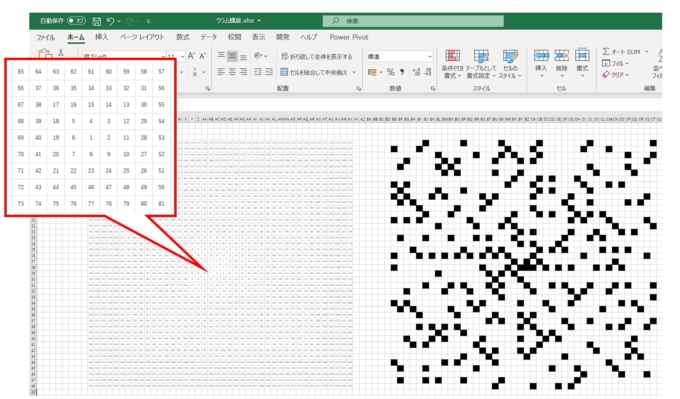
さらに、全体に\(40\)足すことによって、自動で模様が変わる仕組みになっているため、今回のような模様も難なく描けました。Excelでの描き方に関しては次回取り上げてみようと思います。
和からでは数学にまつわる様々なデザインやExcelアートに関する無料セミナーを開催しております!興味のある方は是非一度ご参加ください!
またご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。
<文/岡本健太郎>














