こんにちは。和からの数学講師の岡本です。今回は「路線設計」の問題をグラフ理論の言葉で置き換える話をします。以前「グラフ理論」に関連する記事を書いたので、こちらも併せてご覧ください。

一筆書きの数学からモノクロデザインへ

先手必勝！？戦略とゲーム理論（中級編）

次の問題を考えます。

１．単純な例を考える（３つの街の場合）

　このような複雑そうな問題はまず具体例を考えてみます。そこで、比較的イメージしやすそうな３つの場合について考察します。

３つの街の場合、単純に全ての街を以下のようにつなぐことで、条件は全て満たされます。

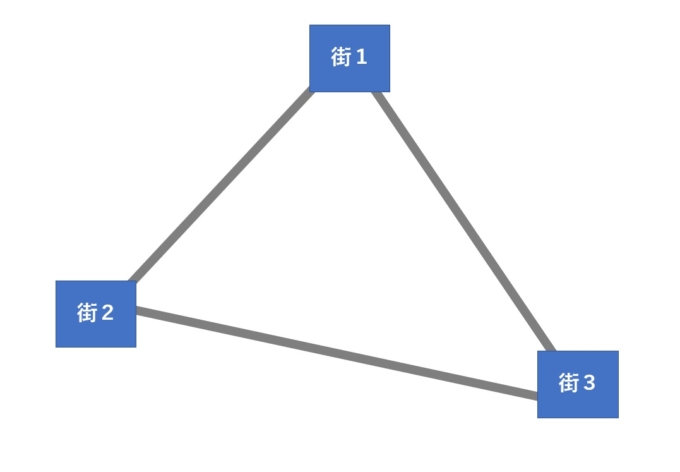
２．単純な例を考える（４つの街の場合）

次に、４つの街の場合を考えましょう。まず、単純に全ての街をつなぐことで、以下のような路線ができます。

しかしながら、このような設計では真ん中に交差点が必要になってしまいます。
そこで、対角線の道路を以下の図のように「外側にまわす」ことで、(Ⅰ),(Ⅱ)の条件を満たす路線が完成します。

３．グラフ理論の導入

複雑な場合でも統一的かつ簡潔に表現するために「グラフ」という概念を導入します。
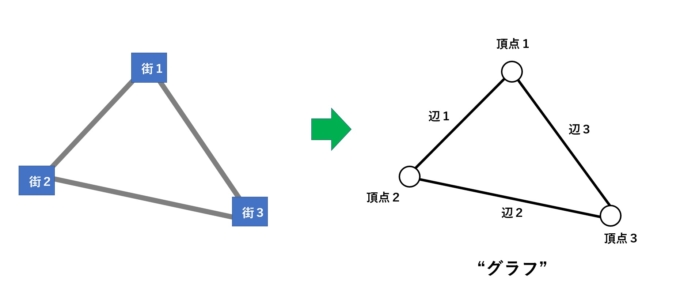
街に対応するものを「頂点(vertex)」、道路に対応するものを「辺(edge)」と呼ぶことにします。上で考えた「路線」とは、「頂点と辺のつながりを表す図形」とみなすことができ、数学の世界ではこれを「グラフ(graph)」と呼びます。

また、\(n\)個の頂点全てを結んでできるグラフのことを「\(n\)次完全グラフ」と呼び、\(K_n\)と書きます。そして、頂点以外の点で、辺が交差しないように平面に描けるグラフのことを「平面グラフ」と呼びます。

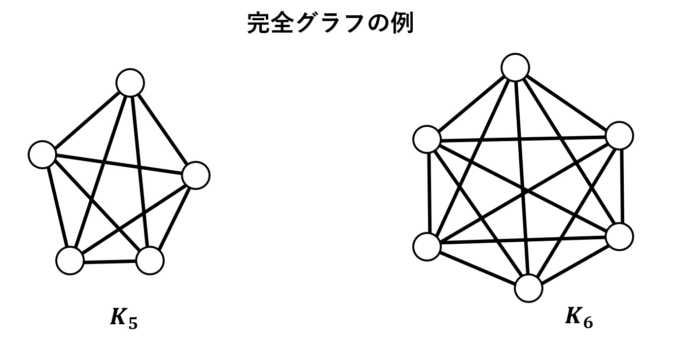
　今回の条件(Ⅰ)はグラフ理論の言葉では「街をつなぐ路線が完全グラフである」と表現でき、条件(Ⅱ)は「街をつなぐ路線が平面グラフである」ことを意味しています。
　なお、街が３つ、４つの場合のグラフは「完全グラフかつ平面グラフ」であり、今回の問題はグラフ理論的に以下のように書き換えることができます。

グラフとは「頂点とそのつながりの情報そのもの」であり、実際は「上を通る」「下を通る」「交差点」などは関係ありません。この意味で「路線（道路）」と「ネットワーク」に違いがあわれます。グラフ理論に近い対象はどちらかというと「ネットワーク」です。「平面グラフ」という概念を持ってくることにより、物理的な「路線（道路）」のモデルをグラフ理論で考えることができるのです。

４．さいごに

いかがでしたでしょうか？今回は路線の問題を「グラフ理論」を使って表現してみました。
しかし、まだ問題に対する回答は得られていません。次回はグラフ理論を使って、5つの街に条件(Ⅰ),(Ⅱ)を満たす道路が作れるかどうかの結論を出します！しかもその議論の中では大数学者レオンハルト・オイラーの名前も登場します！（オイラーに関する記事はこちら↓）

数学の現人神（アラヒトガミ）の一人、レオンハルト・オイラー 一体何がすごいのか

後編はこちら！

路線・ネットワークの数学～グラフ理論への誘い（後編）～

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>