こんにちは。和からの山田です。和からでは統計学の個別指導を行っています。

人が行う何らかの経営的意思決定。事業拠点を増やすかどうか、新しい販促手法を導入するのか、その際に求められる有効な情報とはどんなものでしょう？意思決定により選択された事柄はこれから起きることです。例えばAを選択すればこれだけの収益が得られるというだけでなく、その確実性の程度、確率が示されればより有効でしょう。

先日SF映画を見ているとこんな場面がありました。ロボットが「勝てる確率は13％」と、とても危険な状況にあることを周囲に伝えます。ロボットは能力差だけでなく過去のデータから偶然の要素を含めて13％という確率を計算したのでしょう。未来のヒロインはこれを聞いて決意します。「13％もある。もう逃げない」と言って最後の決戦に向かってゆきます。最後に決断するのは人です。ここで注目したいのは確率を伴う予測は意思決定を助けるだけでなく、その意図を明確にし、同じ認識を情報共有させることです。

ところでこんなロボットを傍に置いておきたいと思いませんか？

こんな要望に応えられるのが「STAN」です。STANは2012年に公開され、日本でも書籍の形で4～5年前より紹介されてきています。しかしプログラミング言語の記述が必要なことや、確率や統計の基礎知識を有している人向けであったりするため、統計に縁がない人には「STAN」を知る機会は限られてしまっています。そこでこの場を利用して「STAN(注)」を使った簡単な分析例を紹介して特徴の一つ、予測値が確率分布の形で得られることを知って頂ければと思います。

分析例：ミニトマト栽培の新手法を評価し、導入の可否を決めよう！

　
ある農家ではすでに何年もミニトマトを栽培していますが、収穫量はあまり芳しくありません。そんな農家がミニトマトの新手法を試しました。過去の平均的な一株当たりの収穫量は2,000gですが、新手法により600gの増加を期待しています。一粒平均19gですから約30粒、一房10粒ですから鈴なり3房の増加を目指しています。

600gの増加の確率が70％あれば、経費は増加しますが申し分ないと考えています。一方増加量が200g以下であれば問題外で新手法の導入は諦める予定です。

15株で新手法を試み以下の収穫を得ることができました。
2,260 2,617 2,810 1,987 2,653 2,671 2,412 2,419
2,415 2,336 2,435 2,310 2,364 2,565 2,780 (g)

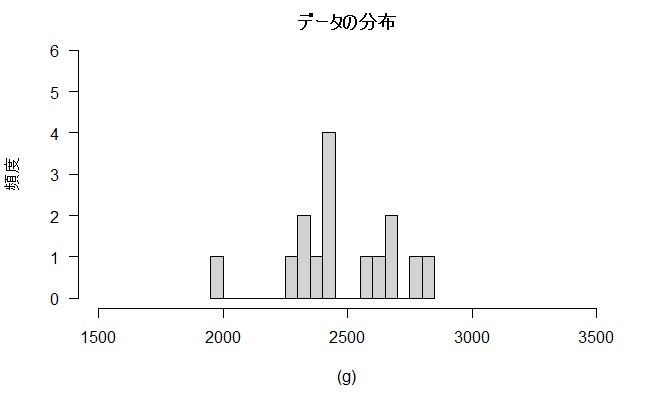
目標の2,600gを超えたのは5株、平均2,470gでまずまずです。大雑把なご主人は過去平均2,000gを大きく上回ったことからもう来年は新手法で栽培すると言っています。しかし、目標には少し届かない様子ですから安心して新手法の導入とはいきません。慎重なおかみさんは「STAN」を利用して新手法を詳しく評価することにしました。

おかみさんは経験からミニトマト一株当たりの収穫量は正規分布に従うと考えています。正規分布は平均を真ん中として左右均等に離れるほど起こりにくくなる確率分布です。例えば人の身長も正規分布するとされますが、体重は環境や嗜好に左右されることが多く正規分布には従いません。

正規分布の位置や形状を決める要素、つまりパラメータは平均と標準偏差の2つです。標準偏差はばらつきの大きさを表します。ミニトマトでは株ごとの収穫量の違いのことです。ばらつきの要因は株の遺伝的個体差やたまたま植えられた場所の水分や土質、光、その他害虫など環境差です。

手法の概要

実際の分析評価に進む前に「STAN」のベースとなるベイズ統計と伝統的統計手法との違いを確認しておきましょう。その違いこそが分布の形で予測値が得られる背景となっています。

ベイズ統計

ベイズ統計ではデータの分布や過去の知見などからまずデータの背景にある確率モデルを仮定します。今回の場合はおかみさんの言っている正規分布が確率モデルとなります。但し仮定したモデルにより重要な特性を見落とす結果となっていないか、分析結果や今後のデータに注意を払ってゆくことが必要です。本当は正規分布ではなくて山が二つ、あるいは右下がりの台形状の分布かも知れません。

モデルの仮定後はモデルの形を明らかにするためにパラメータを推定する作業に進みます。今回は15株のデータから二つのパラメータを推定しますが、データの位置づけや推定方法が従来の統計手法とはだいぶ異なります。

ベイズ統計においてデータは、未知のパラメータを推定する上で確定した条件として捉えます。推定方法はパラメータのサンプルを乱数として連続的に発生させ、その中からデータが出現する確率の高いサンプルを最初取捨選択します。そして乱数の発生が進むにつれ安定的に有効なパラメータを発生させる仕組みとなっています。

データが出現する確率の高いところのパラメータサンプルは数多く、出現確率の低いところのパラメータサンプルもそこそこに、確率に比例して発生してゆきます。得られたパラメータサンプルを集積すればパラメータの確率分布を得ることができます。

また、今回パラメータは平均と標準偏差の2つですが同時分布のパラメータとしてペアで発生します。その為データの中心から離れた平均パラメータの場合、ペアで発生する標準偏差は大きな値となります。今回の事例で見てみると平均と標準偏差のパラメータ平均値はそれぞれ2,469gと242gです。2,700g以上の大きな平均パラメータサンプルは7個ありますが、ペアで発生した標準偏差パラメータの平均は403gです。また、2,200g以下の小さな平均パラメータは1個ですがペアで発生した標準偏差パラメータは444gで大きな値となっています。事例の際のパラメータ分布で位置を確認してみてください。

パラメータサンプルを生成する方法はMCMC(マルコフ連鎖モンテカルロ法)と呼ばれます。その中でもさらにいろいろ方式があるのですが、STANの利用する方式は最も無駄なく有効サンプルを得ることができるとされています。ちなみにソフトの名称STAN(スタン)はMCMCを考案した数学者スタニスワフ・マルチン・ウラムの頭文字からとったものです。

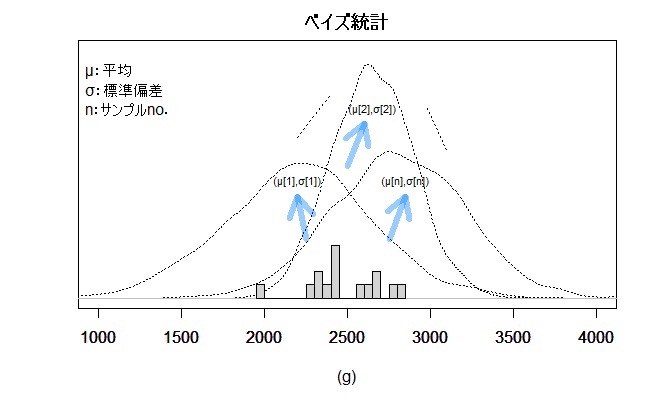
予測は逆に、同時に得られたパラメータの確率モデルから予測値を無作為に乱数として発生させます。各パラメータのペアから１個の予測値を発生させ、それを集積すれば予測分布となります。予測値の発生はSTANでもR でもできます。

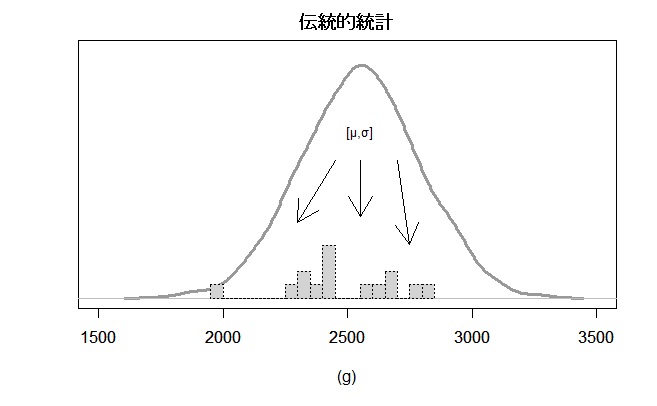
伝統的統計

伝統的統計は新技術の効果の有無などの評価を中心に展開されてきました。ベイズ統計とは逆にある確定したパラメータを持つ母集団からサンプルデータが発生したと考えます。どんな確率分布から得られたデータも標本平均は正規分布に収束するという定理など利用してパラメータを推定します。平均や標準偏差の信頼区間は統計用の分布関数を利用して計算で求めますが、90%信頼区間とは 100 回標本を取り直して 90 回は真の平均がこの範囲に含まれることを意味します。平均や標準偏差について～以上は何％という確率を求めることができます。この確率を用いて有意性検定が行われますが、平均や標準偏差の分布図を描くことはできません。予測値は確率モデルを仮定をした上で平均のような代表値を使って求めることはできます。しかし、「STAN]で行うようなばらつきを含むパラメータによる予測はできません。

今回の事例で伝統的統計による平均の信頼区間は次のようになります。平均は2,469 ｇ、90%信頼区間は2,370g～2,568gです。後で出てくる90％ベイズ信頼区間と比較して頂きたいのですが、ほぼ一致しています。全く異なるアプローチをしてこんなに一致することに驚きます。但し、10サンプル、5サンプルとデータ数が小さくなるとベイズ信頼区間の範囲の方が少し広くなってきます。

ミニトマトの事例への活用

それではミニトマトの事例に戻りましょう。

パラメータの推定

15株のデータからパラメータを推定を行います。MCMCサンプルを今回5,000個発生させました。時間は3秒足らずです。サンプル数を増やせば、毎回のサンプルによる変動は小さくなりますが今回の単純なモデルなので5,000個で推定しています。

まずは平均の分布を見てみましょう。

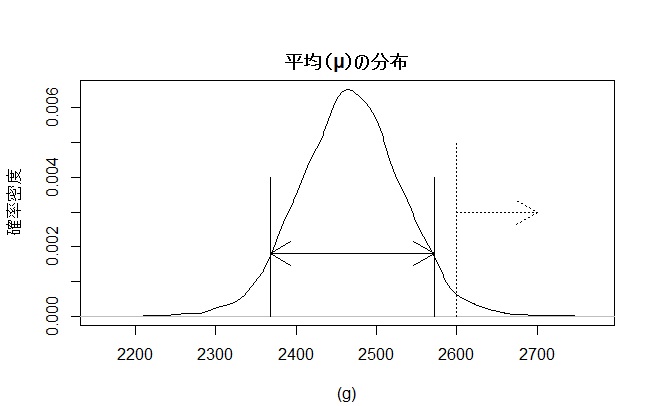
平均は2,469g、90%ベイズ信頼区間は2,368g～2,572gで従来より400～600g近く上回っていますが、目標の2,600gを超える確率はわずか2.1％です。目標の2,600gが70%はとても難しい様子です。
次に標準偏差の分布を見てみましょう。

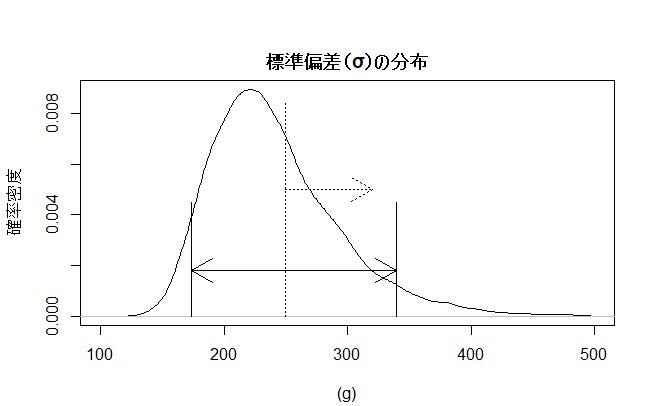
標準偏差はばらつきの大きさですのですべて正の値となっています。中央値は233gで新手法は細かい管理を行う分、従来法に比べるとばらつきは小さくなっているようです。しかし正の方向に伸びており平均は242g、90％、信頼区間は約170g～340g となります。平均収穫量の10％に相当する250 ｇ以上の確率は36.2％あります。予測収穫量は平均値から標準偏差2つ分、250g とすると2倍して500g以上の範囲で増減すると考えられます。

おかみさんはいきなり従来比30％増の2600g を基準にするのではなく、本当は20％増の 2400g で評価したいと思っています。改善点が多々あり 2400g 以上の収穫が約2/3、65％以上見込めれば新手法でOKと考えています。ペアで得られたパラメータサンプル（平均と標準偏差）は個々正規分布を確定しています。おかみさんはまず2400g 以上の確率を個々で求め、確率分布にしました。

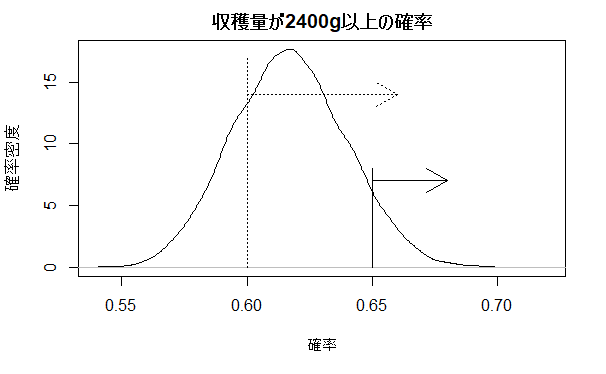
2400g以上の確率の平均は 61.7％で65％をやや下回ります。確率65％以上の見込みは約7％と小さいですが、60％以上の見込みは約77％あります。おかみさんは予測値で全体の様子を見てさらに検討してゆくことにしました。予測値は各収穫量の平均確率（2400gでは61.7％）による分布となります。

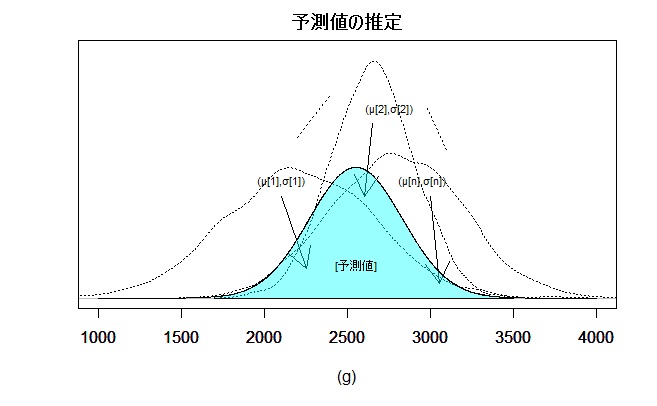
予測値の推定

同時分布で得られた平均と標準偏差を使って１個ずつ、計5,000個の予測値を発生させ集計して予測分布を作ります。

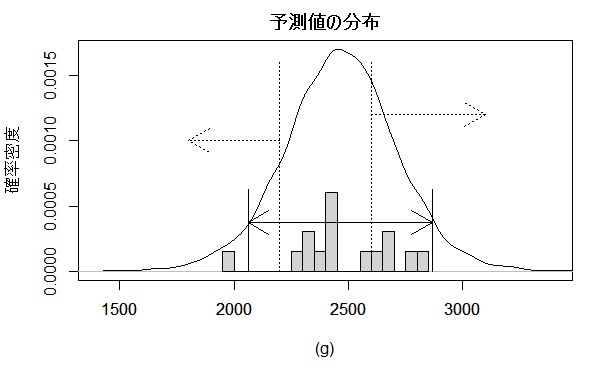
予測値の平均は約2,470g、90%信頼区間は約2,040g～2,890gで従来の目安である2,000gを信頼区間は上回っています。2,000gに対して増加量が200g以下の可能性は13.8%、一方600g以上の増加の可能性は29.6％予想されます。600g以上増加は30％とだいぶありますが、一方200g以下も10％強で収穫量の幅は大きいです。

おかみさんは収穫量の差の原因を苗の段階から見直しを条件にして、ご主人の考えに賛成しようかと考え始めています。

以上で分析例は終わりです。

確率を含む予測値による意思決定、結果の表現について特別難しい用語もなく、フツーと感じて頂ければよいのですが。いろいろなアイデアや経験を持った人が確率分布の同じ図を見て各々の視点で評価する。そんなイメージを懐いて頂けたらと思います。

今回は評価対象のデータだけでしたが比較対象の従来法のデータもあればさらに有益な予測値による評価が可能となります。重回帰分析においても条件ごとの予測値が分布の形で得られます。またの機会にご紹介できればと思います。

おまけ(よくいただく質問)

質問:プログラム言語の学習には時間がかかるのでしょうか？

ミニトマトのような単純なモデルであればSTANのコードは10行足らずです。データ、パラメータ、モデルはそれぞれ何かを書けばよいだけです。多くても30行です。それよりもR も含めプログラム言語により以下のような利点を得ることができます。

① 基本的な記述方法を習得すればその応用で重回帰や階層ベイズなどいろいろなモデルを実行できます。分析手法ごとにパッケージソフトの利用法を学習する必要はありません。自前のモデルを作ることもできます。

② 分析結果に信頼を得ることが大切です。データの編集から結果に至る全ての経緯をマークダウン機能を用いることで記録し再現できます。またそのレポートを容易に作成できますから分析者の大幅な負担軽減が図れます。

③ 特定の確率モデルから乱数を発生させデータを作る、サンプル数による精度の違いを試すなど手で触るような学習が可能です。思いついたことを試してみる感覚があれば理解は早く進むと思います

<文/山田 聖二郎>

※本記事の個別授業としてこちらがおすすめです！

Stanによるベイズ統計学習