こんにちは。和からの数学講師の岡本です。以前マスログで「白銀比」という比率をご紹介しました。実は白銀比には2種類あり、今回はもう一つの白銀比を紹介します。

１．以前紹介した白銀比

以下のマスログで、黄金比と白銀比についてまとめました。詳しい内容はこちらをご覧ください。

デザインとアートの不思議な比率～黄金比と白銀比～

デザインやアートの世界で話題になる「黄金比」のほかに「白銀比」と呼ばれる比が存在し、割と身近な場面で現れます。

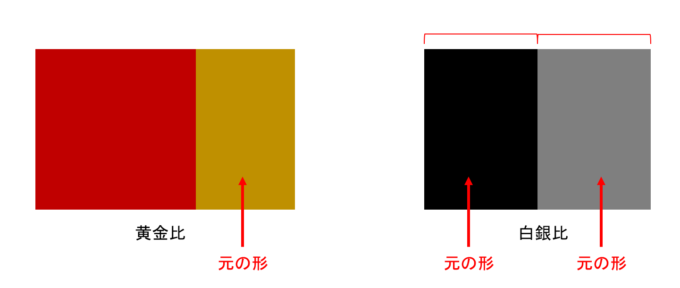
白銀比は「\(1:\sqrt{2}\)」という比率で、この比の長方形の長い辺を半分にしてできる小さな長方形も、同じく白銀比になっています。こうした性質から、A判サイズなどの用紙の規格サイズとして使われています。

２．もう一つの白銀比

実は「白銀比」はこれ以外にもう一つ存在し、その比は「\(1:1+\sqrt{2}\)」となります。同じ名前が付いているのはいささかわかりにくいので、このマスログでは、この比の事を「第1種白銀比」と呼び、\(1:\sqrt{2}\)の方を「第2種白銀比」と呼ぶことにします。なんだか意外だと思いませんか？どうして\(1\sqrt{2}\)の方が「第2種」なのかでしょう？その理由は簡単です。実は\(1:1+\sqrt{2}\)の比の方が正当な黄金比の一族と言えるのです！

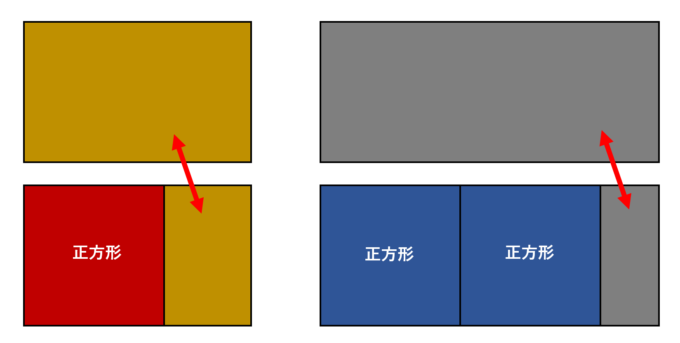
では、前回と同様に第1種白銀比の長方形を考えてみます。第2種と比べてやや横長です。ここでは「第1種白銀長方形」と呼ぶことにします。黄金長方形の性質は「短い辺を一辺とする正方形を1つ取り除いてできる小さい長方形も最初と同じ比の長方形になる」というものでした。実は、第1種白銀長方形の場合、「短い辺を一辺とする正方形を2つ取り除いてできる小さい長方形も最初と同じ比の長方形になる」という性質を持っています。この意味で第1種白銀比は黄金比の一般化だといえるのです！

３．貴金属比と2次方程式

実は正方形を何個取り除くかによっていくらでも長方形は一般化できます。たとえば「短い辺を一辺とする正方形を\(n\)個取り除いてできる小さい長方形も最初と同じ比の長方形になる」という性質を考えてみましょう。このような性質を満たす長方形の比を「第\(n\)貴金属比」と呼びます。つまり黄金比は第1貴金属比、第1種白銀比は第2貴金属比というわけです。ちなみに第3貴金属比は「青銅比」という名前が付いていますが、残念ながら応用は見たことがないです。多分、gold, silver, bronzeまで名前を付けたかったのだと思います。また、第4貴金属比以降は一般に固有の呼び方はないようです。

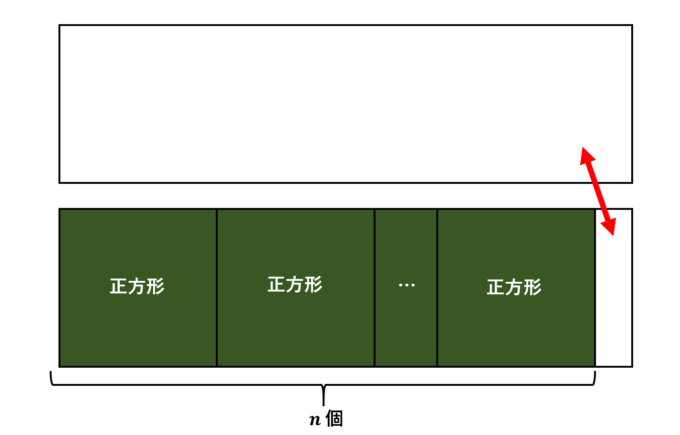
さて、それでは、第\(n\)貴金属比を実際に求めてみましょう。短い辺を\(1\)、長い辺を\(x\)としましょう。このとき、\(x\)の条件は

\begin{align*}
1:x=x-n:1　\Longrightarrow x^2-nx-1=0
\end{align*}

となり、2次法方程式の解の公式より\(x=\frac{n\pm \sqrt{n^2+4}}{2}\)であることがわかります。ただし、求める\(x\)は長方形の長さ（＝正の値）であることから、第\(n\)貴金属比は

\begin{align*}
1:\frac{n+\sqrt{n^2+4}}{2}
\end{align*}

であることがわかりました。\(n=1\)とすると確かに黄金比\(\frac{1+\sqrt{5}}{2}\)、\(n=2\)とすると第1種白銀比\(1+\sqrt{2}\)になります。

４．第1種白銀比で遊ぶ

せっかくなので第1種白銀比の性質とそれを使った遊びを紹介します。実は第1種白銀長方形のコピーを45°回転、90°回転、135°回転させると、図のように頂点が一致します。つまり、正八角形が出来上がります。

これが第1種白銀比の大きな特徴です。せっかくなので、（唐突ですが）この性質を使って東京大学の入試問題を解いてみましょう。

2003年に出題された1文だけの超印象的な問題です。この問題を解くのに、第1種白銀比の性質を使います。

【証明】方針は「円周の長さ」＞「内接する正八角形の周の長さ」を計算することで証明します。まず一辺の長さが\(1\)の正八角形を考えます。前節の話から第1種白銀長方形を考えることができ、この長方形の対角線に長さは三平方の定理より

\begin{align*}
\sqrt{1^2+(1+\sqrt{2})^2}=\sqrt{4+2\sqrt{2}}
\end{align*}

であることがわかります。

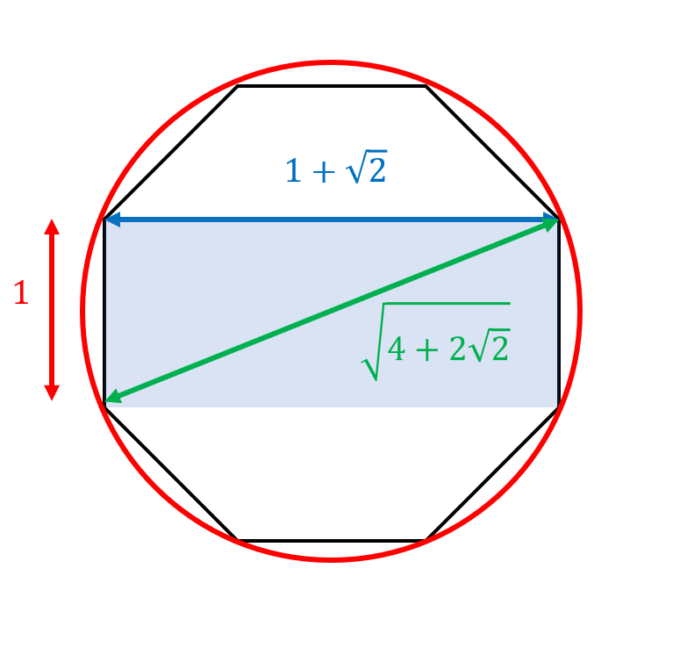
正八角形の周の長さは\(8\)であり、外接する円周の長さは\(\pi \sqrt{4+2\sqrt{2}}\)となります。これにより

\begin{align*}
\pi \sqrt{4+2\sqrt{2}}>8\Longleftrightarrow \pi>\frac{8}{\pi \sqrt{4+2\sqrt{2}}}
\end{align*}

となります。あらかじめ\(\sqrt{2}<1.415, \sqrt{6.83}<2.62\)であることを確認しておきましょう（両辺2乗すれば確かめられます）。これにより

\begin{align*}
\pi>\frac{8}{\pi \sqrt{4+2\sqrt{2}}}>\frac{8}{\sqrt{4+2\times 1.415}}=\frac{8}{\sqrt{6.83}}>\frac{8}{2.62}=3.053\cdots
\end{align*}

となり、円周率\(\pi\)が3.05よりも大きいことが証明できました。幾何学的な視点は面白いですね！

４．さいごに

いかがでしたでしょうか？今回は白銀比や貴金属比について紹介してきました。比率に関する美しさはデザインやアートの世界では欠かせない道具となっています。和からのオンラインセミナーでは、こうした数学的デザインに関する無料のセミナーもあるので、興味のある方は是非ご参加ください！

数学的デザイン超入門

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>