【難関】モーリーの定理の証明－アラン・コンヌによる代数的証明－

ロマンティック

公開日

2021年2月14日

更新日

2021年2月14日

こんにちは。和からの数学講師の岡本です。以前、モーリーの定理を紹介し、三角比を使った証明を解説しました。今回は1982年に“数学界のノーベル賞”とも言われるフィールズ賞を受賞した天才数学者アラン・コンヌによる「代数的な別証明」の概説をしていこうと思います。（※もちろんですが、モーリーの定理の別証明がフィールズ賞受賞理由ではありません。）
なお、コンヌによる証明は以下のURLから読むことができます。きちんと内容を理解したい方はこちらをご覧ください！

https://www.alainconnes.org/docs/morley.pdf

この記事の主な内容

１．モーリーの定理（再掲）

ひとまず、モーリーの定理の主張を述べます（詳しくは過去のマスログをご覧ください)

モーリーの奇跡

定理（フランク・モーリー,1899）
任意の三角形の各頂点から、角の3等分線を伸ばす。
２つの頂点の隣り合う3等分線の交点を結ぶと正三角形ができる。

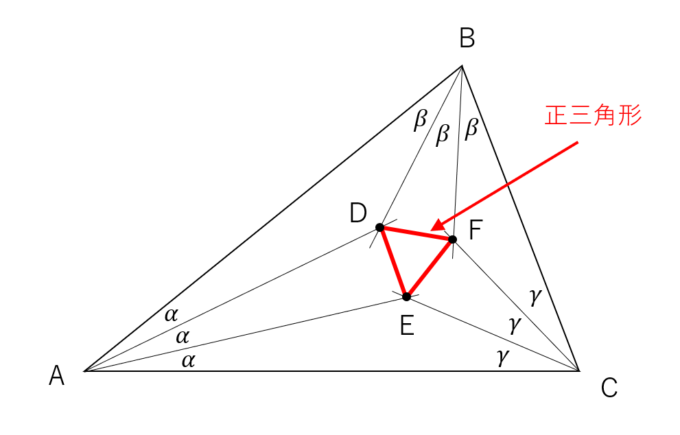
いやー！何度見ても美しいですね！！
このシンプルな結論の美しさにコンヌも魅了され、証明を一生懸命考えたのでしょう。

２．不動点という視点

例のように各頂点から3等分線を引きます。こうしてできた「交点」をコンヌは「ある変換の不動点」と考えました。なかなか思いつかない発想ですよね…！
ここでいう変換というのは「回転」や「平行移動」、またそれらの組み合わせを意味します（「運動」と表現するとわかり易いかもしれません）。
実際に、点Aを中心に\(2\alpha\)回転させる変換を\(g_A\)、点Bを中心に\(2\beta\)回転させる変換を\(g_B\)、点Cを中心に\(2\gamma\)回転させる変換を\(g_C\)としましょう。三角形ABCに関して\(g_A\)の変換を行うと、もちろんですが回転の中心Aだけ動きません。このような、変換しても動かない点を不動点と呼び、変換\(S\)の不動点を\(\text{Fix}(S)\)と書くことにします。では、変換\(g_A\)の後に変換\(g_B\)を続けて行う合成変換\(g_Ag_B\)を考えましょう。

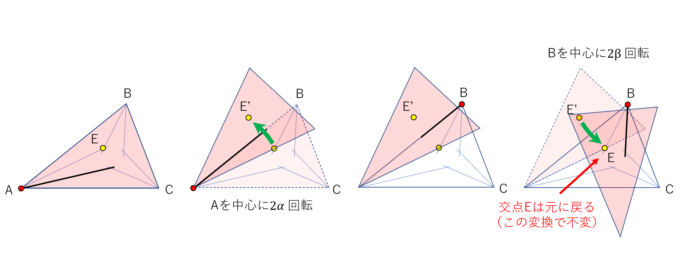
この変換で動かない点が実は上図の交点Eなのです。つまり、

\begin{align*}
\text{Fix}(g_Ag_B)=E
\end{align*}

となります。もうひとつ面白い変換を考えてみましょう。それは、変換\(g_A\)を3回行い、変換\(g_B\)を3回を行い、さらに変換\(g_C\)を3回行うという合成変換\(g_A^3g_B^3g_C^3\)を考えます。実際に三角形全体を動かしてみたのが下図です。

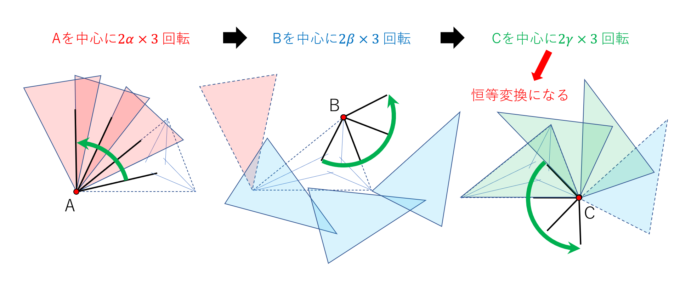
なんということでしょう！三角形は元に位置に戻ってきました！つまり、合成変換\(g_A^3g_B^3g_C^3\)は変換を行わない「恒等変換」だったということがわかりました。このような図形や空間を「変換する」という操作全体の集合は数学における「群」という構造を持ちます。コンヌはこの群という概念を使った「代数的手法」でモーリーの定理の証明を試みたのです。

３．コンヌの定理とモーリーの定理

まず、モーリーの定理の証明のために、コンヌが示した一般的な形の定理を紹介します。そのためにいくつか準備をしておきましょう。

体という四則演算が大体不自由なくできる集合\(k\)を考え、その上のアフィン群\(G\)を考えます。言い換えると、\(x\in k\)に対して、\(a\in k^{\times}=k\setminus\{0\}\)と\(b\in k\)を用いて

\begin{align*}
x\mapsto ax+b
\end{align*}

という変換全体の集合が\(G\)となります。ざっくりいうと、「\(a\)倍」というのは「回転と拡大・縮小」を表し、「\(+b\)」というのは「平行移動」を表します。そこで、上のような変換を\(g\in G\)とし、この変換の「回転と拡大・縮小」の情報だけを取り出す対応\(\delta:G\longrightarrow k^{\times}\)を考えます。つまり\(\delta(g)=a\)と定義します。この対応\(\delta\)により、\(1\in k^{\times}\)に送られるような\(G\)の元の集合を\(T\)とします（つまり、\(T=\mathrm{Ker}(\delta)\)）。\(T\)は平行移動のみの変換となることがわかります。これでコンヌの定理を述べる準備ができました。

定理（アラン・コンヌ）
体\(k\)上のアフィン群\(G\)の元\(g_1, g_2, g_3\)を考える。ただし、\(g_1g_2, g_2g_3, g_3g_1, g_1g_2g_3\)はどれも平行移動でないとする。また、\(j:=\delta(g_1g_2g_3), \alpha :=\text{Fix}(g_1g_2),\beta :=\text{Fix}(g_2g_3),\gamma :=\text{Fix}(g_3g_1)\)と表す。このとき次の(1)と(2)は同値となる。

(1)\(g_1^3g_2^3g_3^3=1\)（ただし、\(1\)は恒等変換を意味する）

(2)\(j^3=1\)であり、\(\alpha +j\beta+j^2\gamma=0\)

もともとのモーリーの定理からかなりかけ離れた内容になってきました。そもそも何をいってるのかわからなくなってきそうですね（笑）。

コンヌの定理の証明は論文（https://www.alainconnes.org/docs/morley.pdf）あるいはかの有名なブログINTEGERS（http://integers.hatenablog.com/entry/2017/08/30/022712）にて解説があるので興味のある方はご覧ください。

さて、コンヌの定理における体\(k\)を複素数の集合\(\mathbb{C}\)で考えます。すると面白いことに、最初に考察した変換\(g_A,g_B, g_C\)が全てアフィン群の元で、コンヌの定理の\(g_1, g_2, g_3\)として具体的に計算することができます。つまり、点A～Fまでを複素平面上の点と考えるとことで、\(\text{Fix}(g_Ag_B)=E, \text{Fix}(g_Bg_C)=F, \text{Fix}(g_Cg_A)=D\)であり、さらには（１）の条件\(g_A^3g_B^3g_C^3=1\)が成り立っています。つまり、\(j^3=1\)なる複素数\(j\)を使って、以下が成り立ちます。

\begin{align*}
E+jF+j^2D=0
\end{align*}

3乗根\(j\)を使ったこの等式は、E,F,Dの配置が正三角形であることを意味します。つまり、自動的にモーリーの定理が証明できたのです！！