デザインとアートの不思議な比率~黄金比と白銀比~
公開日
2020年12月13日
更新日
2020年12月13日
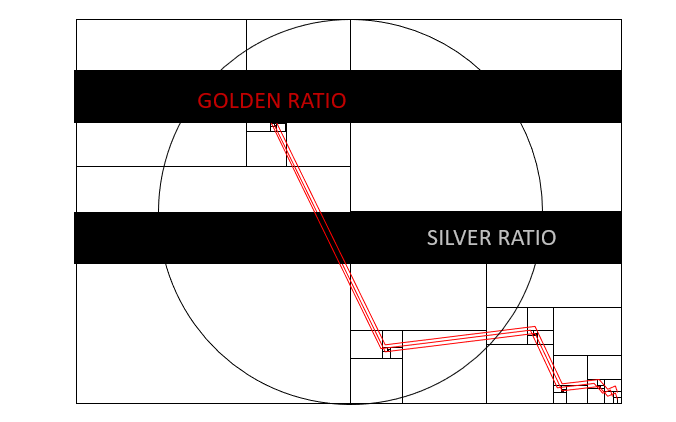
こんにちは。和からの数学講師の岡本です。みなさんは「黄金比」ってご存じですか?アートや自然界のいたるところで現れる、不思議な比率で、実際に多くのロゴやデザインなんかにも使われています。この他にも、白銀比と言われる比率が存在します。今回は、様々な比率とその魅力について簡単にまとめていこうと思います。
この記事の主な内容
1.黄金比とは?
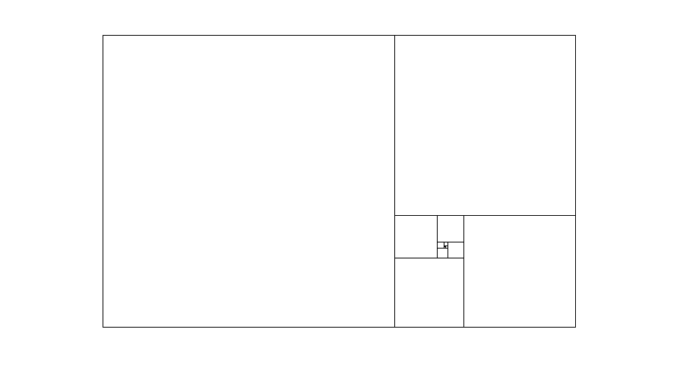
よく耳にする「黄金比」。それは以下のような長方形の縦と横の比のことを言います。

短い辺の長さを一辺とする正方形を長方形の内側に考えます。すると残りの部分に小さな長方形ができあがります。この小さな長方形と、元の大きな長方形の「形が同じ」である長方形を「黄金長方形」と呼びます。この長方形の縦と横の比を「黄金比」と呼び、それはおおよそ1:1.618 という比率になっています。黄金比はこれ以外にも多くの不思議な性質を持ち、レオナルド・ダ・ヴィンチの時代には「神聖比(Divine Proportion)」と呼ばれていました。
2.コピー用紙の比率
黄金比は多くの建築や、デザイン、芸術作品の中で使われているといわれます。しかし、実際に私たちが目にする身近な長方形の比率はほとんど黄金比でしょうか?例えば、名刺や印刷用紙などを測ってみると、比は1.618よりも明らかに小さい値になっています。A4サイズというのは210[mm] \(\times\) 297[mm]です。この比を計算すると
\begin{align*}
\frac{297}{210}=1.4142\cdots
\end{align*}
となります。やはり、1.618よりも小さいですね。では、A3サイズの297[mm]\(\times\) 420[mm]の比を計算してみましょう。
\begin{align*}
\frac{420}{297}=1.4141\cdots
\end{align*}
おや?A4サイズの比とほぼ同じですね!実は、全てのA判の用紙は、約1:1.414の比になっています!ちなみに1.414というのは\(\sqrt{2}\)の値です。
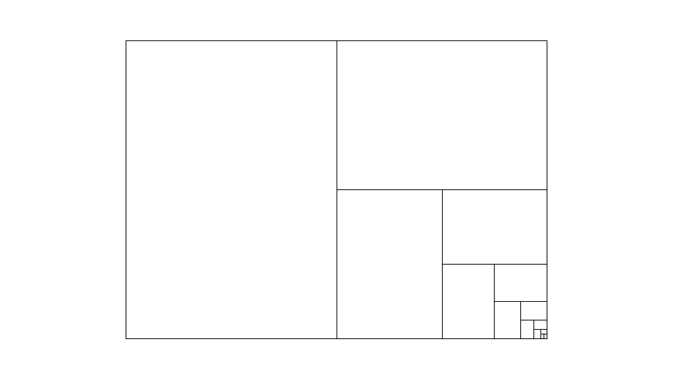
この比率は19世紀の化学者ヴィルヘルム・オストヴァルト(1853~1932)によって考案されたもので、\(1:\sqrt{2}\)の比で統一されています。この比率は「白銀比」と呼ばれ、黄金比とは違った特性があります。それは
「長い辺で半分に折っても(切っても)同じ形の長方形になる」
という特性です。長い辺を半分にすると
\begin{align*}
1:\frac{\sqrt{2}}{2}=1:\frac{1}{\sqrt{2}}=\sqrt{2}:1
\end{align*}
となり、短い辺と長い辺の比は\(1:\sqrt{2}\)になります。
3.問題
こんな問題を考えましょう。
短い辺の長さを\(x\)[m]としましょう。このとき長い辺の長さは\(\sqrt{2}x\)[m]と表現できます。いま、面積が1[㎡]ということなので、
\begin{align*}
x\times \sqrt{2}x=\sqrt{2}x^2=1\Longrightarrow x=\sqrt{\frac{1}{\sqrt{2}}}=0.84089\cdots
\end{align*}
となり、短い辺の長さは約0.841[m]=841[mm]、そして、\(\sqrt{2}\)倍することで長い辺の長さは約1189[mm]となります。実はこれが「A0サイズ」となります。このサイズを半分にしたものが「A1サイズ」。同様にA2, A3, A4と小さくなっていきます。実際に計算してみると納得ができますね!
4.さいごに
いかがでしたでしょうか?今回は身近な「比率」に注目し、実際にコピー用紙の長さを計算してみました。比率や幾何学といった数学は私たちの日常の中に豊富に存在しています。この機会にいろいろなものの比率についれ実際に計算してみてはいかがでしょうか?
なお、「黄金比」に関するデザインや数学は、和からのオンラインセミナーで学ぶことができます!いままでと全く違った数学の学び方をご提供いたします!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>













