美しきタイリングの世界～数学を使った模様の捉え方～

公開日

2021年1月21日

更新日

2021年1月21日

こんにちは。和からの数学講師の岡本です。前回に引き続き、タイリング模様についてのお話です。今回は数学を使ったお話を混ぜていきます。

この記事の主な内容

１．平面タイル貼り

平面にタイルを綺麗に敷き詰める方法が無限にあります。例えば以下のように様々な種類のタイルを使えば可能ですし、むしろ平面を適当に砕くことでタイルができます。

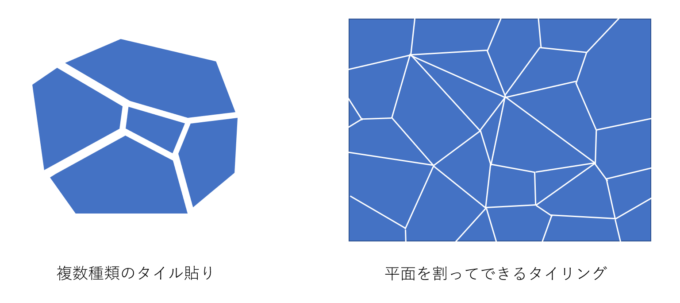
しかし、タイルの種類や形が限られている場合はどうでしょう？話がずいぶん変わってきますね。例えば「１種類の正多角形タイル」ではどうでしょうか？前回に少しだけ言及しましたが、実は、本質的に3通りしかないことが知られています。

２．正三角形と正方形と正六角形

1種類の正多角形におけるタイリングは本質的には以下の3種類しかないことが証明されています。

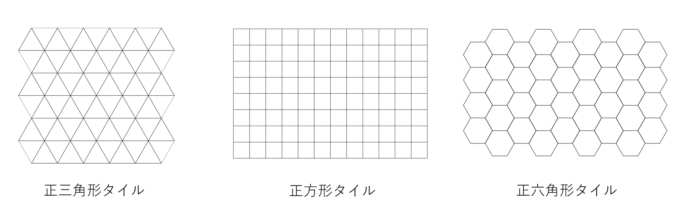
「本質的に」という言葉がどうも気になりますよね。これは、上のタイリングを「ずらす」ことによって、多様なタイリングに変形できることを考慮しています。

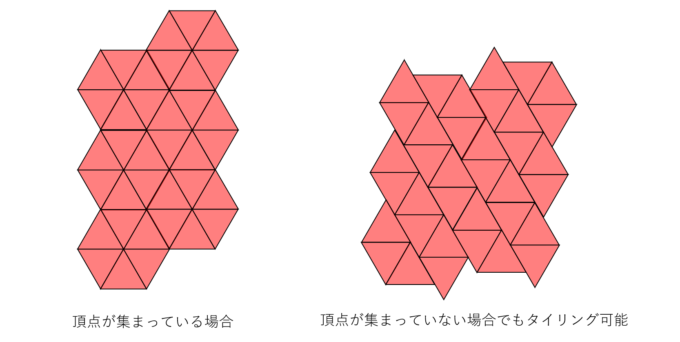
上の図のように、タイルをずらしてもタイリングできています。このような変形を含めず、頂点がしっかり合わさるようなタイリングを考えるとそれが3種類となるのです。
では、実際に証明してみましょう。

３．3種類しかないことの証明

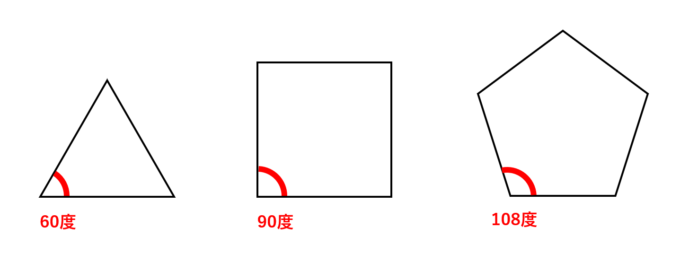
まず、正多角形の内角について説明しましょう。例えば、正三角形の内角はみなさんご存じの通り\(60\)度です。正方形は\(90\)度、そして正五角形は\(108\)度となります。内角の総和を考えると、正三角形の場合\(60\times 3=180\)度、正方形の場合\(90\times 4=360\)度、正五角形の場合\(108\times 5=540\)度となります。

だんだんと内角の総和が大きくなりますね。しかも角が１つ増えるごとに\(180\)度大きくなっています。実際に正\(n\)角形の内角の総和は\((n-2)\times 180\)度となります。つまり、1つの内角はこの角度を\(n\)で割ることで得られ、\((1-2/n)\times 180\)度となります。さて、正\(n\)角形1種類でタイリングができたとします。タイリングができているということは頂点周りに正多角形がちょうど1周できるということです。例えば、正\(n\)角形を\(m\)個用いることで、1周（\(=360\)度）が実現できたとします。これは数式で表すと

\begin{align*}
\left(1-\frac{2}{n}\right)\times180\times m=360 \Longrightarrow \frac{1}{n}+\frac{1}{m}=\frac{1}{2}
\end{align*}

を意味します。実は、上の等式を満たす正の整数\(n, m\)は簡単な計算から\((n,m)=(3,6),(4,4), (6,3)\)しかないことがわかります。これはそれぞれ「正三角形6個」「正方形4個」「正6角形3個」を意味し、これ以外の正多角形はタイリングできないことがわかります。なお、それぞれのタイリングは最初にお見せした3種類のタイリングとなるわけです。

４．さいごに

いかがでしたでしょうか？今回はタイリングの可能性について、少し数式を使って紹介してみました。タイリングの世界は非常に奥が深く、まだまだ面白い事実や性質があります。またトピックがあれば、マスログで紹介していこうと思います。
和からでは、こうした「数学的なデザイン」の捉え方や考え方に関するセミナーを開催しております。興味のある方は是非ご参加ください！