こんにちは。和からの数学講師の岡本です。前回に引き続き、フラクタル図形のテーマでお話ししていきます。前回の内容のマスログはこちら。
今回は自己相似性と次元についてのお話です。

フラクタルってなに？～その特徴と歴史その①～

１．自己相似性

自己相似性をもつ図形とは、簡単にいうと、その図形の縮小された形で構成されている性質のことを言います。例えば、図のような「シェルピンスキー・ギャスケット」と呼ばれる三角形は元の1/2の図形３個分でできています。

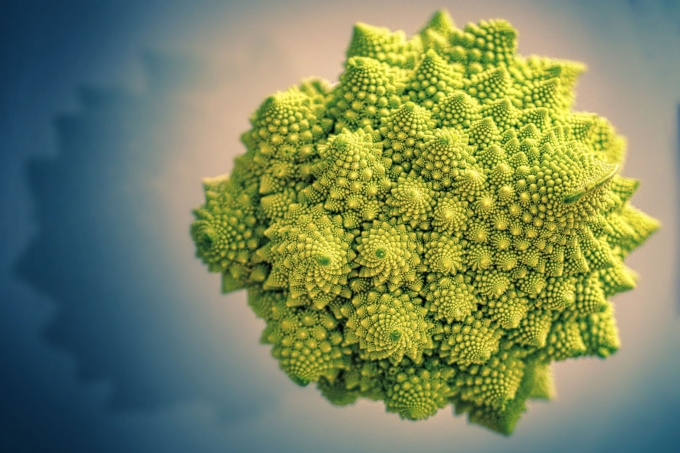
自然界の中にもフラクタル図形はあちらこちらに存在しており、わかり易い例として「ロマネスコ」という野菜があります。写真からわかるように、同じ形の繰り返しにより全体が構成されています。このような「非現実感」がフラクタル図形やフラクタル・アートの魅力に１つになります。

２．フラクタルの次元

みなさんは何次元の世界に住んでいますか？縦、横、高さという３つの軸で位置が決まるので「３次元」とも考えられますし、時間の経過も含めると実は４次元とも取れます。このように次元とは「軸の個数」とするのが「位相次元」という考え方です。
実は次元の概念にもさまざまな一般化があり、ボックス次元、相似次元、など数多く存在します（基本的にどの次元も結果として同値になることが知られているので、これらの次元をまとめて「フラクタル次元」と呼びます）。今回ご紹介するのはその中の「相似次元」です。
相似次元とは、元の図形Aのが、\(1/N\)スケールの図形\(n\)個分で構成されるとき、Aの相似次元\(D\)は

\begin{align*}
n\left(\frac{1}{N}\right)^D=1
\end{align*}

を満たすものとして定められます。例えば、長方形を考えます。

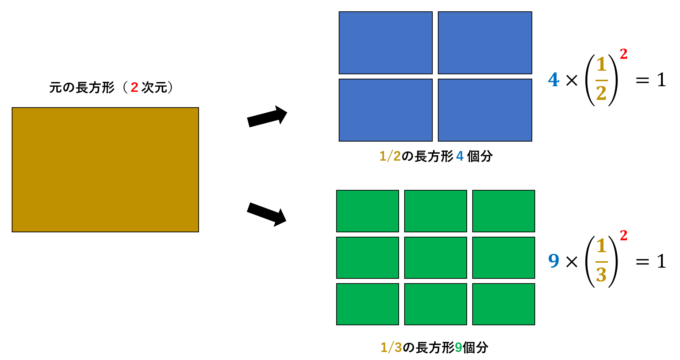
これらの\(1/2\)スケールの長方形を\(4\)個使うことで、元の長方形を再現できます。同様に\(1/3\)スケールの長方形を\(9\)個使うことで再現できます。いずれの場合も

\begin{align*}
4\left(\frac{1}{2}\right)^D=1,\hspace{1.0em}9\left(\frac{1}{3}\right)^D=1
\end{align*}

を満たす\(D\)として\(D=2\)があてはまります。これにより長方形は\(2\)次元であると考えられるのです！

３．シェルピンスキー・ギャスケットの次元

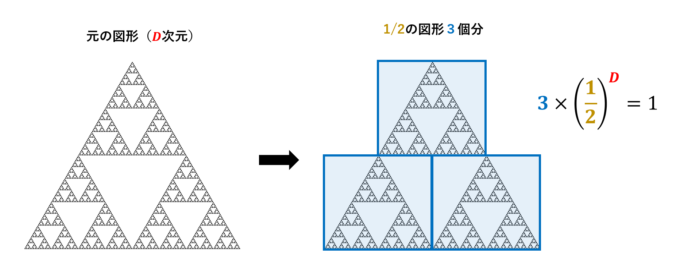
では、シェルピンスキー・ギャスケットの相似次元を計算しましょう。図のように、\(1/2\)スケールのギャスケット\(3\)個分で再現できるので、相似次元\(D\)は

\begin{align*}
3\left(\frac{1}{2}\right)^2=1
\end{align*}

どうやら整数値ではなさそうです。実際にこの式を満たす\(D\)を計算するには対数関数を使う必要があり、結果として

\begin{align*}
D=\frac{\log 3}{\log2}=1.584962\cdots
\end{align*}

となります。なんと１次元の２次元の間の図形だったのです！ちなみにこの図形、面積０で、境界線の長さは無限大！なんとも不思議ですね！このことから、いままでの図形の捉え方の範疇を超えているのが実感できますね。

４．さいごに

いかがでしたでしょうか？今回はフラクタルの創始者マンデルブローの考えた、フラクタルの２つの特徴その１「自己相似性」についてお話してきました。次回はもう一つの特徴である「ギザギザ性」について簡単に解説していきます。お楽しみに！

和からではフラクタルに関するアートセミナーを実施しています。
興味のある方はまず、無料のセミナーへお越しください！

Excelアート超入門

Excelで学ぶアート数学-フラクタルとカオス編-

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>