偏角の原理を使って五次方程式を解く
公開日
2020年12月23日
更新日
2020年12月23日
この記事は、日曜数学 Advent Calendar 2020 – Adventar(外部サイト)23日目の記事です。22日目はヘカテーさんの「論理パズルの解説と、ハミング符号。」でした。
和からの松中です。今回は五次方程式と偏角の原理について語らせていただきます。
この記事の主な内容
五次方程式は解けない?
私たちは中学校の時に二次方程式の解の公式を学びました。
\(ax^2+bx+c=0\)の解は、\(\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\)
紀元前2000年頃のエジプトで具体的な問題に対して二次方程式が解かれていたようです。また、紀元前300年頃のユークリッドの原論には幾何的な方法による二次方程式の解法が載っており、7世紀のアラビアでは現在の解の公式が発見されていました(そもそも当時は負の概念すらないので、表記法は現在とは異なるはずですが)。
二次方程式が解けるようになったら、三次方程式や四次方程式も解きたくなります。そして実際に、16世紀のイタリアで三次方程式、四次方程式についても解の公式が発見されました。しかし現在の私たちは三次方程式と四次方程式の解の公式を中学、高校で学びません。これはおそらく二次方程式に比べて三次方程式、四次方程式を使わないと解けない問題が身の回りに少ないことと、その解の公式があまりにも複雑で、純真でいたいけな中高生に教えることのはやめたほうがよい、という教育的な配慮によるものと思います。
とにもかくにも、16世紀に立て続けに四次方程式の解の公式まで発見されたため、人々の期待は五次方程式の解の公式の発見に向くのですが、その後300年以上、五次方程式の解の公式が発見されることはありませんでした。それどころか、19世紀にアーベルやガロアによって独立に「五次方程式には解の公式が存在しない」ことが証明されてしまうのです。
ここで注意したいことは五次方程式に解の公式は存在しなくても、五次方程式の解は存在するということです。解の公式とは「方程式の係数に対して四則演算や\(n\)乗根を取る操作を有限回繰り返して解を書き下したもの」です。確かに二次方程式の解の公式も係数である\(a\)、\(b\)、\(c\)に四則演算とルートをとる操作を何回か行って解を書き下していますね。
アーベル、ガロアが証明したことは、「五次方程式には解が存在しない」ということではなく、「五次方程式の解は、その係数の四則演算や\(n\)乗根を取る操作を有限回繰り返して書き下すことができるとは限らない」ということだったのです。
「五次方程式には解の公式はない!!」が、「五次方程式に解は存在する!!」と言われると、とてももやもやします。結局解けるの?解けないの?という気分になります。今回は五次方程式を数値的に解く方法を思いつきましたので、紹介させていただきます。
偏角の原理
本記事で五次方程式を解くために用いる道具は複素関数論の「偏角の原理」です。
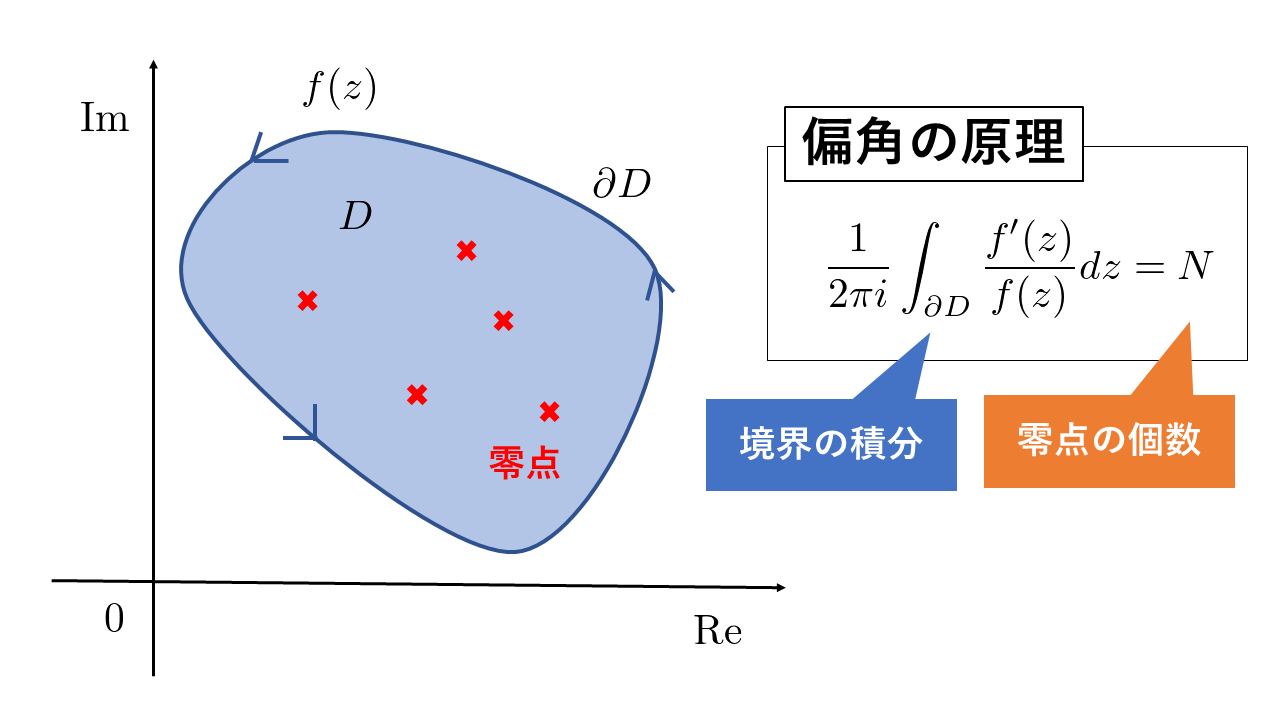
\(C\)をなめらかな単一閉曲線とし、\(f(z)\)は\(C\)上及び、\(C\)の内部で正則とする。
また、\(C\)の内部にある\(f(z)\)の全ての零点の個数を重複度も込めてカウントしものを\(N\)とする。
このとき(なんと!!)
\[
\frac{1}{2\pi i}\int_C\frac{f^{\prime}(z)}{f(z)}dz=N
\]
が成り立つ。
(注:偏角の原理はより一般に\(C\)内に極があるような\(f(z)\)に対しても同じような主張をしているのですが、本記事では極がある関数は扱わないため上のように紹介しています。ある意味上の主張は偏角の原理一歩手前(偏角の定理\(\beta\)版)です。
つまり一言でいうと、「複素平面上の領域\(D\)の中に存在する\(f(z)\)の零点の個数は、\(D\)の境界に沿って\(\displaystyle \frac{f^{\prime}(z)}{f(z)}\)を積分すればわかる」ということです。個人的にはとても不思議で、驚きです。
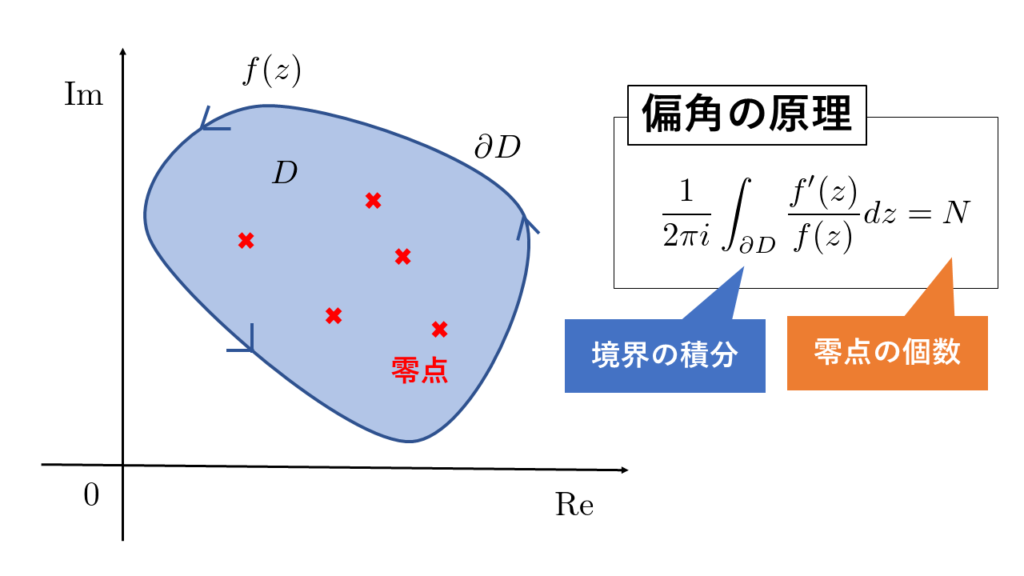
抽象的に定理の紹介をするだけではなんのことかわかりにくいので、偏角の原理を使って\(f(z)=z^2-3z+2\)の与えられた領域内での零点の個数を調べてみましょう。
\(f(z)=(z-2)(z-1)\)ですから\(f(z)\)の零点は\(z=1\)、\(2\)となります。よって以下の\(C_1\)、\(C_2\)、\(C_3\)、\(C_4\)上で\(\displaystyle \frac{f^{\prime}(z)}{f(z)}=\frac{2z-3}{z^2-3z+2}\)を積分してみると、
\[
\frac{1}{2\pi i}\int_{C_1} \frac{2z-3}{z^2-3z+2}dz = 0\\
\frac{1}{2\pi i}\int_{C_2} \frac{2z-3}{z^2-3z+2}dz = 1\\
\frac{1}{2\pi i}\int_{C_3} \frac{2z-3}{z^2-3z+2}dz = 1\\
\frac{1}{2\pi i}\int_{C_4} \frac{2z-3}{z^2-3z+2}dz = 2
\]
となることを偏角の原理は主張しているのです。実際にpythonでこのようなプログラムを作って確認すると確かに成り立っていることが分かります。
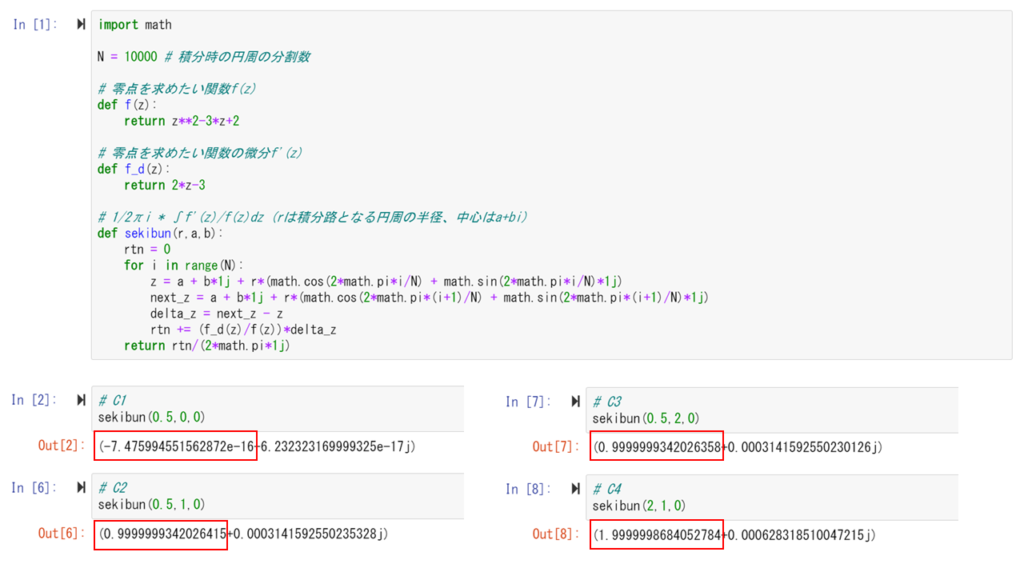
とてもおもしろいです。
積分を数値計算すると誤差が入ってしまうため、積分の結果が(理論的には)\(0\)以上の整数になるというのも個人的に嬉しいポイントです。例えば積分の結果が\(4.85+0.002i\)と出てきたら、この結果は\(5\)だなと判断してよいからです。
魚群探知機を用いるように五次方程式の解を探す
では偏角の原理を用いてどのように五次方程式を数値的に解くのかをご紹介します。
ここではわかりやすいように「魚群探知機」を例に出して紹介していくことにします。ドラゴンボールの「ドラゴンレーダー」、鬼滅の刃の伊之助の「獣の呼吸 漆の型 空間識覚」を思い浮かべてもよいかもしれません。
まず漁船を複素平面上の原点に停泊させ、魚群探知機を使って周りに魚(零点)がいるかを調べます。魚群探知機の観測距離を9kmのように大きくしておけば、少なくとも魚(零点)が1匹は入っていることでしょう。(これは元々の方程式の話では、偏角の原理を用いて原点を中心とする大きな円周上で\(\displaystyle \frac{f^{\prime}(z)}{f(z)}\)を積分し、円周内の\(f(z)\)の零点の個数を調べるということに対応しています。)
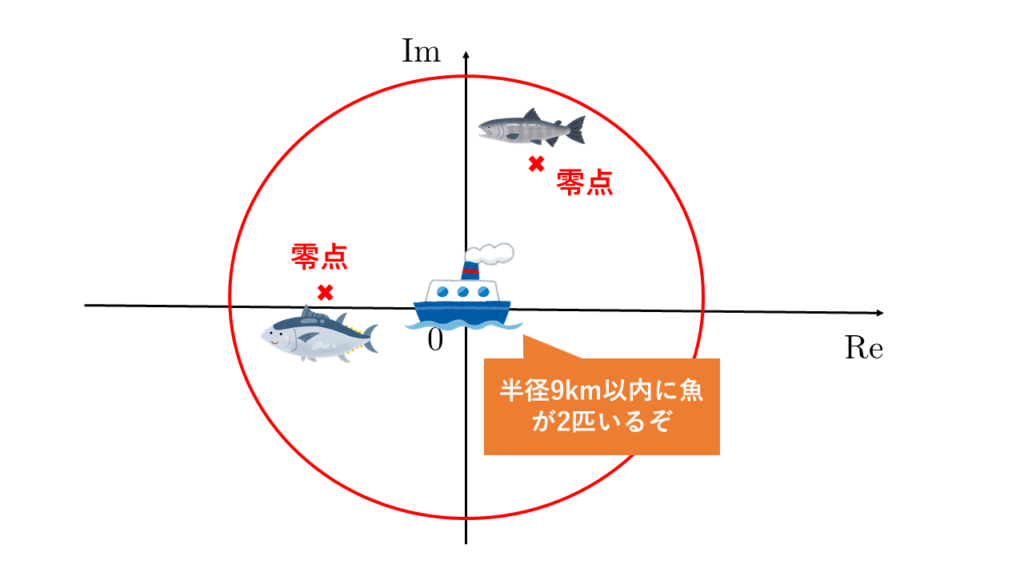
原点から半径9km以内に魚(零点)がいることがわかれば、今度は魚群探知機の観測距離を6km(さっきの2/3倍)にして、以下の8つのポイントを順に巡りながら、魚群探知機で魚(零点)を探します。
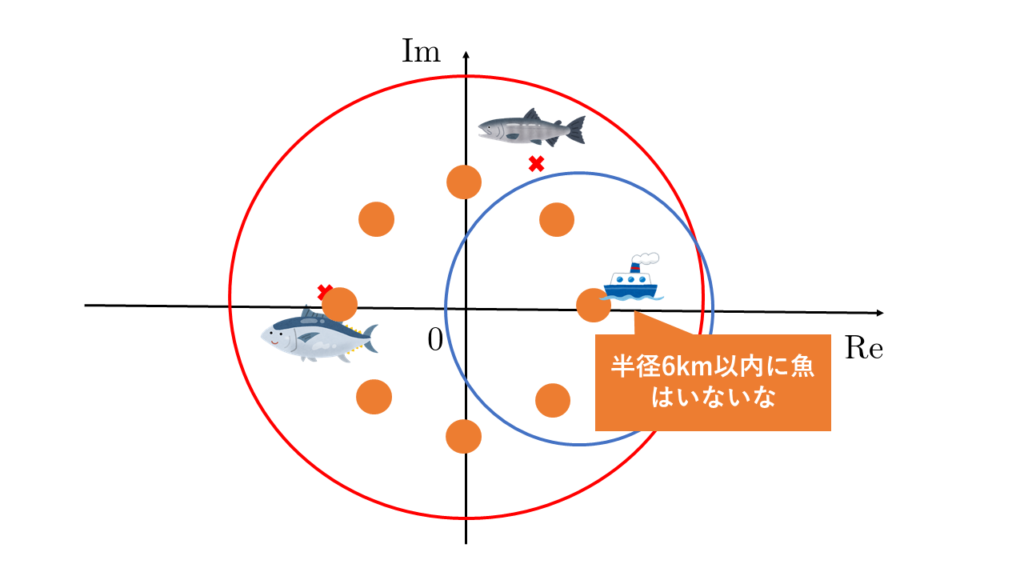
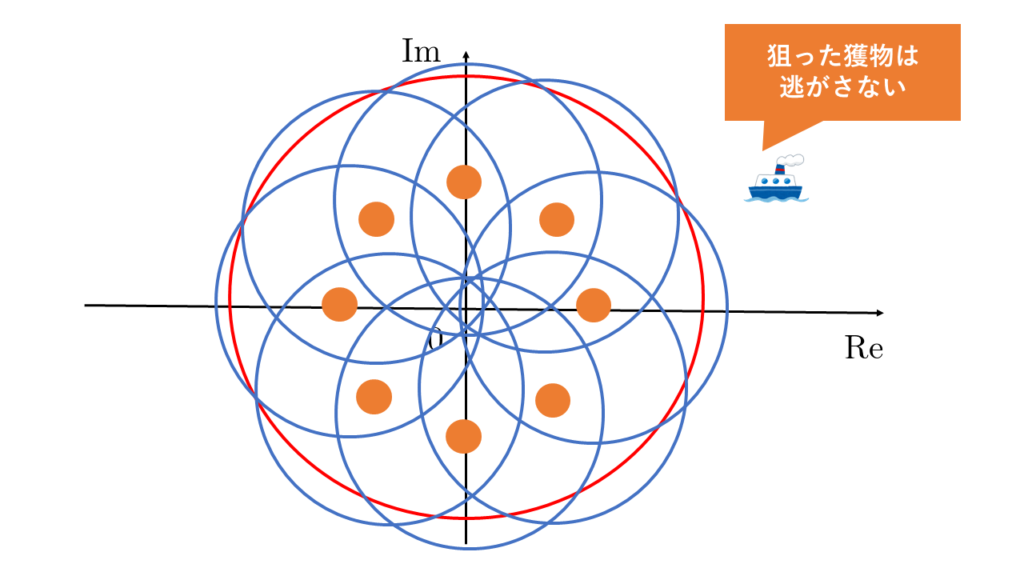
下の図を見たらわかる通り、8つの小さな円(半径6kmの円)は元々観測した大きな円(半径9kmの円)を覆っていますので、少なくとも一つのポイントで魚(零点)が発見されるはずです。
この例では2番目のポイントで魚群探知機が反応することから、海の中を見ることができない漁師でも図の青線内に魚(零点)が存在することがわかります。先ほどの赤線の円より魚(零点)が存在している領域の面積が小さくなっている点が注目ポイントです。
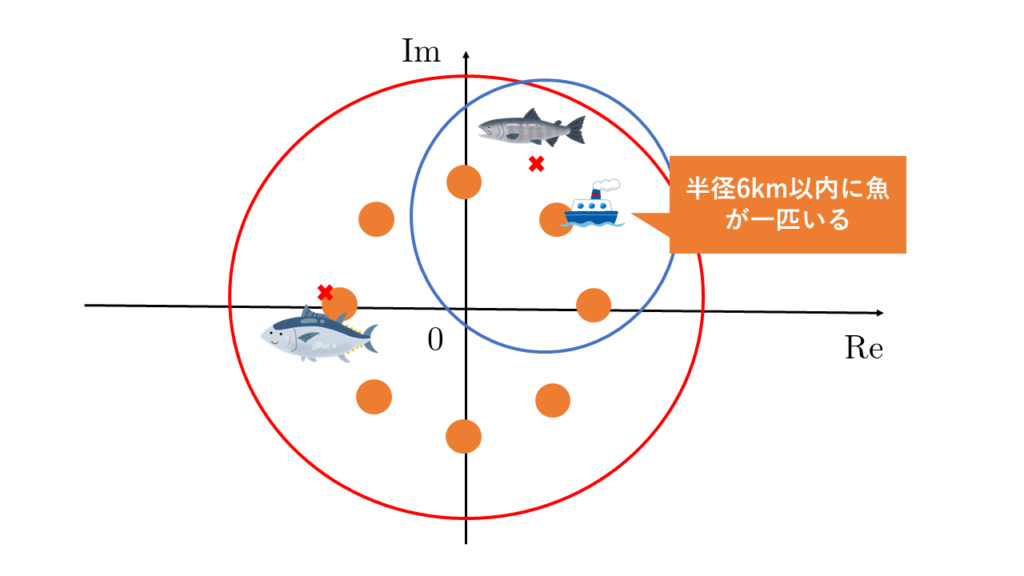
魚(零点)が見つかった半径6kmの円に対して、魚群探知機の観測距離を4km(さっきの2/3倍)にして、同じことを繰り返していきます。
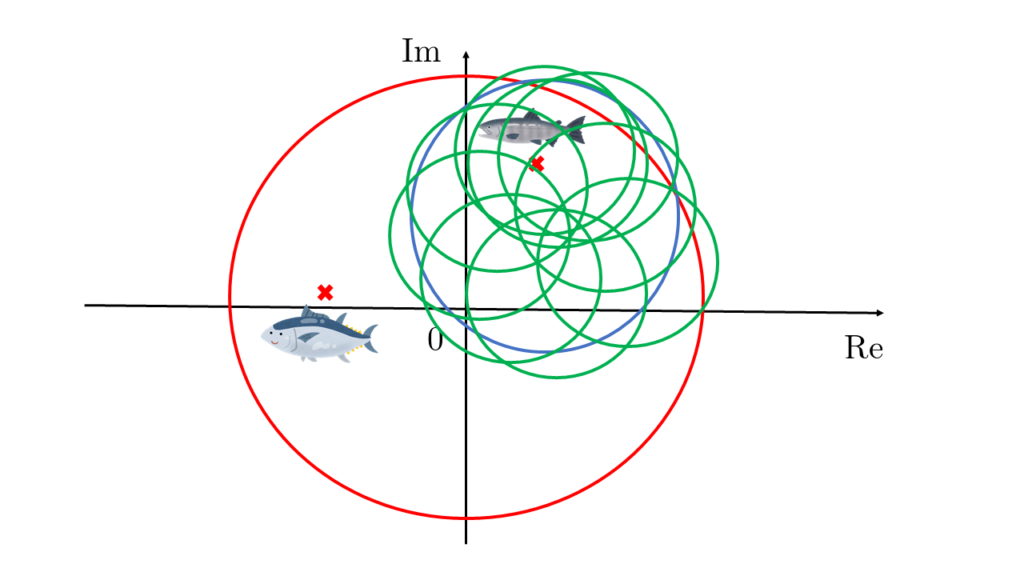
魚群探知機の観測距離は2/3倍になっていくので、これを繰り返せば確実に魚(零点)に迫っていけるのです。
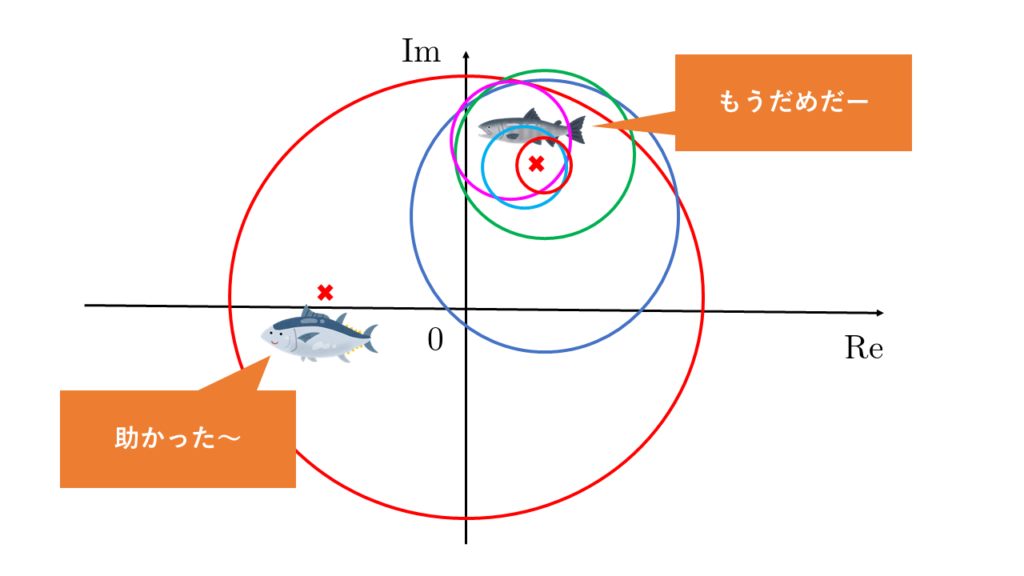
ちなみにですが、この手法は魚(零点)が複数匹いたとしてもまずは最初に見つかった一匹を確実に釣り上げるということにしています。一匹見つかればその一匹を除いた後、新しく原点に船を停泊させて同じことを繰り返せばやがてすべての魚(零点)を見つけることができます。元の方程式の世界であれば\(z=\alpha\)が\(f(z)\)の零点であることが分かったら、\(f(z)=(z-\alpha)g(z)\)を満たす多項式\(g(z)\)に対して同じ方法で零点を探していけばよいです。もちろん\(g(z)\)を用いずに元の\(f(z)\)の形のまま他の零点を探していっても問題ありません。いずれにしても二個目以降の零点を探すのは多項式の割り算をするとか、既に見つかった零点を無視するようなif文を書くとか少し面倒で本質的でもないので、本記事では扱いません。一個零点が見つかれば満足です。
実際にやってみる
詳しくは解説できませんが、上で紹介した方法をPythonで実装するとこのようなものになります。
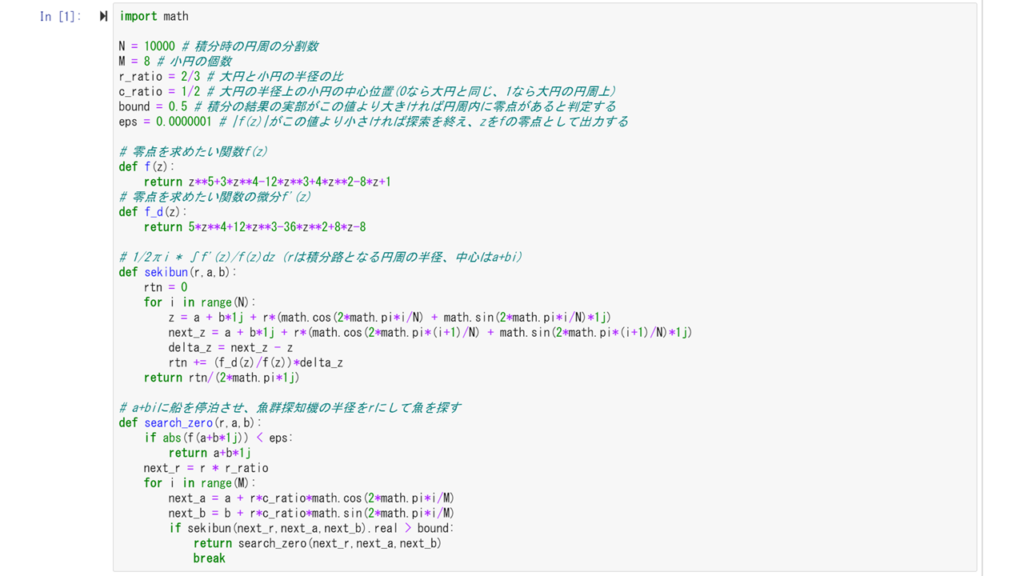
漁船の例では何度も船を動かし魚群探知を行うことからプログラムが長くなりそうと感じた方がいるかもしれませんが、大きな円で魚群探知を行うという処理の中で8つの小さな円での魚群探知を行うという処理を再帰的に入れているので、このようにとても短いプログラムになります。なお、プログラム中の\(f(z)\)と\(f^{\prime}(z)\)は解きたい方程式ごとに変えることになります。
これを用いて実際に五次方程式を解いてみましょう。
\(z^5+3z^4-12z^3+4z^2-8z+1=0\)
\(f(z)= z^5+3z^4-12z^3+4z^2-8z+1\)、\(f^{\prime}(z)=5z^4+12z^3-36z^2+8z-8\)としてプログラムを走らせた結果は以下のようになります。
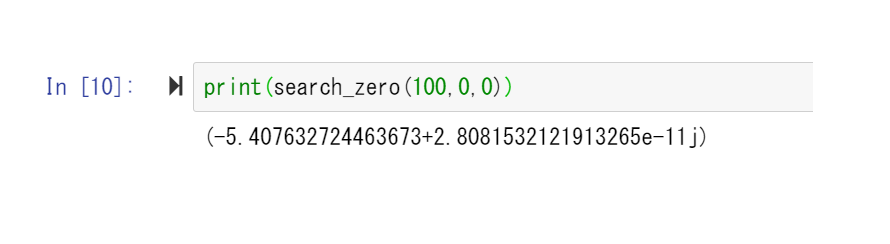
つまり、\(-5.407632724463673+2.8081532121913265\times 10^{-11}i\)が\(z^5+3z^4-12z^3+4z^2-8z+1=0\)の解の一つであることが分かりました。虚部がほぼほぼ\(0\)であるため、これは実数\(-5.407632724463673\)を表していそうです。実際に\(f(x)= x^5+3x^4-12x^3+4x^2-8x+1\)のグラフを描いてみると、
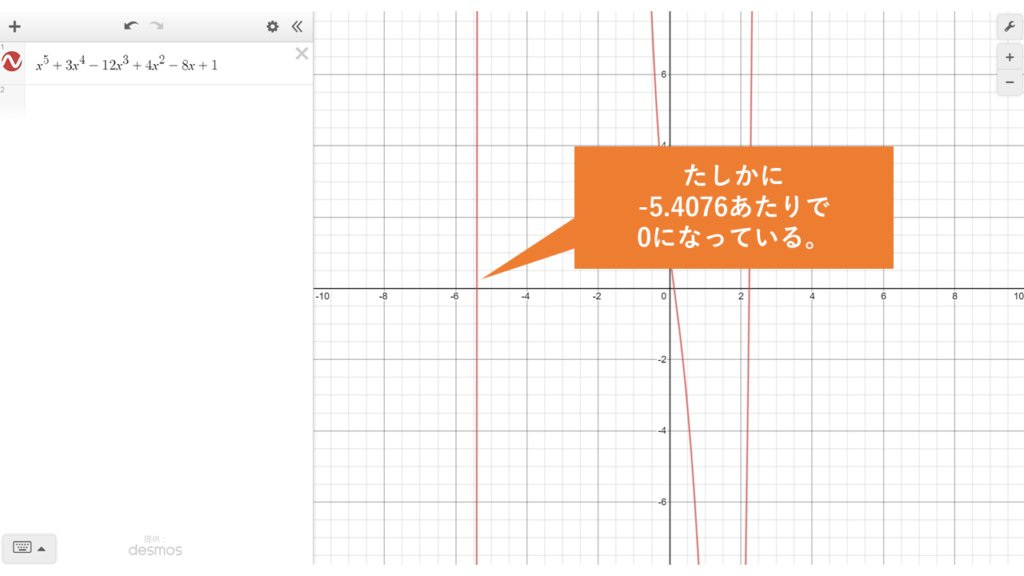
のようになり、確かに\(-5.4076\)辺りが解になっていることが分かります。
嬉しい反面、複雑な心境です。結局グラフを描けば解のおおよその位置がわかるからです。別に今回の手法を使う必要はないわけです。
グラフを考えればわかりますが、実数係数の五次方程式は少なくとも一つの実数解を持ちます。そこで今度は、係数に虚数を入れてみましょう。これで実数の関数としてのグラフを描くことができないのでこれで解を求めることができると嬉しくなります。
\(z^5+(3i+4)z^4-2iz^3+4z^2-8z+1-i=0\)
\(f(z)= z^5+(3i+4)z^4-2iz^3+4z^2-8z+1-i\)、\(f^{\prime}(z)=5z^4+4(3i+4)z^3-6iz^2+8z-8\)として、プログラムを走らせると。

となり、\(-0.025616321676689074+1.2619102215220996i\)という解が求まりました。上の図ではこれが本当に解になっているかどうか\(f(z)\)に入れて確認しています。\(f(-0.025616321676689074+1.2619102215220996i)\)\(=-3.4206564247796223\times 10^{-9}+9.118224397752783\times 10^{-8}i\)、であり、この絶対値は、\(9.124638352917773\times 10^{-8}\)。この絶対値はかなり\(0\)に近いので確かに五次方程式の零点を計算することができました!
なおこの零点を探索する過程での魚群探知機の探索履歴は以下のような図になります。どんどん、零点に迫っていっていることがわかるかと思います。
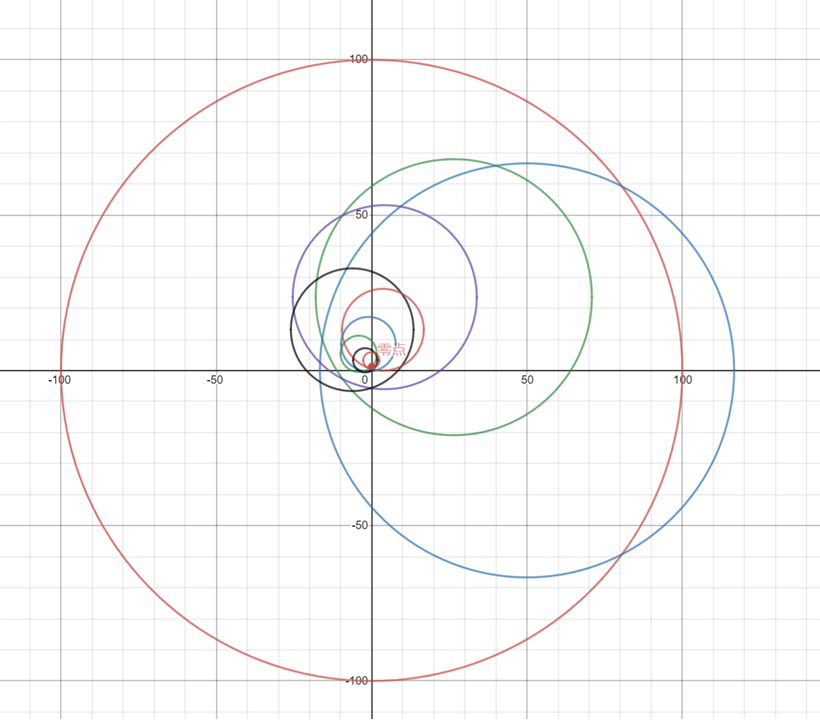
さいごに
今回は「偏角の原理」について紹介しましたが、私が偏角の原理に興味を持った理由はなんと素数が大好きだからです。素数は\(2\)、\(3\)、\(5\)、\(7\)、\(11\)、\(13\)、\(17\)、\(19\)、、、と続く数で、整数なのでもちろん飛び飛びです。
偏角の原理の主張には関数の微分や積分が入っており、これは言わば滑らかにつながった連続的な世界です。こんな飛び飛びで微分とかできそうもない整数、素数とは相性が悪いように思えます。しかし、数学の世界には解析的整数論という分野があり、そこでは飛び飛びの整数を、連続的で滑らかな複素関数を使って研究します。特に素数の研究に登場するのはゼータ関数と呼ばれる関数です。今回は五次方程式の零点を求めましたが、ゼータ関数の零点を調べることで素数の分布が分かるのです!
ゼータ関数の零点がどこにあるかという問題はリーマン予想と呼ばれ、160年以上に渡って数学者達が研究を行っています。偏角の原理はある領域内の関数の零点の個数がわかるということで、ゼータ関数の研究にも使われています。例えば1912年にバックルンドという数学者は偏角の原理を用いてゼータ関数の\(\frac{1}{2}+\tau i\,\,(0\leq\tau\leq 200)\)の形をした零点は\(79\)個であることを証明しています。こういった背景があり、素数、ゼータ関数の勉強をする中で偏角の原理のすごさを目の当たりにして本記事を書いた次第です。
五次方程式には解の公式は存在しないことを証明した代数学(ガロア理論)、偏角の原理が登場する複素関数論、素数の研究をする整数論達がこのように有機的につながっているのはとても面白いと思います。
明日はmath_nekoさんの「ふとしたきっかけで見つけた共線定理の話(外部サイト)」です!
参考文献
ゼータ関数の零点計算の歴史や手法が詳しく載っている
ゼータ関数入門書としておすすめ
結局ゼータになってしまった。。。
(文/松中)
















