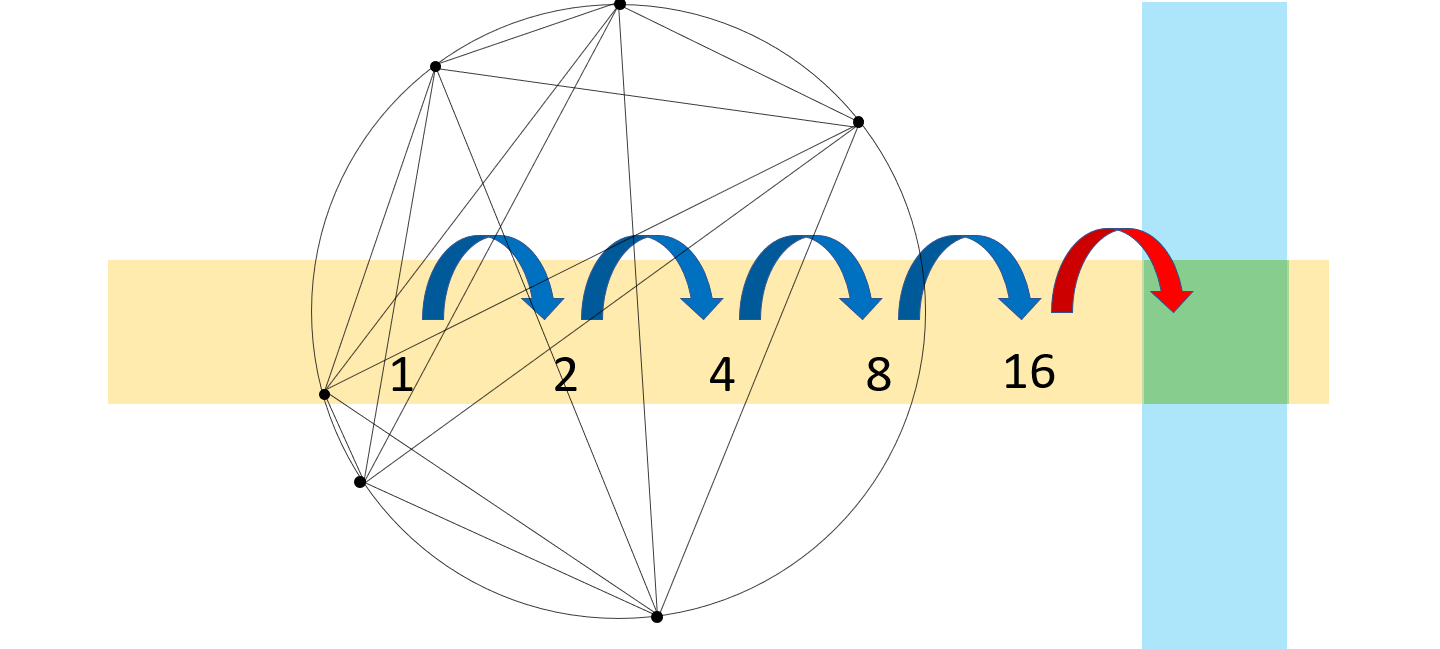
こんにちは。和からの数学講師の岡本です。今回は前回のマスログで扱った次の問題

に関連する話題についてお話しします。

１．レオ・モーザーからの出題

カナダの数学者レオ・モーザー(1921～1970)は次の問題を考えました。

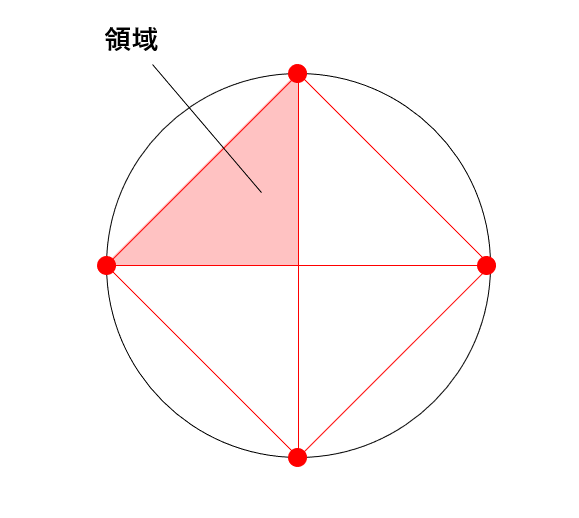
これは1969年にモーザーによって問題提起されたことから、「モーザーの問題」と呼ばれています。今回は\(n=6\)のときどうなるか考えてみることにします。

２．観察してみる

ひとまず、点の個数（\(n\)で表すことにします）の小さい方から順番に観察してみましょう。
たとえば、\(n=1\)のとき、円の内部には\(1\)の領域があります。\(n=2\)のとき、線を結ぶことで\(2\)つの領域に分かれます。

\(n=3\)のとき、図のように円内部は\(4\)つの領域に分かれ、\(n=4\)の場合、\(8\)つの領域となります。

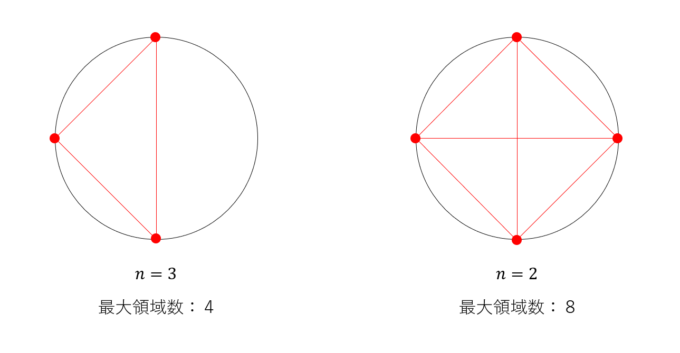
\(n=5\)の場合、やや線が多くなりますが、最大で\(16\)の領域に分けられることがわかります。

さて、点の個数を\(n\)、分けられる領域の個数を\(a_n\)とおき、ここまでの観察をまとめてみましょう。

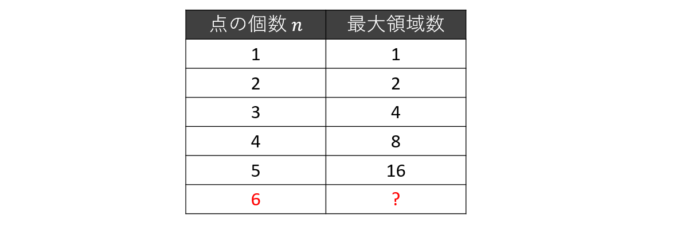
おや！？この流れは見覚えがありますね！

３．再び数字の規則の問題へ

さて、前節では円内部にできる領域の個数を観察しました。この流れは

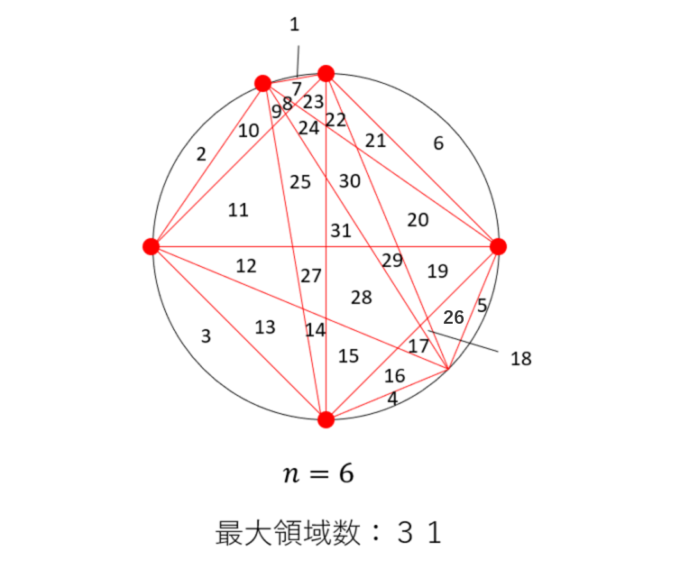
の問題と同じ流れとなっています。安易に考えると、次は\(32\)になることが予測されますが、果たして正しいのでしょうか？実際に\(6\)個の点で、領域を分けてみましょう。

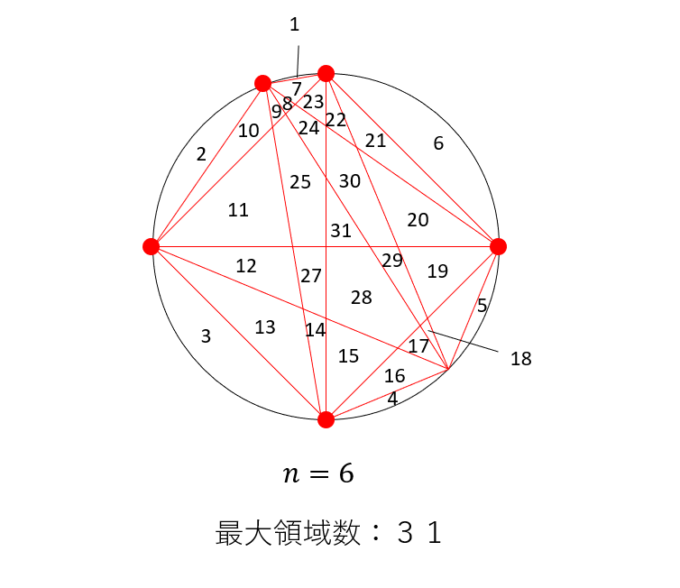
数えてみると、\(31\)の領域になっています。実はこれが最大の領域数となっています。
実は\(n=7\)のとき、最大\(57\)の領域に、\(n=8\)のとき最大\(99\)の領域に分かれることが知られています。このような数列\(a_n\)を提唱者にちなんでモーザー数列と呼びます。
なお、モーザー数列の一般項は以前のマスログで登場した“無理矢理予測モデル”

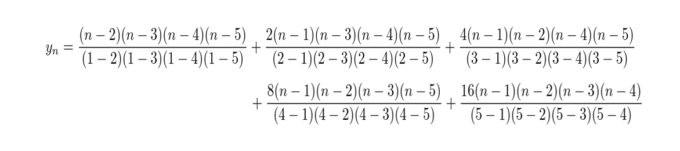
に一致します。つまり、ある意味で“実在する数列”だったわけです。

４．さいごに

いかがでしたか？世の中にはさまざまな数学の問題があふれかえっており、思わぬところで関係があったりします。むしろそういうところが数学の面白いところでもあります。
なお、このモーザー数列の一般項の導出について気になる方も多いかもしれないので、次回のマスログで解説してみることにします。お楽しみに！

和からではオンラインによる集団授業や個別授業も行っております。算数から数学、統計学まで幅広く対応していますので、興味のある方はまずは無料の個別カウンセリングへ！

和からの数学教室

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>