数字の予測~さあ次はどうなるでしょう?~
公開日
2020年12月19日
更新日
2020年12月19日
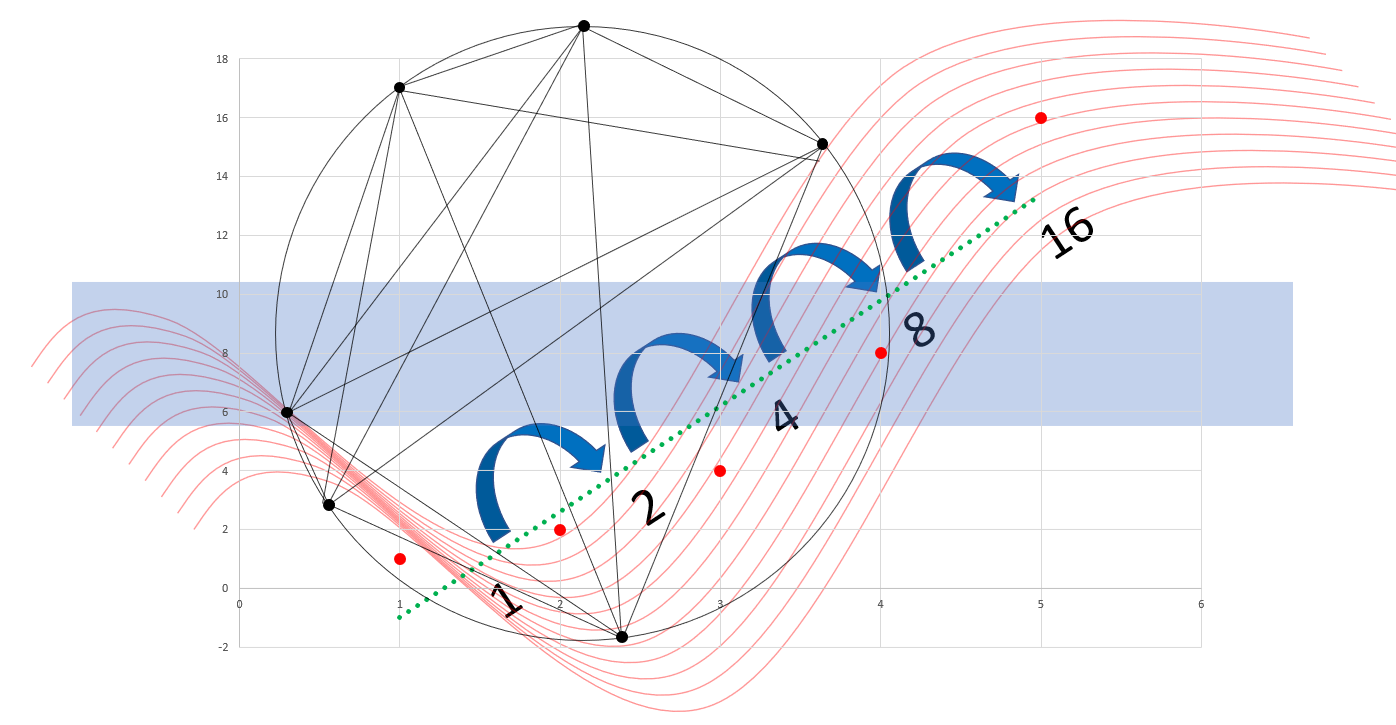
こんにちは。和からの数学講師の岡本です。今日は「数字の予測」というテーマでお話していきます。
たとえば次のような問題をご覧ください。
「規則」や「構造」を読み取って次にくる数字を予測するというもので、高校で習う「数列」の問題の導入などでも見かける類の問題です。果たしてどんな答えになるでしょうか?はたまた、答えは一つだけなのでしょうか?
この記事の主な内容
1.空気を読んで予測する
「数列の導入的な問題である」ということを踏まえて、「忖度」します。1, 2, 4という上がり方が足し算的なのか掛け算的なのかを考えます。差をみると1,2と値が変わっています。
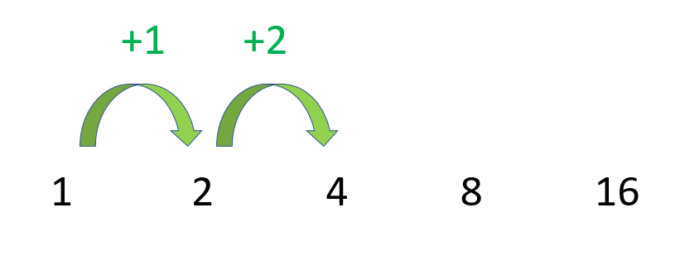
比を見ると、どちらも「2倍」の関係になっています。
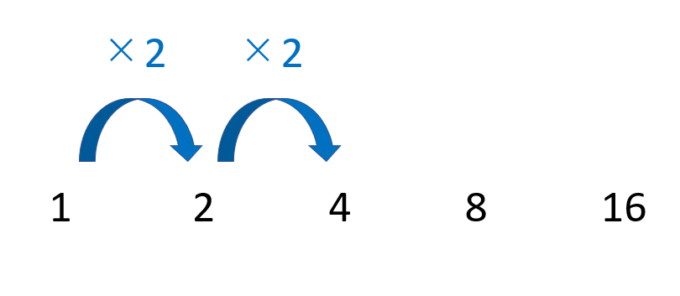
そこで、「2倍されているのではないか」と予想し、のこりの数で確かめます。
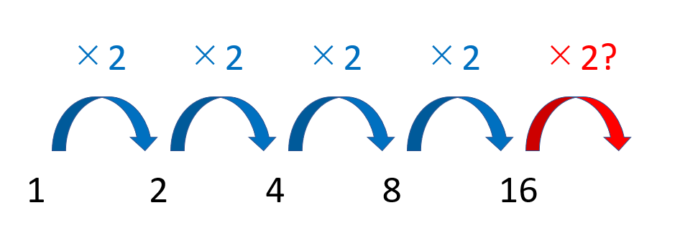
4, 8, 16。確かに「2倍」の関係が成り立っています。では16の次にくるのは\(16\times 2=32\)ではないかと予測できます。「答えは32です」
たぶん、「32」が想定されている答えだと思います。しかし本当に答えはこれだけでしょうか?
2.空気を読まずに予測する①
「予測」。それは統計学の基本的な目的の一つで、売上や株価など、今までの傾向や原因から予測モデルを作ることができます。最も基本的な予測モデルとして「回帰分析」というものがあります。実際に今回のデータを「回帰分析」してみましょう。
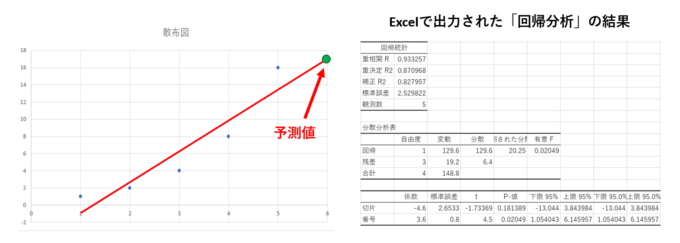
番号と値の散布図とこれらの点の関係を表す「最もあてはまりのいい直線」を示しました。回帰分析とは簡単に言うとこの直線を決定することです。
さあ、直線の式から\(y_n=3.6n-4.6\)という予測モデルが得られました。つまり、\(n=6\)とすると\(17\)であることが予測値として出力されました。「答えは17です」
3.空気を読まずに予測する②
上で示した「回帰分析」はあくまで「直線的な関係性」をベースに予測をするものです。実際に散布図をみると、点の配置はどちらかというとカーブを描いているように見えます。しかも、予測モデルの直線は元のデータ1, 2, 4, 8, 16全ての点を通っていません。これでは信憑性に欠けますね。そこで、「全ての点を必ず通る」ような、なるべく簡単な関数=多項式で予測をしてみましょう。実は非常に簡単な作り方があります。例えば、\(n=1\)を入れると\(a\)、\(n=2\)を入れると\(b\)、\(n=3\)を入れると\(c\)であるという条件全てを満たすように
\begin{align*}
y_n=\frac{a(n-2)(n-3)}{(1-2)(1-3)}+\frac{b(n-1)(n-3)}{(2-1)(2-3)}+\frac{c(n-1)(n-2)}{(3-1)(3-2)}
\end{align*}
というモデルを「無理矢理」作ることができます。確かに\(y_1=a, y_2=b, y_3=c\)となります。最初の問題をこの方法で\(y_n\)を作ると
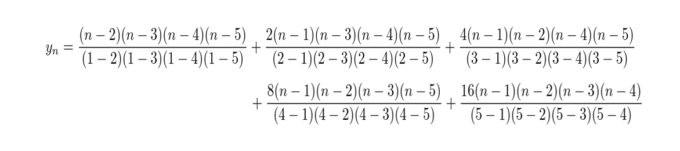
となります。この予測モデルに\(n=6\)を入れると\(31\)という値がかえってきます。「答えは31です」
※なお、この一見謎に見える予測モデル、実は非常に有名な数列でもあるので、別途マスログでご紹介します。
4.さいごに
いかがでしたでしょうか。たくさんの異なる回答が出てきましたが、どれも間違いではありません。「予測」をするというのは状況や目的によって変わってきます。つまり答えは1つではないのです。そのため、答えを1つにするには「どういう意図で予測するのか」ということを問題に明記するべきだと個人的には思います。しかしながら、あまり厳密すぎるのも良くないので、たくさんの「異なる答え」を否定せずに、その多様な考え方を共有することが重要なのだと思います。こういった学びかたは大人も子どもも共通なのです。
今回ご紹介した「回帰分析」。マーケティングやビジネスデータの分析で非常に良く使われる分析手法の1つですが、数学的な背景が難しく、数式を読み進めての理解は非常に困難です。和からでは、実際に「手で動かす」「体感する」をモットーに数式なしのデータ分析セミナーを開催しています。まずは無料のセミナーからお試しください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>













