こんにちは。和からの数学講師の岡本です。今回は、以前SNSで話題になった（？）、あるホテルのフリーWi-Fiのパスワードについてのお話です。

１．「この積分の最初の10桁がパスワードです」

まずはこちらをご覧ください。

海外のあるホテルや大学のラウンジにおけるWi-Fiのパスワードがこれです。
つまり、「積分せよ、さもなくばパスワードは渡さん。」というわけです。
とんでもないマスハラ（マスマティック・ハラスメントの略）ですね。。。！

２．積分の意味

まず、積分の意味を知っておく必要があります。積分は簡単に説明すると、以下のように中の関数の形をかたどった部分の面積を表します。

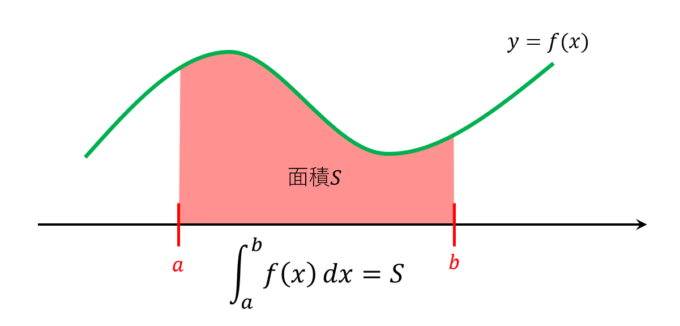
例えば、関数がマイナスの値にあるとき、「マイナスの面積」となります。

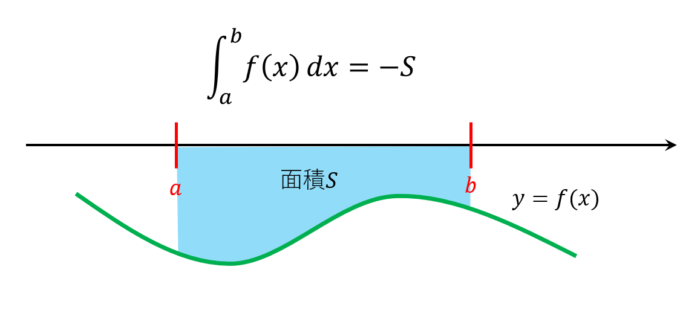
なので、以下のような関数の積分は面積が相殺されて0になってしまいます。

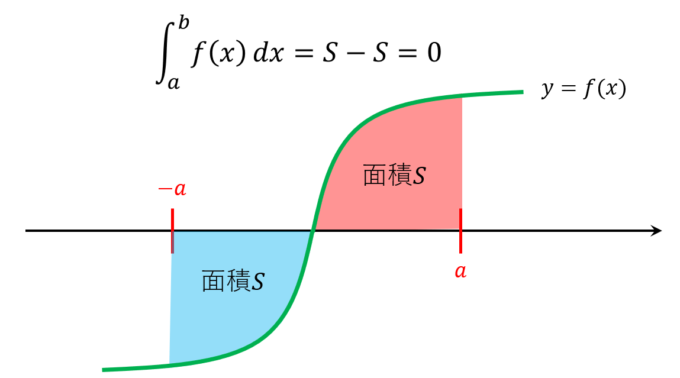
３．奇関数の積分

先ほどの図のように原点対称な形を描く関数は左右に同じだけ積分するとちょうど0になってしまいます。このような原点対称になる関数を「奇関数」といい、以下の等式で特徴付けられています。

$$\begin{align*} f(-x)=-f(x) \end{align*}$$

この場合$a>0$に対して

$$\begin{align*} \int_{-a}^{a}f(x)dx=0 \end{align*}$$

が成り立ちます。また

$$\begin{align*} f(-x)=f(x) \end{align*}$$

という性質の関数を偶関数と言います。さて今回話題になっている関数を見てみましょう。

$$\begin{align*} \left(x^3\cos \frac{x}{2}+\frac{1}{2}\right)\sqrt{4-x^2}=x^3\cos\frac{x}{2}\sqrt{4-x^2}+\frac{1}{2}\sqrt{4-x^2} \end{align*}$$

実は第１項は奇関数で後半は偶関数となります。つまり、パスワードに書かれている積分により前半の強そうな関数は0になっちゃうわけです。

$$\begin{align*} \int_{-2}^2\left(x^3\cos \frac{x}{2}+\frac{1}{2}\right)\sqrt{4-x^2}dx &=\int_{-2}^2x^3\cos\frac{x}{2}\sqrt{4-x^2}dx+\int_{-2}^2\frac{1}{2}\sqrt{4-x^2}dx\\ &=0+\int_{-2}^2\frac{1}{2}\sqrt{4-x^2}dx \end{align*}$$

４．円の面積

さて、結局は後半の積分がカギを握っています！

$$\begin{align*} \frac{1}{2}\int_{-2}^2\sqrt{4-x^2}dx \end{align*}$$

この関数$y=\sqrt{4-x^2}$は書き換えると

$$\begin{align*} y^2=4-x^2\Longrightarrow x^2+y^2=4 \end{align*}$$

となり、半径$2$の円の上半分を意味しています。

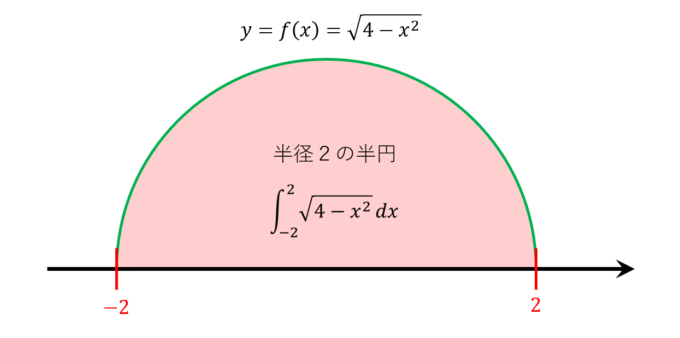
しかも積分区間もちょうど$-2$から$2$までなので、積分部分は「半径$2$の半円の面積」を表しています。これを$1/2$倍するので、結局「半径$2$の円の$1/4$の面積」が求める答えとなります！
つまり、$2^2\pi \div 4=\pi$となり、積分の答えは円周率$\pi$でした！
なお、円周率が答えになることはわかっていても、最初の10桁(3141592653)を知らないと入力できないという罠があります（岡本は100桁までは覚えているので安心です（?））。

４．さいごに

いかがでしたでしょうか？今回のパスワードは特殊ですが、思いもよらないところで数学で出てくることがあります。そういった数学や計算力、算数力を鍛える機会も少ないですが、和からでは大人の数学・算数の学び方ということで個別教室から集団授業までを展開しています。興味のある方は是非一度無料の個別カウンセリングへ！

和からの数学教室

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>