PowerPointを用いた美しい比率のアート~後編~
公開日
2023年11月17日
更新日
2023年11月17日
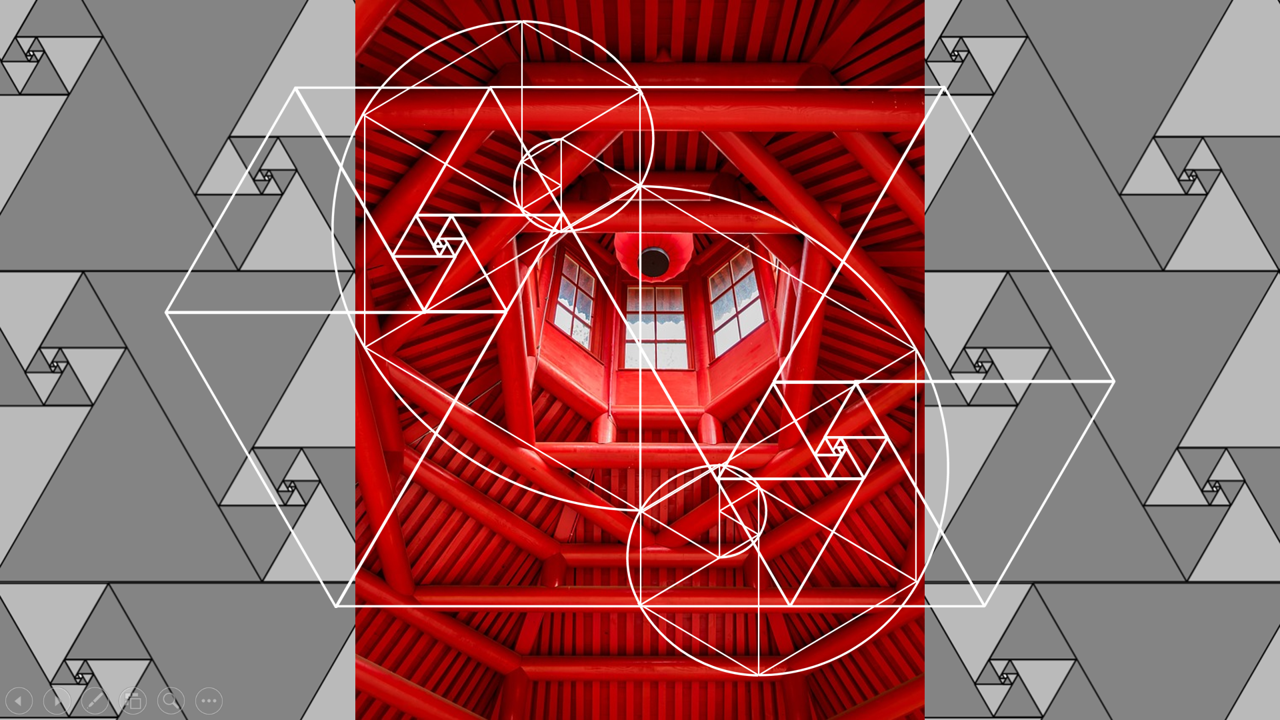
みなさんこんにちは!和からの数学/算数講師の岡本です。今回は前回に引き続き、図形の特殊な比率に関して簡潔にまとめていこうと思います。
この記事の主な内容
1.図形の比率とデザイン
長方形の縦と横の比率について考えてみましょう。比率が1:1、つまり同じ場合、「正方形」になります。正方形を2つ並べることで、1:2の長方形ができます。さらに、大きい辺の長さを一辺にもつ正方形をくっつけることによって、2:3の長方形ができ、さらに同じ操作を繰り返すことで、5:3、8:5、13:8という比率の長方形が出来上がります。
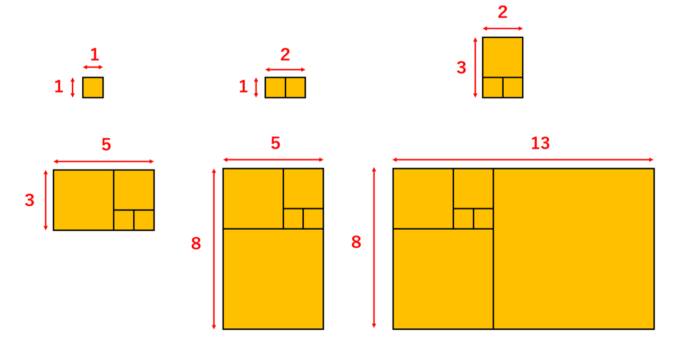
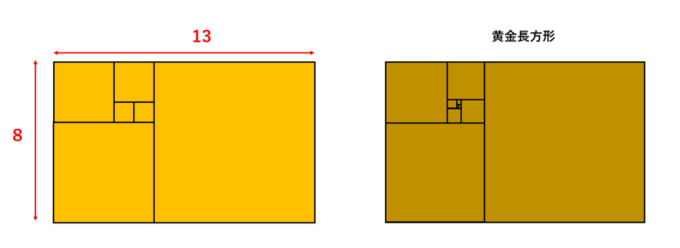
これらの正方形の一辺の長さからできる数字の列「1,1,2,3,5,8,13,…」はフィボナッチ数列といい、不思議な性質をたくさん持っています。その1つに、「隣り合うフィボナッチ数の比は、黄金比に近づく」という性質があります。つまり、先ほど作成した長方形は隣り合うフィボナッチ数の比であるので、操作を繰り返していくことで「黄金長方形」に近づきます!(前回の記事参照)
また、黄金比を一般化した「白銀比」や「青銅比」というものも知られています。白銀比に関しては2種類あり、用紙のサイズに応用される\(1:\sqrt{2}\)のものと、黄金比の定義を一般化した\(1:1+\sqrt{2}\)のものがありますが、どちらも美しい性質を持っています。特に\(1:1+\sqrt{2}\)の白銀比は、正八角形と関連があり、これを用いたデザインも考えられます。
2.プラスチック比
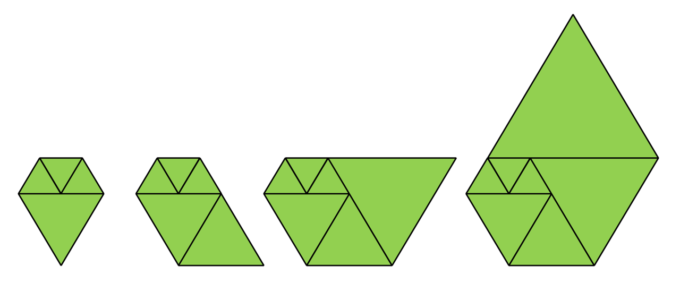
さて、先ほどは正方形をぐるぐる並べていき、大きな長方形を作っていく作業の中にフィボナッチ数が現れるというお話がありましたが、今回は正三角形を考えてみましょう。まず、正三角形を1つ用意し、同じサイズのものを隣にくっつけます。また。もう一つ同じサイズの三角形をくっつけて図のような台形にします。
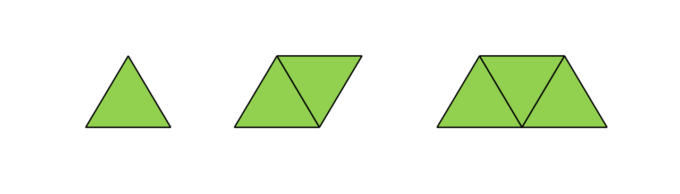
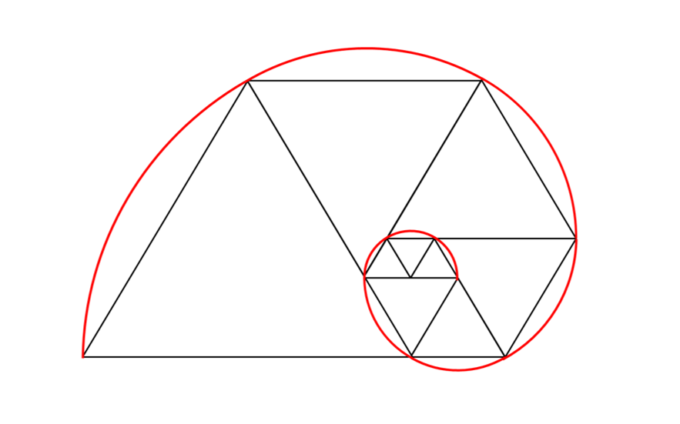
次に、この台形の一番長い辺を一辺にもつ正三角形を貼り合わせて、図のような五角形にし、同じサイズの正三角形を使って、五角形を作ります。ここから同じように「ぐるぐる」と回すように正三角形をくっつけていき、五角形を成長させます。このような辺の長さの列「1,1,1,2,2,3,4,5,…」をパドヴァン数列といい、その比はプラスチック比と呼ばれる数字に収束することが知られています。つまり、フィボナッチ数列の三角形版はパドヴァン数列で、黄金比に対応しているのがプラスチック比となり、美しい数学的な関係が現れます。
3.デザイン例
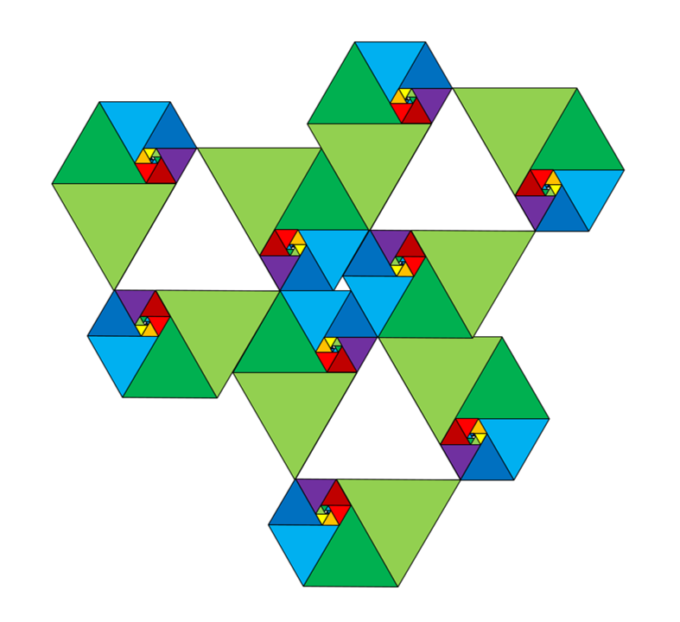
実際にプラスチック比を用いたデザインを考えてみました。黄金比と同様に正三角形が無限に続く構造を持っており、非常に美しいです。

4.さいごに
いかがでしたでしょうか?今回はあまり具体的な比率や作成方法には触れずに比率を使ったデザイン案や関係性について触れていきました。より詳しい内容に関しては2023年11月26日(日)の17:00~18:30に開催される数学アートセミナーにて実際の数式やPowerPointを用いた作成方法をお話します!興味のある方はぜひご参加ください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>














