はじめに

大人のための数学教室和(なごみ)の講師の松中です。最近印象に残った授業シリーズとして不定期に授業の内容を紹介していきたいと思います。今回紹介したいのは三角形の重心に関してです。

なおこちらの記事の内容は動画でも解説しています。

物理学の公式を用いた三角形の重心の計算

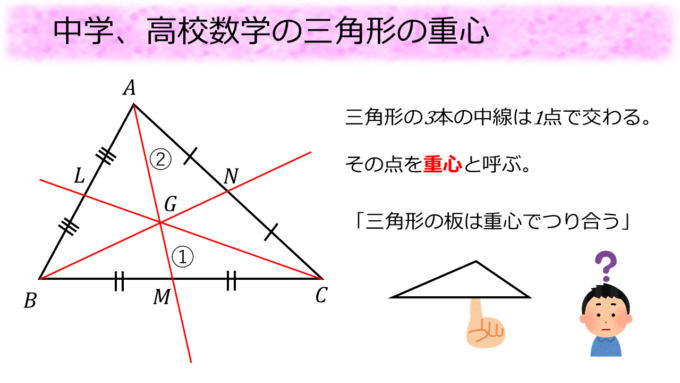
中学や高校では三角形の重心を「3本の中線の交点」として定義します。

中線とは三角形の1つの頂点と向かいにある辺の中点を通る直線のことです。三角形には3本の中線がありますが、この中線が1点で交わることを証明した後に、その交点に「重心」と名前を付けているのです。

ここでなぜその点に「重心」と名前を付けているのかに関してはあまり言及はないように思えます。言及していたとしても、「三角形の板をくりぬいたとき、指の上に重心が来るように三角形を乗せるとつり合う」くらいの話しか書いていません。つまり、なぜ重心でつり合うのか、という説明はありません。

重心はその定義から三角形の真ん中というイメージはありますが、だからといって重心で三角形の板がつり合うと言い切るのは短絡的な発想です。実は物理の世界でのつり合いの条件から三角形の重心は確かにつり合う点だということが確認できます。

今回の授業が印象に残った理由ですが、お客様に中学、高校数学の定義で三角形の重心の解説をした際に、なぜそこを重心と呼んでもよいのかという質問をされ、物理の世界の公式から実際に三角形の重心を計算したからです。中学高校のテキストには載っていないような話かと思います。

さて、重心は頂点とその対辺の中点を結ぶ線分を\(2:1\)に内分することは高校数学のテキストに載っています。その事実から、三角形を\(xy\)平面におき、各頂点の座標を\(A(a_x,a_y)\)、\(B(b_x,b_y)\)、\(C(c_x,c_y)\)としたときに、\(\triangle{ABC}\)の重心\(G\)の座標は、
\[
G\left(\frac{a_x+b_x+c_x}{3},\frac{a_y+b_y+c_y}{3}\right)
\]
で与えられることがわかります。これは後で物理の公式から重心を求める際に確かに中学高校テキストの定義から求まる重心と同一であることを確認するために使う事実になります。

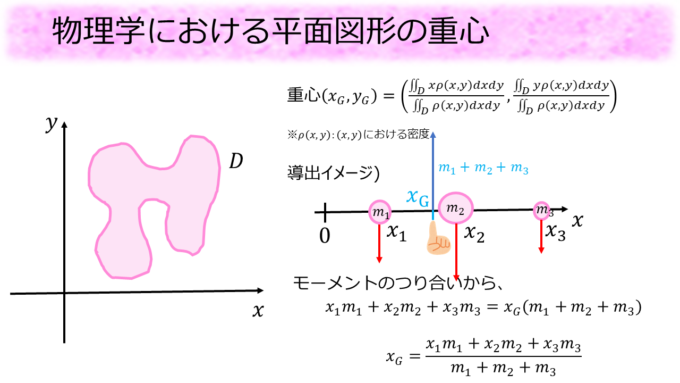
さて物理の世界における重心公式を紹介しましょう。\(xy\)平面上の2次元図形\(D\)について考えます。この図形\(D\)の密度(単位面積当たりの質量)を\(\rho(x,y)\)と置くとき、図形\(D\)の重心\((x_G,y_G)\)は、
\[
(x_G,y_G)=\left(\frac{\iint_Dx\rho(x,y)dxdy}{\iint_D\rho(x,y)dxdy},\frac{\iint_Dy\rho(x,y)dxdy}{\iint_D\rho(x,y)dxdy}\right)
\]
で与えられます。

何とも複雑で難しそうな式ですね。図形が一様、つまり場所よって密度が変わらない場合は、\(\rho(x,y)=1\)として消してしまってよいのでやや見やすくはなります。そして、\(\iint_D\)は重積分と呼ばれる積分になり、これは大学で学ぶことになります。

この公式の導出ですが、イメージとして一次元上に複数の質点がある場合の一般化(高次元化、連続化)と考えれば難しくはないのですが、ここでは割愛します。

さて実際にこの重心の公式を使って三角形の重心を求めてみましょう。今回は\(A(a,b)\)、\(B(0,0)\)、\(C(c,0)\)を頂点とする\(\triangle{ABC}\)について考えます。ここで\(a,b,c>0\)であり、\(c > a\)とします。また、密度は場所に依らず一定ということで\(\rho(x,y)=1\)とします。

都合の良いように三角形を設定していますが、どのような三角形も回転と平行移動、裏返しを行うことで\(B\)を原点に、\(C\)を\(x\)軸上に移動できますのでご容赦ください。また\(a>c\)の場合も同じように計算できるので、重心を計算できるように強い仮定を置いているわけではありません。

さて、このように\(\triangle{ABC}\)を設定したときに、中学高校の公式から求まる三角形の重心は、
\[
\left(\frac{a+c}{3},\frac{b}{3}\right)
\]
となります。

物理の公式から重心を計算して上の座標と一致したら成功ということになります。

重心の計算は以下に書いてある通りですが、計算にあたっていくつか補足説明をしておきます。

まず重積分を累次積分で計算するため、領域\(D\)を\(0\leq x \leq a\)の部分と、\(a\leq x\leq c\)の部分の2つに分けて計算しています。

また、分母の
\[
\iint_Ddxdy
\]
は\(D\)の面積そのものなので、重積分を計算してなくても算数で習う三角形の面積の公式から\(\frac{1}{2}bc\)であることがわかります。

実際に分母、\(x\)座標の分子、\(y\)座標の分子を計算すると上のようになり、結果以下のように\(\triangle{ABC}\)の重心が求まります。

たしかに、中学高校数学の重心の公式から求まる点の座標と一致していますね！めでたしめでたし。

まとめ

今回は三角形の重心を中学高校で学ぶイメージからではなく、物理の世界の背景から計算してみました。今回は図形\(D\)の密度を一定としましたが、\(\rho(x,y)\)を適切に設定することで、例えば、左から右に進むにつれて材質が木材から金属にゆっくり変わっていく、といった不思議な三角形の重心なども計算できます。

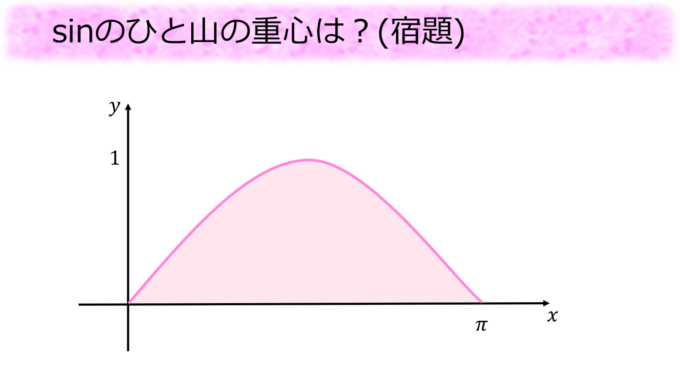
今回紹介した公式を使えば\(\sin\)の一山の重心も計算できるので、宿題として出してみたいと思います。図の対称性から重心の\(x\)座標は\(\frac{\pi}{2}\)になりそうですね。また重心の\(y\)座標は半分の高さ\(\frac{1}{2}\)より少しだけ小さくなりそうですよね。実際に計算して確かめてみてください。

物理的な意味から重心を計算したい方はこちらの講座がおすすめです。

力学

(文/松中)

レイメイ藤井 見やすい白黒三角定規 黒10cm