平行曲線を数式を使って考えてみる

ロマンティック

公開日

2021年3月5日

更新日

2021年3月5日

こんにちは。和からの数学講師の岡本です。以前「平行曲線」について記事を書きました

今回は、数式を使ってがっつり考えていきます。

この記事の主な内容

１．平面上の曲線とパラメータ表示

平面に描く曲線でなじみ深いのが、放物線です。そのほかにも、円やサイン・コサインなどの波の曲線もよく見かけます。基本的に $xy$ 平面に直線や曲線を描く場合、 $y=f(x)$ という関数の情報があれば $x$ に1や2、3と数字を入れるだけで、 $y$ の値が計算でき、点 $(x, f(x))$ がプロットされていきます。つまり、「曲線」とは $(x, f(x))$ のペア全体で表されます。これをもう少し一般化すると「 $x$ と $y$ の関係」の情報があれば、平面上に図形が描けるというわけです。そこで、第3の変数 $t$ を使って、例えば $x(t)=\cos t, y(t)=\sin t$ としてみます。このとき、点 $(x(t), y(t))$ は変数 $t$ で支配されており、 $t$ の値を動かすと、平面上の点 $(x(t), y(t))$ が動きます。

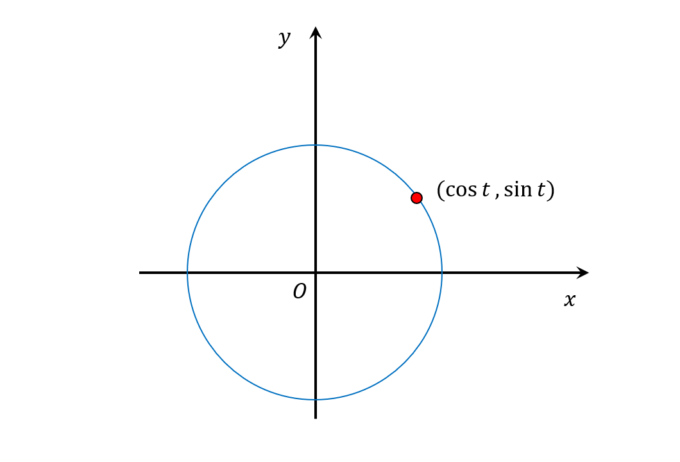
実際に $x(t)=\cos t, y(t)=\sin t$ とした場合、上の図のように半径1の円が描かれます。このように、平面上の曲線 $C$ を変数 $t$ で統制できるとき、この $t$ を、曲線 $C$ のパラメータといい、 $x(t)=\cos t, y(t)=\sin t$ のように、 $x$ 座標と $y$ 座標を $t$ を使って表す表示をパラメータ表示といいます。以降は $t$ を「時間」とし、一般のパラメータ表示 $(x(t), y(t))$ を扱っていくことにします。

２．平行曲線と曲率

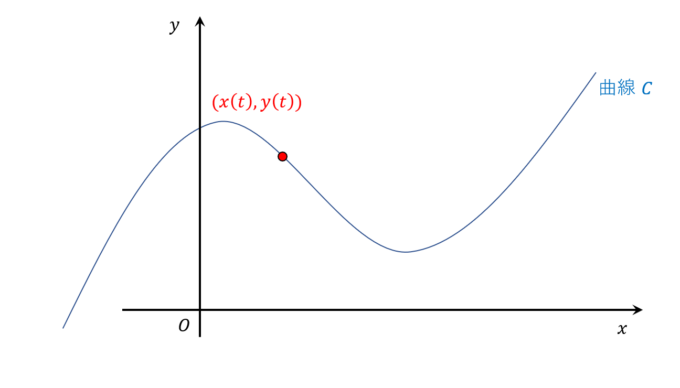
ここではパラメータ表示 $(x(t), y(t))$ をもつ曲線 $C$ を考えます（ $\vec{c}(t):=(x(t),y(t))$ とおきます）。時刻 $t$ における傾きを表すベクトルは微分をすることで $(x'(t), y'(t))$ となります。また、この方向に直交するベクトルは、内積が $0$ であるように例えば $(-y'(t), x'(t))$ と設定することができ、これを時刻 $t$ における法線ベクトルと言います。

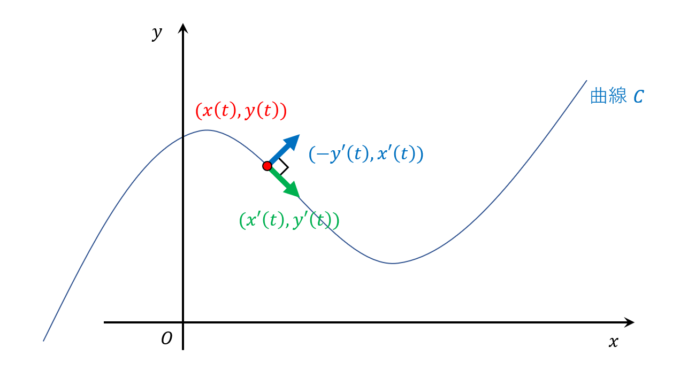
これから、法線ベクトルの長さの調節を行いたいので、どんな時刻 $t$ に対しても常に長さを $1$ になるようにします。方法は簡単で、法線ベクトルの長さで割ればいいだけです。こうしてできたベクトルを単位法線ベクトルといい、 $\vec{n}(t)$ で表すことにします。

$\begin{align*} \vec{n}(t)=\frac{1}{\sqrt{x'(t)^2+y'(t)^2}} \left( \begin{array}{c} -y'(t) \\ x'(t) \end{array} \right). \end{align*}$

こうして、曲線 $C$ の時刻 $t$ における法線方向に $d$ 離れた位置は $\vec{c}(t)+d\cdot\vec{n}(t)$ と表すことができます。つまり、曲線 $C$ から距離 $d$ 離れた平行曲線 $C_d$ のパラメータ表示 $(x_d(t),y_d(t))$ は

$\begin{align*} \begin{cases} x_d(t)=x(t)-\frac{d\cdot y'(t)}{\sqrt{x'(t)^2+y'(t)^2}}\\ y_d(t)=y(t)+\frac{d\cdot x'(t)}{\sqrt{x'(t)^2+y'(t)^2}} \end{cases} \end{align*}$

となることがわかりました。

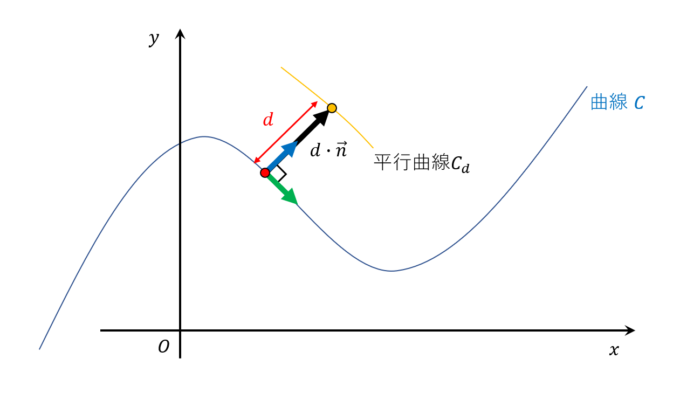
また与えられたパラメータ表示 $x(t),y(t)$ に対して、

$\begin{align*} \kappa(t):=\frac{x'(t)y^{\prime\prime}(t)-y'(t)x^{\prime\prime}(t)}{(x'(t)^2+y'(t)^2)^{3/2}} \end{align*}$

という関数を定めます。これは曲率といってその時刻における「曲がり具合」を表す指標です。曲線 $C$ の時刻 $t$ における曲率を $\kappa(t)$ としたとき、上で定めた平行曲線 $C_d$ の時刻 $t$ における曲率 $\kappa_d(d)$ には

$\begin{align*} \kappa_d(t)=\frac{\kappa(t)}{1-d\kappa(t)} \end{align*}$

という公式が知られています。

３．コサイン・カーブの平行曲線を計算してみる

具体的な曲線としてコサイン・カーブ $y=\cos x$ の場合を考えてみましょう。

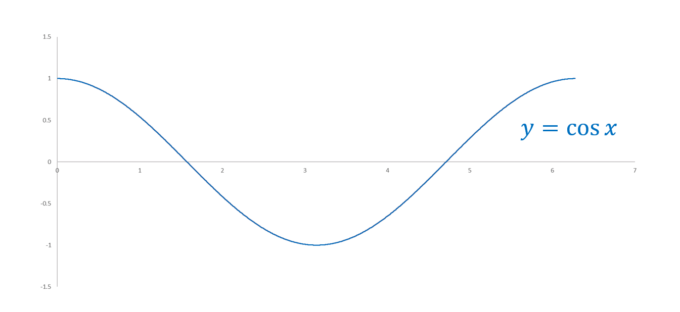
コサイン・カーブは $y=\cos x$ で表されますが、パラメータ表示として $x(t)=t, y(t)=\cos t$ と考えることもできます。 $x'(t)=1, y'(t)=-\sin t$ なので、先ほどの話に従い、距離 $d$ 離れた平行曲線 $C_d$ のパラメータ表示は

$\begin{align*} \begin{cases} x_d(t)=t+\frac{d\cdot \sin t}{\sqrt{1+\sin^2t}}\\ y_d(t)=\cos t+\frac{d}{\sqrt{1+\sin^2t}} \end{cases} \end{align*}$

となります。実際に $d=0.5$ の場合の平行曲線はこの式を使って以下のように描くことができます。

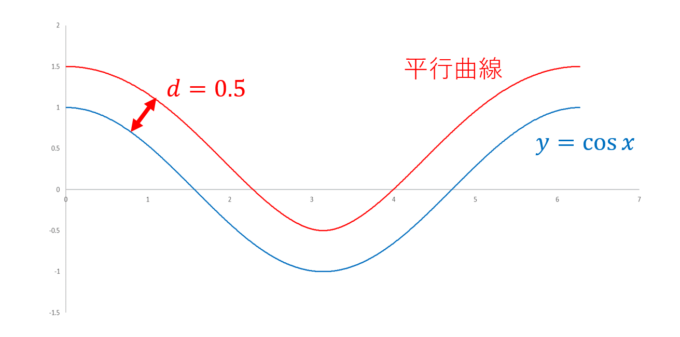
次に、コサイン・カーブの曲率 $\kappa(t)$ を求めてみましょう。曲率の定義に従って計算すると

$\begin{align*} \kappa(t)=\frac{-\cos t}{(1+\sin^2 t)^{3/2}} \end{align*}$

となります。距離 $d$ を $0.2, 0.5, 0.7$ として $\kappa(t)$ と $\kappa_d(t)$ の変化を表したのが以下のグラフになります。

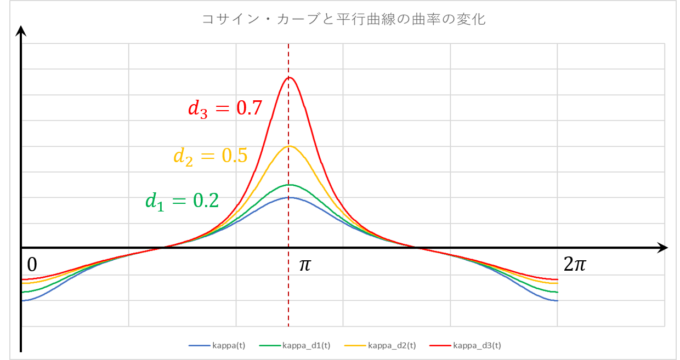
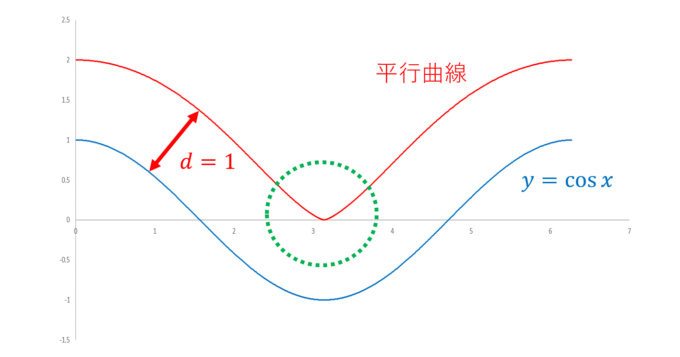
グラフからもわかるように、 $d=1$ に近づくにつれて $t=\pi$ における曲率が急上昇することがわかります。実際に $t=\pi$ での曲率は

$\begin{align*} \kappa_d(\pi)=\frac{1}{1-d} \end{align*}$

となり、 $d=1$ で曲率は無限大に発散します。曲率が無限になるということは、極端な曲がり＝「折り曲げ」が発生することを示します。実際に $d=1$ でコサイン・カーブの平行曲線に“異変”が起こっていました。

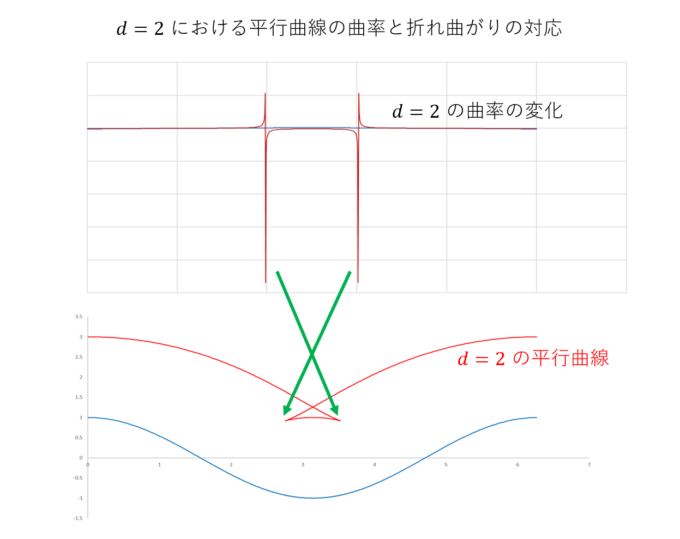
その後、 $d$ を1より大きくすると、無限大に発散する点が2つになり、平行曲線が2回折れ曲がる様子に対応します。

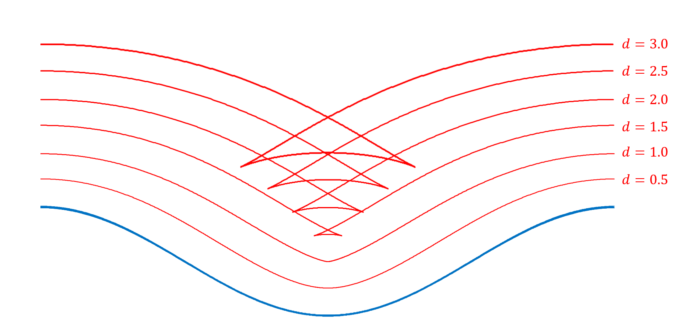
こうして、 $d$ を大きくすることで平行曲線は大きく折れ曲がった線となることがわかります。

４．さいごに

いかがでしたでしょうか。今回がパラメータ表示や微分、曲率といったやや高度な数学を使った考察を行ってきました。しかし、しっかりと数式で追うことで、折れ曲がるという現象発生のメカニズムを考察することができました。そう考えると、やはり数学は素晴らしいですね！なお、今回カーブを描くのに使用したのも前回同様Excelです。Excelはうまく活用すれば、いくらでも模様やグラフを描くことができます。Excelを使った図形作成のセミナーとして「Excelアートセミナー」があります。月1回で様々な模様やアートをExcelで描いていくので、興味のある方は是非ご参加ください。

なお、今回の内容（微分や曲率と言う概念など）に関するオススメの本はこちらです。微分幾何学の入門書として定番です。

曲線と曲面(改訂版) -微分幾何的アプローチ
梅原雅顕,山田光太郎(著) 裳華房