【徹底解説】数学×切り絵―4次元に住む龍―

ロマンティック

公開日

2020年10月18日

更新日

2020年10月18日

こんにちは。和からの数学講師の岡本です。何を隠そう、切り絵のアーティスト活動を行っており、モチーフに数学を積極的に取り入れています。これまでたくさんに作品を創ってきましたが、モチーフに関してよく尋ねられることがある「4次元に住む龍」について簡単に解説していこうと思います。

この記事の主な内容

１．多重切り絵

この作品の大きな特徴として、複数のアクリル板で切り絵を挟むことで立体感を出しています。私はこのような手法・作風を多重切り絵と呼んでいます。通常は切った紙を2枚のアクリル板に挟み展示することが多いですが、この作品に関してはアクリル板を20枚使用しています。

もちろん、切り絵の配置や、何枚目にアクリル板にどの切り絵を挟むかも事前に計算しています。そのためこの作品は切るまでの構想段階が非常に長い印象でした。

２．次元と球面

タイトルにある「4次元」とは一体何なのか。このような質問をよく頂きます。ポイントとなるのは真ん中にある丸い物体（の集合体）です。実はこの部分が4次元空間内の「球面」を表しています。私たちの住んでいる世界は通常3次元の空間をなしており、この世界における「球」とは、いわゆるボールを意味します。

もう少し正確に言うと、中が詰まっている球の事を「球体」、中身が空洞になっているものを「球面」と呼びます。例えば空気を入れて膨らませたボールは「球面」であり、3次元の世界で実現できます。しかし球面自体はあくまで「面」であることから、このような球面は「2次元球面」と呼ばれ、しばしば\(S^2\)と表します。

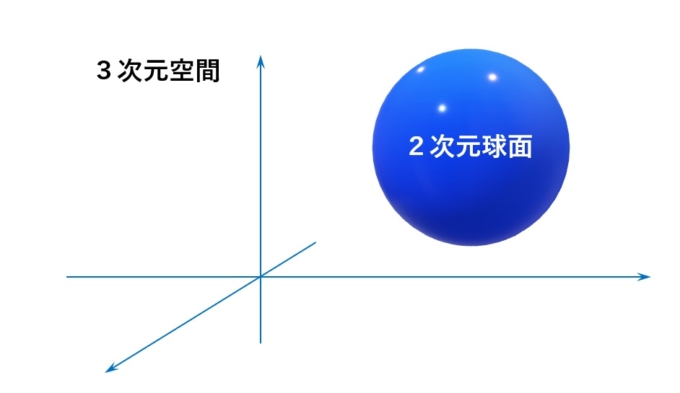
１つ次元を落としてみましょう。「1次元球面」というものもあり、これは2次元平面内における「球面」となります。この1次元球面\(S^1\)の正体は「円」です。実は平面の世界での「球」は「円」なのです。

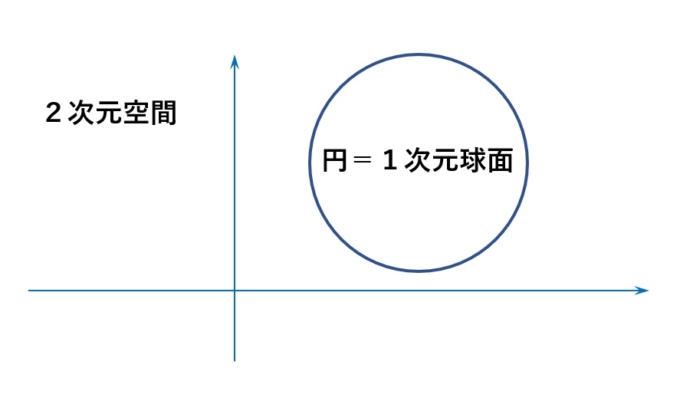
また１つ次元を下げてみましょう。1次元世界とは1つしか軸を持たない、つまり線上の世界を表しています。この世界の「球面」とは何なのでしょう？実は各次元の球について下図のような面白い関係があります。

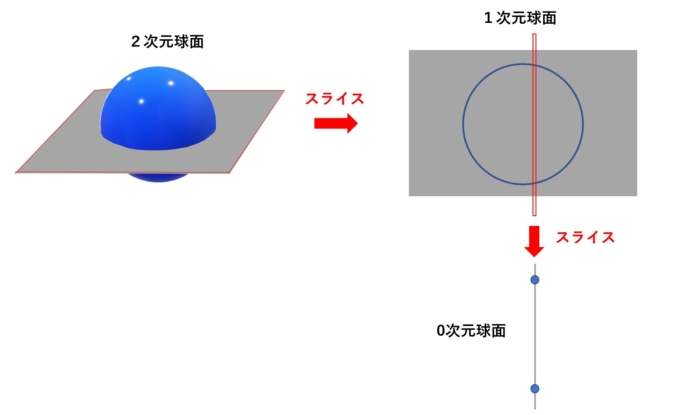
「2次元球面」をスライスしたときの断面は「円」となります。つまり１つ次元の下がった「1次元球面」となるわけです。この関係性は一般の次元でも成り立ち、「1次元球面の断面は0次元球面」となるのです！
それを踏まえると、「0次元球面」とは円をスライスすることでできる「2つの点」となります。なんと、「0次元球面」とは「2つの点」の事だったのです！

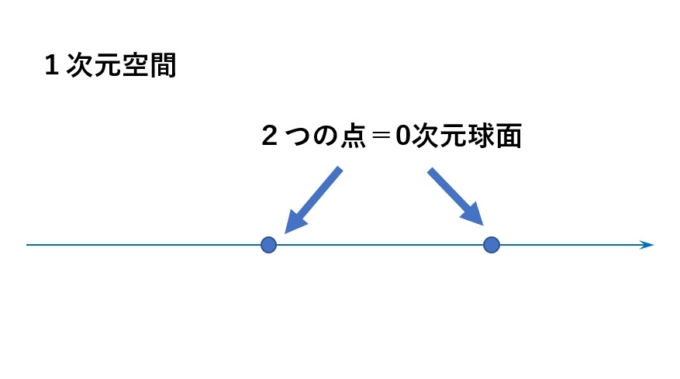
３．4次元球面

では、高い次元に対して考えてみます。前節の考察の通り、スライスすることで次元が１つ下がります。つまり4次元の世界の球面＝「3次元球面」の断面は「2次元球面」＝ボールとなります。通常4次元の世界でないと実現できない「3次元球面」ですが、スライスすることで3次元空間のボールが出来上がります。奥行きや工夫を凝らすことで3次元の物体を平面上に描写できます（数学的には、これを2次元空間への射影と考えます）。

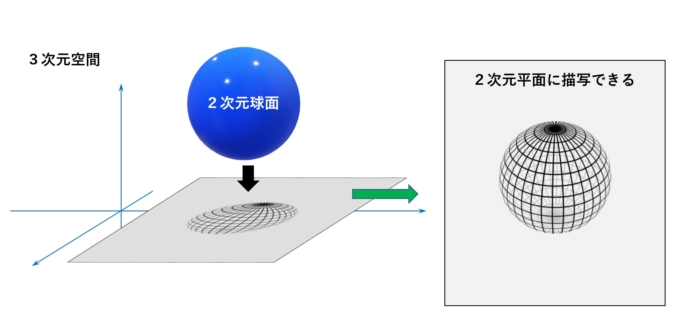
これを応用します。「3次元球面のスライス」である2次元球面を平面内に描写し、これらを複数重ねることで3次元球面を“無理やり”表現することができます。それが作品の意味する「4次元」です。

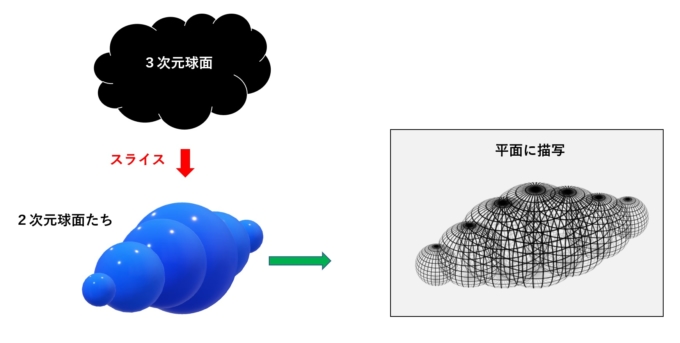
「龍はこの4次元の世界に生き、空間や時間を自由に行き来することができる」。そういった“自由の象徴”を意識して制作しました。

４．数式を使った表現

前節の話を数式を使って考えてみましょう。半径1の球面というのは\(x,y,z\)を使って以下のように表現できます。

\begin{align*}x^2+y^2+z^2=1\end{align*}

つまり、2次元球面\(S^2\)というのは集合として以下のようになります。

\begin{align*}S^2=\left\{(x,y,z)\in \mathbb{R}^3\mid x^2+y^2+z^2=1\right\}\end{align*}

この図形に関して平面\(z=t\)（\(-1\leq t\leq1\)）でスライスした図形\(S^2_t\)は以下のようになり、これは半径\(\sqrt{1-t^2}\)の1次元球面を表します。

\begin{align*}S^2_t=\left\{(x,y)\in \mathbb{R}^2\mid x^2+y^2=1-t^2\right\}\end{align*}

同様に4次元空間\(\mathbb{R}^4\)内の「3次元球面\(S^3\)」は

\begin{align*}S^3=\left\{(x,y,z,w)\in \mathbb{R}^4\mid x^2+y^2+z^2+w^2=1\right\}\end{align*}

と表され、先ほどと同様に\(w=1\)でスライスした断面は半径\(\sqrt{1-t^2}\)の2次元球面となります。

\begin{align*}S^3_t=\left\{(x,y,z)\in \mathbb{R}^3\mid x^2+y^2+z^2=1-t^2\right\}\end{align*}

５．さいごに

いかがでしたでしょうか。今回は切り絵の数学的な解説を行ってきました。他にも数学をモチーフにした切り絵作品はたくさんあるので、今後も気が向いたら少しづつ解説していこうと思います。なお、今までの作品や数学デザインのグッズに関してはこちらのページにまとめてありますので、興味のある方はご覧ください（https://wakara.co.jp/cut_and_math）。また、岡本の切り絵作品は以下のアートブックでも掲載されています。こちらも興味にある方はご覧ください。