アクチュアリー数学合格体験記
公開日
2020年10月20日
更新日
2020年10月20日

数学教室和(なごみ)講師の松中です。
今年もアクチュアリー試験が実施される12月が迫ってきましたね!
と言ってもそもそもアクチュアリーの事を知らない方が大多数ではないでしょうか。アクチュアリーは日本語では「保険数理人」と訳される保険、金融などの分野の数理業務を扱うプロフェッショナル職のことです。アメリカでは2015年のThe Best Jobs of 2015で200業種中1位になるほど人気の職業です(http://www.careercast.com/jobs-rated/best-jobs-2015)。
テレビCMを見ると生命保険、医療保険、火災保険、事故保険など様々な保険が宣伝されています。同じ医療保険でも保険会社によって掛け金、保障内容は様々です。それらの保険を作ることは簡単ではありません。顧客をたくさん獲得しようと掛け金を少なくし、保障を多くすればたちまち保険会社は潰れてしまうでしょう。また逆に保険会社が儲けるために掛け金を多くすると顧客が集まらずにやはり保険会社は潰れてしまいます。実際、17世紀のヨーロッパで生まれた初期の生命保険も、安易に掛け金、保障金を設定してしまったために、10年も待たずに制度が崩壊してしまったそうです。
そこで活躍するのがアクチュアリーです。アクチュアリーは確率・統計を駆使することで不確実な未来に向き合い、適切な掛け金、保障を設定します。ある男性が1年以内に亡くなるかどうかがわからなくても、50歳の男性10万人が1年以内に何名なくなるかはある程度予測できるのです。これが確率、統計の力です。
過去のマスログ記事で、アクチュアリーがどのような考えで保険料を決めているのかを簡単に解説しております。こちらも合わせてお読みください。
アクチュアリーになるためには日本アクチュアリー会が運営する試験に合格し、アクチュアリー会の正会員になる必要があります。
まずは、以下の5つの基礎科目全てに合格することで準会員になることができます。
- ・数学
- ・生保(生命保険)
- ・損保(損害保険)
- ・年金
- ・KKT(会計、経済、投資理論)
その後、以下のいずれかのコースで2科目合格することで晴れて正会員になることができます。
- ・生保コース:生保1、生保2
- ・損保コース:損保1、損保2
- ・年金コース:年金1、年金2
アクチュアリーは準会員になるまでには平均5年、正会員になるまでには平均8年かかると言われているほど、難関の資格なのです。
私は2018年と2019年に基礎科目の数学を受験し、2018年は不合格でしたが、2019年は何とか合格することができました。前置きが長くなりましたが、本記事では私がどのように勉強したのかを紹介したいと思います。
この記事の主な内容
私の作戦、対策方針
アクチュアリー試験の「数学」は小問集からなる第1問(全12問、各点5点、計60点)、確率を扱う第2問(20点)、統計を扱う第3問(20点)からなり、60点が合格ラインになります。
私の作戦はこうでした。
「第1問の小問集で満点の60点を狙う、しかし実際には満点は取れないだろうから、60点から足りない点数を第2問、第3問で拾う。」
第1問の小問集をターゲットにした理由は対策がしやすいからです。アクチュアリー試験は公式に大量の過去問が公開されています。なんと昭和37年実施分からあります。しかも解答付きです!
過去問の第1問(小問集)を眺めると、同じようなパターンの問題が何度も出ていることが分かります。小問を繰り返し解き、出題パターンに慣れることがそのまま対策になります。
一方、第2問、第3問は毎年重めの式変形の穴埋め問題であり、点数に直結するような対策が思いつきませんでした。過去問をこなすのに時間がかかる割には、実りが少ない問題達とも言えます。第2問、第3問は、普段からどれだけ複雑な数式変形をしているか、確率、統計の公式にどれだけ慣れているか、それらを導出できるか、などが試されているように思います。第1問の小問をたくさん解き、その中で出てくる公式の意味を理解したり、自身で導出したりすることが、間接的に第2問、第3問の対策になるのではないかと考えました。
本番に向けての学習時間を多く取れるわけでもないことから、選択と集中で第1問の過去問を解くという学習に集中しました。
とにかく過去問が大事
アクチュアリー試験対策はとにかく過去問が大事です。どれだけ確率・統計の勉強をしても方向性の違う勉強では点数が取れません。アクチュアリー試験の直前の11月に統計検定1級の試験が実施されますが、同じ確率・統計の資格試験と言っても問題の性質が全く違います。統計検定1級の勉強をどれだけ頑張ってもアクチュアリー試験で高得点を取るのは難しいのではないかと思います。
私がアクチュアリー試験の対策に過去問が大事だと思う理由は何を覚えないといけなくて、何を覚えなくてよいかがわかることです。
例えば過去問の解答を読むと、以下のようなことが平気で書いてあったりします。
\[
n_1=2(n-t+1),\,\,n_2=2t\\
{n_1}^{\prime}=2(t+1),\,\,{n_2}^{\prime}=2(n-t)\\\\
\frac{n_2}{n_1F_{n_2}^{n_1}(\frac{\epsilon}{2})+n_2}<\hat{p}<\frac{{n_1}^{\prime}F_{{n_2}^{\prime}}^{{n_1}^{\prime}}(\frac{\epsilon}{2})}{{n_1}^{\prime}F_{{n_2}^{\prime}}^{{n_1}^{\prime}}(\frac{\epsilon}{2})+{n_2}^{\prime}} \]
あるテキストでこの数式を見たときに、「これを覚えていることが前提であるような試験が存在するはずはない」と思ってしまいますが、アクチュアリー試験は覚えていることを前提とするのです!この公式を覚えていないとこの問題は解けません。試験中にこの公式を導出するのは不可能だろうと思います。
一方当然ですが、正規分布の上側5%点の値などは数表として与えられるので、覚える必要はありません。
この話に関連して、私が過去問を解く上で常に参照し、書き込みをしていたのが、【アクチュアリー試験 合格へのストラテジー 数学】です。
このテキストは本当に受験生のバイブルと思います。過去問を研究して書かれており、アクチュアリー数学試験に必要な公式がほぼ全て載っているテキストです。先ほどの複雑な公式も載っています。過去問を解いてどのような公式が必要になるか、どのように使われるかを知り、このテキストで整理していきました。テキストの公式には何年の過去問の何番の問題で使われているかを都度書き込み、不安な公式はテキストから過去問を参照し使い方を叩き込みました。この過去問→テキスト、テキスト→過去問の両方向の学習を繰り返し行いました。
私は幸い普段から数学を教える仕事をしているので過去問にすんなり入っていけましたが、いきなり過去問は解けないという方は、こちらのテキストがおすすめです。
弱点克服 大学生の確率・統計 藤田 岳彦(著) 東京図書
先に紹介した「合格へのストラテジー」を監修されている藤田岳彦先生が書かれた確率、統計の問題集で、アクチュアリー試験を意識して書かれています。こちらのテキストで確率分布、統計の手法、モデリングの問題の解き方などに慣れればスムーズに過去問に移行できるでしょう。
確率分布はしっかり手を動かして頭に叩き込む
アクチュアリー試験には「二項分布」、「ポアソン分布」、「正規分布」、「ベータ分布」、「ガンマ分布」など多種多様な確率分布が登場します。第2問、第3問含めてこれらの分布の意味を正確に理解し、式変形できる能力が必須となります。「合格へのストラテジー」には各分布の確率密度関数、平均、分散等がまとまっていますが、その導出は載っていません。
私は記憶力に自信がありません。前節でも触れましたが、覚えるのではなく何度も解くことで必要な公式を体に叩き込ませています。これらの分布の各種の統計量についても「合格へのストラテジー」を眺めて頭に入れることは困難ですし、試験本番で緊張している中ではスムーズに頭から引き出せない自信があります。
そのため、分布の意味をしっかり理解し、そこから確率密度関数を導出できるように、また、定義に沿って平均、分散、モーメント母関数を自分で導出できるように練習しました。導出に時間がかかると試験では全く使えないため、短時間で導けるよう繰り返しノートに書き殴りました。最初の頃は過去問である分布の平均、分散が必要になった場合に、公式は使わずに、都度自力で導いていました。
しかも、平均、分散の求め方は一通りではありません。例えば二項分布の平均は偏微分を用いて導出する方法がありますし、モーメント母関数を用いた導出法もあります。可能な限り全ての方法で都度公式を導いていました。
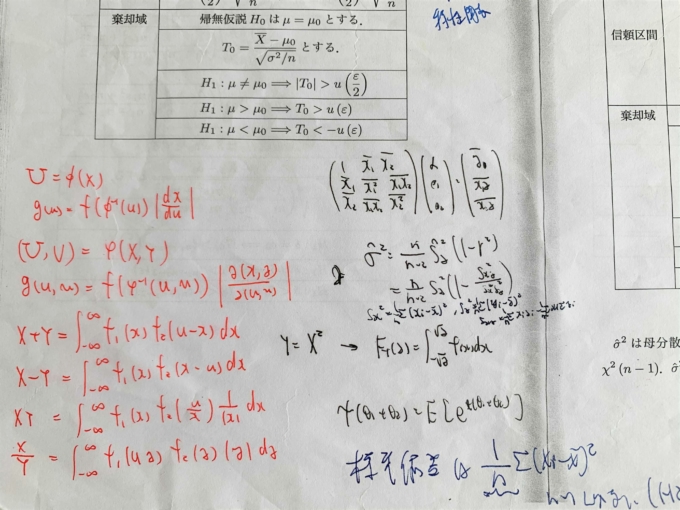
例えば以下は当時、負の二項分布についてまとめたノートです。平均、分散を定義からだけではなく、モーメント母関数を用いて導出していたことがわかります。また負の二項分布の再生性もモーメント母関数を用いて証明しています。

記憶力に自信がないことがこれらのノートを作るモチベーションになり、結果記憶するよりも自信をもって公式を使うことができるようになりました。
確率分布は多種多様ですが、ある分布の特別な場合が他の分布になるということが多々あります。これらをしっかり整理して試験に臨みましょう。
確率分布は平治親分のテキスト
【明解演習 数理統計】の最後に綺麗にまとまっており、こちらも重宝しました。アクチュアリー試験とは記号の定義が違うこともありそこは注意が必要ですが、アクチュアリー試験を受ける方は買っておいて損はないでしょう。(ただし、先述の通り私は過去問こそが大事だと思っているので、平治親分のテキストを全部解けるようになってから過去問をしようとかは考えない方が良いと思います。あくまで辞書的に、また過去問の関連問題を解たいときなどに参照すれば十分ではないかと思います。)
モデリングは捨てない
第1問の小問集は大きく分けると「確率」、「統計」、「モデリング」の3分野から問題が出題されます。モデリングは大学の確率、統計を勉強していても普通は出てこない分野であり、とっつきにくい分野でした。最初は過去問の解答を読んでも意味が全く分からない問題もあったのですが、私の作戦は第1問で満点を取ることだったので、モデリングもしっかり対策しました。
モデリングの各公式は「合格へのストラテジー」にしっかり載っているので、例えばAR(p) 、MA(q)などのモデルの意味をしっかり理解し、公式は自力で導けるよう何度も導出からノートに書きました。
この辺りは確率分布の勉強法と変わらないのですが、敢えて書く理由はそのとっつきにくい性格からモデリングを捨ててしまう方が多くいるからです。
個人の意見ですが、モデリングの問題は簡単です。公式そのままで解ける問題が多く出題されています。私は試験2週間くらい前に過去問からモデリングの問題を集めて一気に対策しました。それで十分間に合いました。時間対効果は一番高い分野と言えますので、捨てずにしっかり対策しましょう。
まとめ
やったことはいろいろありますが、結局アクチュアリーの数学試験は「過去問をやりこむ」に尽きると思います。2018年は不合格でしたが、やはり過去問をあまり解いていなかったことが敗因と思われます。社会人になると学生の頃と比べて試験の数がぐっと減るので、本番では緊張して普段の力が全然出せない方も多いです。私もそうでした。そうならならいためにも過去問を大量に解き、頭は緊張で固まっていても、ある程度は手が勝手に動いて解答を作ってくれるような状態にしていくことが理想です。
私は2019年の本番では第1問の小問12問中正解は8問か9問だったと思います。試験が終わった後に悔しくて泣きたくなるくらいのおっちょこちょいミス、勘違い等が原因ですが、過去問をやりこんでいたおかげで被害を最小限に抑えることができました。足りない分を第2問、第3問から拾いなんとか合格できた形です。
今年もアクチュアリー試験が近づいてきています。私は生保とKKTを受験予定です。アクチュアリー試験を受ける方は一緒に気を引き締めて頑張っていきましょう。
(文/松中)















