リスクとリターンの調整！―ポートフォリオ理論入門その２―

統計・機械学習トピック

公開日

2020年10月16日

更新日

2020年10月16日

こんにちは。和からの数学講師の岡本です。前回に引き続き、株価のリスクやリターンについてお話します。

リスクとリターンの調整！―ポートフォリオ理論入門その１―

前回はうまく株を組み合わせ、うまく投資比率を調整すると、リスクを非常に小さく抑えられるということをお話しました。今回はその「うまい組み合わせ」と、数学的な背景について解説をしていきます。

この記事の主な内容

１．復習

前回扱った株価Aと株価Bについて簡単にまとめます。２つの株価の平均値（リターン）と標準偏差（リスク）は以下のようになっています。

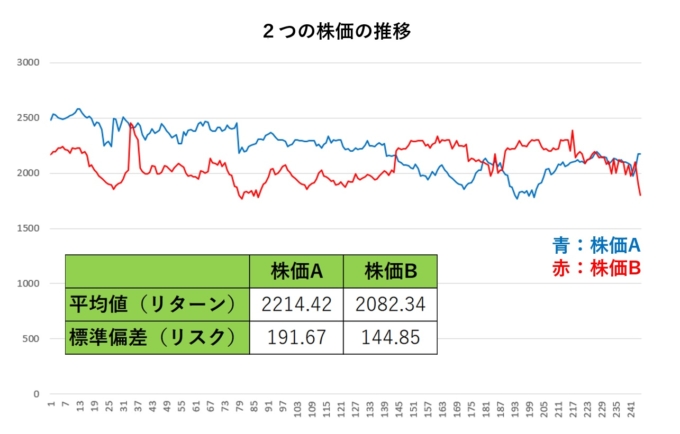
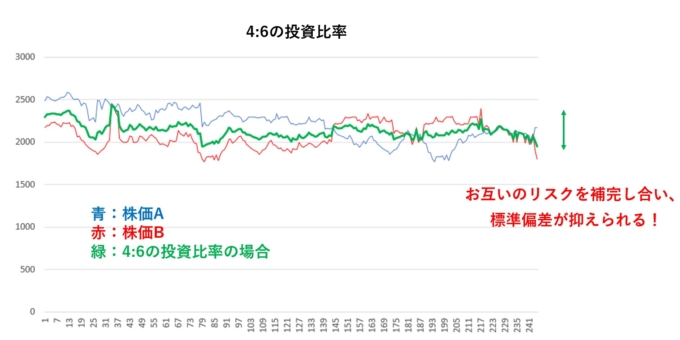
この２つの株をそのまま１：１で投資するのではなく、一定比率（投資比率）を決め、それぞれの株を投資することを考えます。例えば、株価Aを40%、株価Bを60%で設定することで、リスクとリターンが以下のようになるということを前回お話しました。

ご覧のように圧倒的にリスクが小さくなります。今日はこのリターンとリスクの計算の仕組みをお話します。実は、この比率がリスクを最小にすることも数学を使うこと理解できるのです！

２．数学的な説明

まず注意していただきたいのは、前節のような「リスクの大幅削減」はどんな２つの株価に対してもできることではありません。今回扱った株価Aと株価Bはいわば「うまい組み合わせ」なのです。どのような組み合わせがいいのか、順を追って説明しましょう。
まず、株価Aの平均値を\(\mu_A\)、標準偏差を\(s_{A}\)。同じく株価Bの平均、標準偏差をそれぞれ\(\mu_B, s_B\)とします。また株価A、株価Bの投資比率をそれぞれ\(r_A, r_B\)とし、この比率で求められる株価の平均（リターン）を\(M_{r_A,r_B}\)、標準偏差（リスク）を\(S_{r_A,r_B}\)とします。このとき、リターン\(M_{r_A,r_B}\)は

\begin{align*}M_{r_A,r_B}=r_A\cdot \mu_A+r_B\cdot \mu_B\end{align*}

となります。また、株価AとBのデータの関係性を表す「相関係数」を\(\rho_{A,B}\)としたとき、投資比率\(r_A, r_B\)の株価のリスク\(S_{r_A,r_B}\)は以下のような式で与えられます。

\begin{align*}S_{r_A,r_B}=\sqrt{r_A^2s_A^2+r_B^2s_B^2+2r_Ar_Bs_As_B\rho_{A,B}}\end{align*}

つまり、株価AとBの相関係数によって\(S_{r_A,r_B}\)の値が決まります。そもそも相関係数とは、-1から1までの値をとる指標で、1に近いほど「正の相関（win-winの関係）」、-1に近いほど「負の相関（win-loseの関係）」となります。

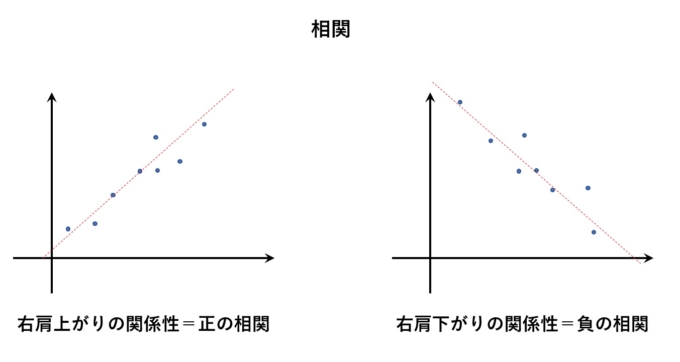
前節のように株価をある比率で合算した場合のリスクを小さくするには相関係数がマイナスの値である（＝AとBが負の相関関係にある）ことが必要不可欠です。実際前節のAとBの相関係数は-0.433であり、\(S_{r_A,r_B}\)のルートの中の値を小さくします。

３．つまり、どんな株の組み合わせがいいのか

数式の説明を踏まえると、負の相関関係にある株価を選べばいいということです。つまり、「１つの株価が下がるとき、もう片方の株価が上がる」といった関係です。こう考えると、「負の相関関係である株価」は、「お互いに助け合い、リスクを軽減している」というイメージもつかめます。

４．ポートフォリオ曲線

では、負の相関関係であるような株価を選んだとして、どの比率が「ベスト」なのかを考えましょう。この「ベスト」な比率を見つける方法としてポートフォリオ理論というものがあります。片方の株価の比率を媒介変数と考え、縦軸をリスク、横軸をリターンとして、平面上にプロットします。たとえば例で扱った株価Aと株価Bについて考えてみます。

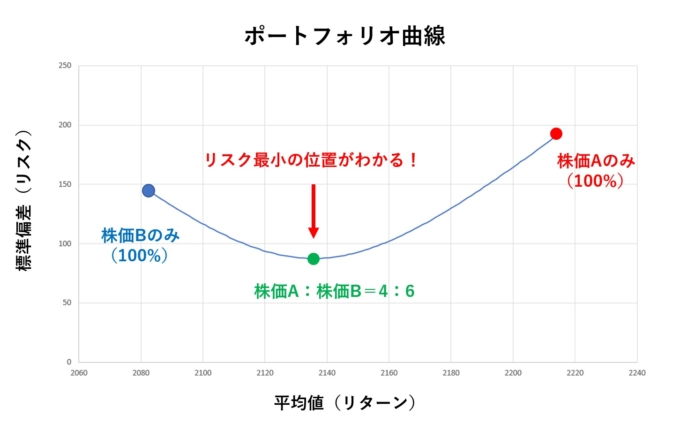
このような曲線のことをポートフォリオ曲線といいます。図をみてみるとリスクが最小になっているところがあります。ここを読み取ると株価Aの比率が40%だということがわかります。つまり、株価Aと株価Bの比率を4:6にしたとき、リスクは最小化されることがわかりました！このようにリスクとリターンの曲線（ポートフォリオ曲線）を描き、最適な比率を考えることができるのです！

５．さいごに

いかがでしたでしょうか。今回は株価の投資比率を調整することでリスクを抑えられることの数学的な説明を行ってきました。構造がわかると理解や応用にもつながります！なにより、具体的にどれだけリスクが下げられるか実際に計算できると楽しいですね！ちなみに今回の内容の参考書籍として、「経済・経営を学ぶための数学入門(ミネルヴァ書房)」がおすすめです。