意外と知らない平行曲線のお話
公開日
2021年2月26日
更新日
2021年2月26日

こんにちは。和からの数学講師の岡本です。今回は「平行な曲線」について簡単に紹介していこうと思います。“平行な曲線”と聞くと、大して複雑そうに聞こえませんが、実は意外にも奥が深いんです。
この記事の主な内容
1.平行な線と平行な曲線
平行な線というと下の図のようにずーっと交わることのない直線のイメージです(平行線が交わる幾何学というのもあるので、今回はそっちには踏み込まない普通の平行線を考えます)。

では“平行な曲線”というものを考えてみましょう。わかり易い例は円です。
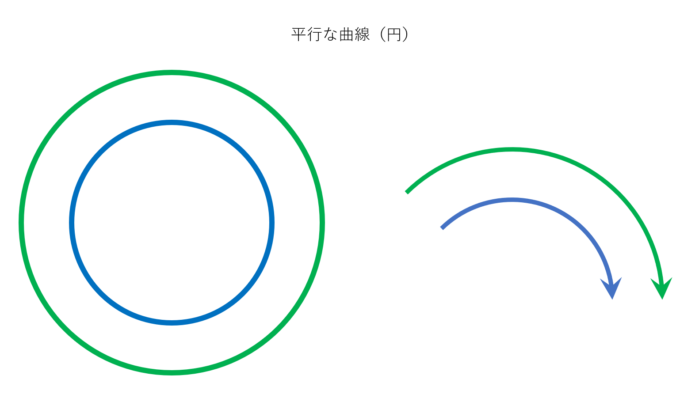
上の図のように、与えられた円の平行線は中心を同じ位置にして半径を変えることで平行な円や円弧を実現できます。では、円とは限らない曲線の平行線ってどう考えればいいのでしょうか?そのためには「平行曲線」というものをきちんと定義する必要があり、これは意外にも複雑です。
2.平行曲線を定義する
図のような野良(のら)の曲線に対する「平行な曲線」というのは、以下のような曲線です。

実は、平行な曲線というのは元の曲線の「コピー」ではありません。コピーの場合、図のように少し歪んでしまいます。「平行な曲線」を描くのはそんなに単純ではなさそうです。
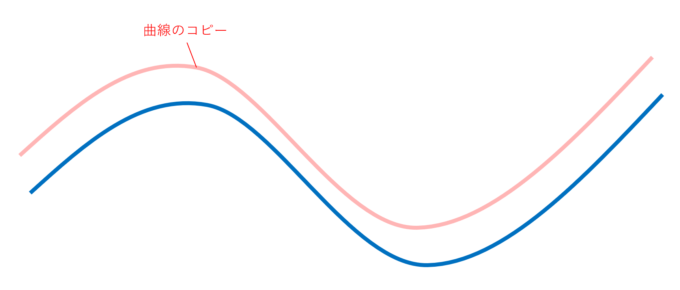
そこで、「平行線」の特徴を思い出しましょう。「平行な線」というのは、垂直な方向に一定距離離れたものです。これを曲線について同じように考えてみます。
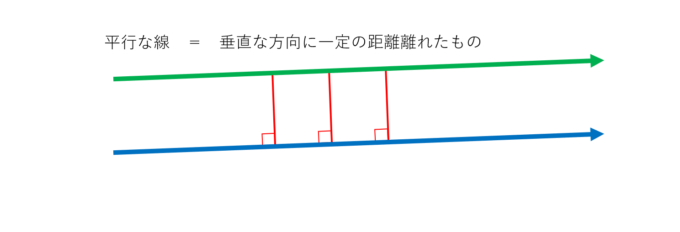
つまり、「平行曲線」とは、各点における進行方向に対して垂直な方向に一定距離離れた曲線と考えます。

こうして、曲線に対しても「平行」を考えることができました!
3.平行曲線の思わぬ落とし穴
具体的な曲線としてコサイン・カーブ\(y=\cos x\)を考えてみましょう。
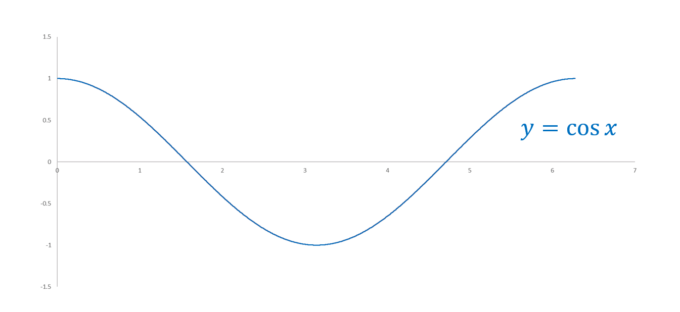
コサイン・カーブの各点における、「進行方向左側に直交する方向」は具体的に計算できるので、一定の距離だけ離れた点の軌跡を求めることができます。下の図は、進行方向左側に、一定の距離\(d=0.5\)離れた平行線をExcelを使って描きました。
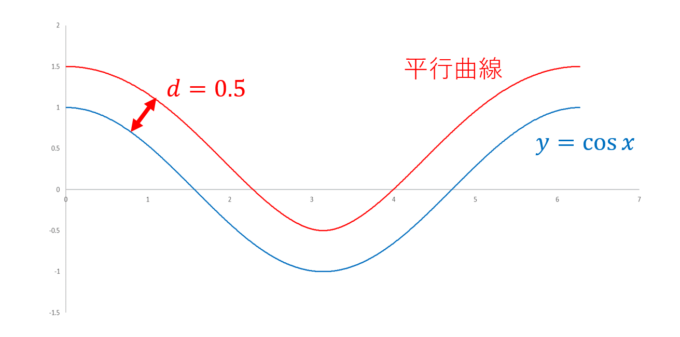
しかし、距離\(d\)を大きくしていくと、「異変」が起こることに気づきます。
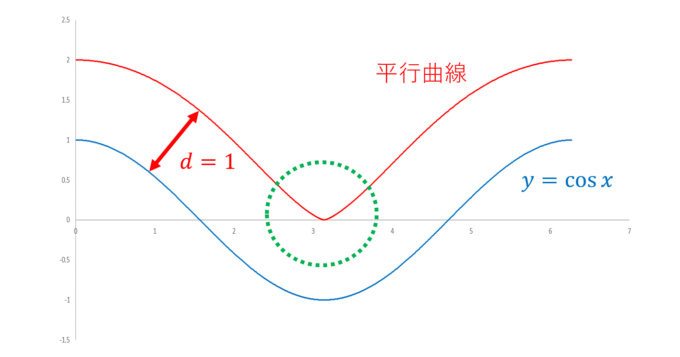
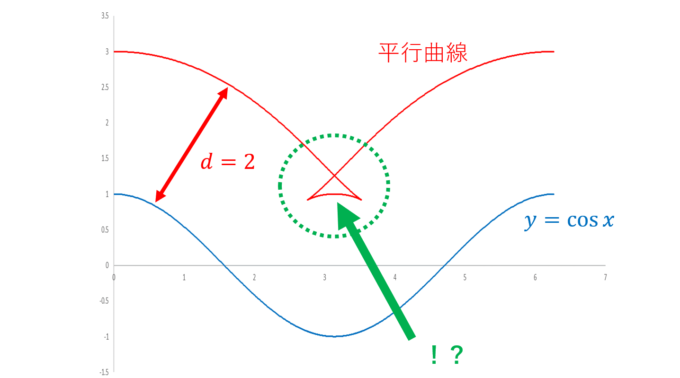
途中か尖った形が現れますね。参考のため、\(d=0.5, 1.0, \ldots 3.0\)までを描いてみました。
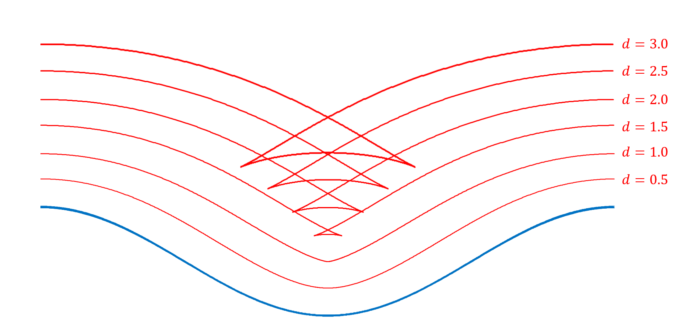
なんだか、ずーっと平和に平行曲線が引けるように思っていましたが、\(d=1\)から事態が急変し、予想外の動きがでてきました。ここまでの考察から、与えられたカーブにおいて、「ある程度距離を取った平行曲線」は尖ってしまう可能性があることがわかりました。逆にある程度距離を取った平行曲線がなめらかになるためには、それなりに曲線自体を大きくし、緩やかなカーブにしなくてはいけません。このような考察は、道路の設計において非常に重要となります。
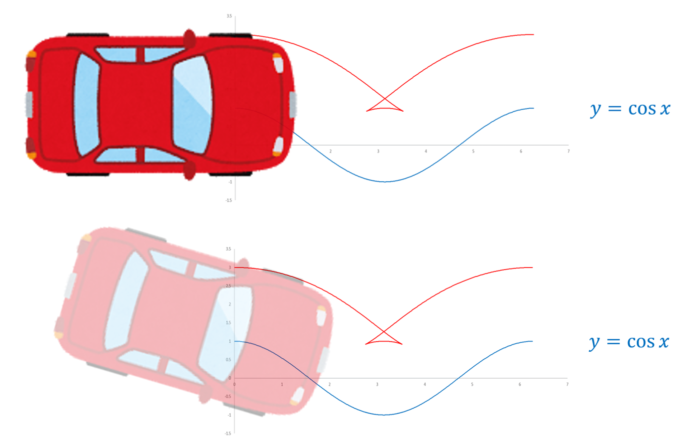
車がカーブに入ってきます。急なカーブでは普通に曲がれないのがわかります。
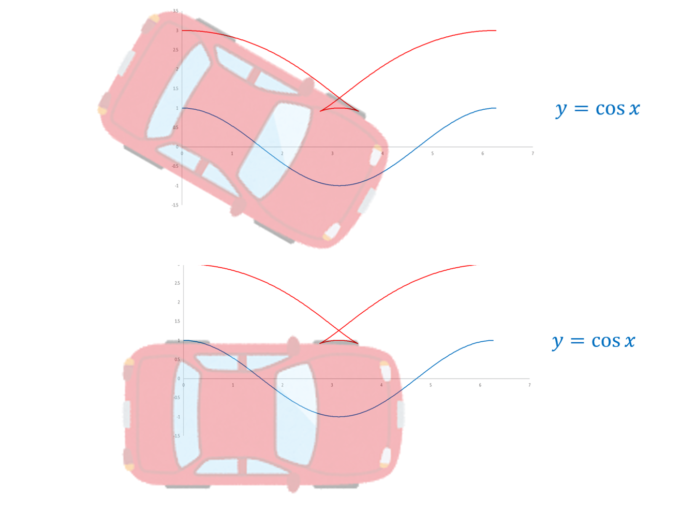
ご覧のように、カーブの先端を通り過ぎた後の左側の車輪は後ろ向きに動きます!
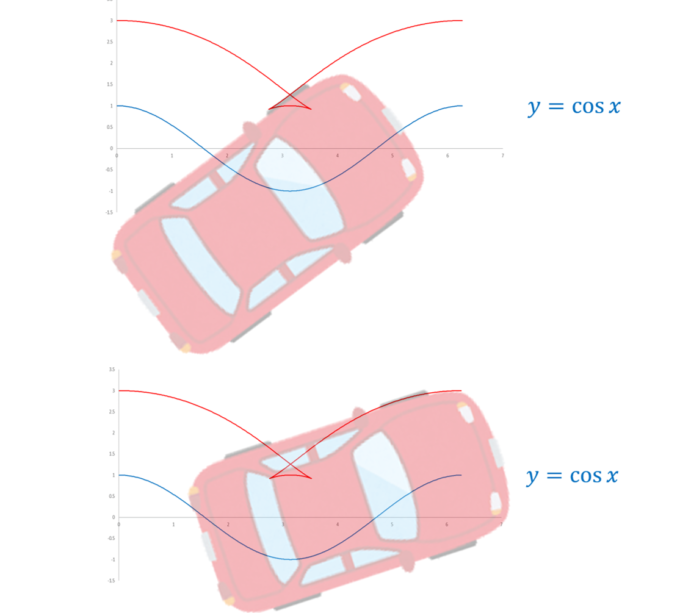
動画でも見てみると左側の車輪が後ろ向きに動いていることがよくわかります。
急なカーブではこのような複雑な動きが要求されます。つまり、スピードがでる高速道路では、車の幅に対してこのような複雑な動きにならないよう十分にカーブを緩やかに設計する必要があります。高速道路の曲線に関しては、クロソイド曲線というものが利用されているお話を以前マスログにまとめました。
実際に高速道路のカーブでは、円弧とクロソイド曲線が多用されます。円弧の平行曲線は先ほど説明した通り、簡単に描けますが、クロソイド曲線の平行曲線はしっかり考えなくてはいけません。意外にも奥が深いですよね!
4.さいごに
さて今回は「平行曲線」という、少しマニアックな幾何学の話題についてまとめてきました。また道路の話題から、日常のあらゆる場面で数学が応用されていることも説明してきました。次回はもう少し数式を使った微分幾何学的な考察を行っていこうと思います。また、今回カーブを描くのに使用したのはExcelです。Excelはうまく活用すれば、いくらでも模様やグラフを描くことができます。Excelを使った図形作成のセミナーとして「Excelアートセミナー」があります。月1回で様々な模様やアートをExcelで描いていくので、興味のある方は是非ご参加ください。
和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>