4で割って1余る素数が2つの平方数で表されることの“一文証明”
公開日
2021年2月24日
更新日
2025年9月17日

こんにちは。和からの数学講師の岡本です。今回は「4で割って1余る素数は2つの平方数の和で表されること」をたった一文で証明する方法について解説していきます。
飲み会や合コンで趣味や興味について聞かれたとき「4で割って1余る素数について考えています」と答えるだけで盛り上がることは間違いないわけですが、それに加えて証明を一文で終わらせることができれば、もう「本日の主役」確定です。
※あくまで岡本個人の意見です。
この記事の主な内容
1.2平方和の定理
この内容については以前マスログで紹介したので、詳しくはこちらをご覧ください
4で割って1余る素数は必ず2つの平方数の和で一意的に表すことができる。
例えば、5, 13, 17, 29, 37は4で割って1余る素数です。これらの素数は
\begin{align*}
5&=1^2+2^2\\
13&=2^2+3^2\\
17&=1^2+4^2\\
29&=2^2+5^2\\
37&=1^2+6^2
\end{align*}
という具合に、確かに2つの平方数の和で表現されています!美しい結果ですよね!これは一般に「2平方和の定理」と呼ばれていますが、1640年12月25日にフェルマーがメルセンヌに対して「2平方の証明ができた!」という内容の手紙を送ったことから、「フェルマーのクリスマス定理」とも呼ばれています。なんだか素敵ですね。ちなみにフェルマーの証明は公開されておらず、最初に証明を与えたのはレオンハルト・オイラーと言われています。オイラーに関する記事も以前マスログで紹介しているので興味のある方は併せてご覧ください。
2.Don Zagierによる一文証明
2平方和の定理は意外にも複雑で、様々な前提知識が必要になります。しかしそんな中、タイトルにあるようにドイツの天才数学者ドン・ベルナルト・ザギエによって「一文証明」が与えられました。一文です!一文で証明が完結するという恐ろしい技を繰り出したのです!では、その証明をご覧ください。
\begin{align*}
(x, y, z)\mapsto
\begin{cases}
(x+2z, z, y-x-z)\cdots x \text{<} y-z\\
(2y-x, y, x-y+z)\cdots y-z \text{<}x \text{<}2y\\
(x-2y, x-y+z, y)\cdots 2y \text{<}x
\end{cases}
\end{align*}
は1つの不動点を持っているので、集合\(S\)の要素数は奇数であり、簡単な対合写像
\begin{align*}
(x, y, z)\mapsto (x, z, y)
\end{align*}
もただ1つの不動点を持つ。【証明終了】
!? となりますよね。私も初めてこの証明を見たとき、何が起こったのか全然わかりませんでした。まさにバトル漫画でよくある「お前はもう、死んでいる」状態です。この証明はこちらから閲覧できます。
https://people.mpim-bonn.mpg.de/zagier/files/doi/10.2307/2323918/fulltext.pdf
次の節ではこの証明の簡単な解説をしていきます。
3.一文証明の解説~何が起こったのか~
まず言葉の説明です。対合写像(involution map)とは2回同じ操作を行うともとに戻る操作のことです。例えば、証明の最後にあるものが簡単な例で、\((x, y, z)\mapsto (x, z, y)\)という操作は、要は「2番目と3番目を入れ替える」という操作になります。そのため、2回入れ替えるともちろんですが、元に戻ります。このような操作を対合写像といいます。では具体例を使いながら解説に入りましょう。いま、\(p\)を4で割って1余る素数であるとします。もし\(p\)が2つの平方数で書けるのだとすると、それは(奇数の2乗)+(偶数の2乗)の形に限ります(偶数同士、奇数同士だと明らかに\(p\)が偶数になってしまうため)。そのため、
\begin{align*}
p=x^2+(2y)^2=x^2+4y^2
\end{align*}
という形になります。しかし、このような\(x, y\)が都合よく存在している保証はありません。そこで、条件を緩めて、
\begin{align*}
p=x^2+4yz
\end{align*}
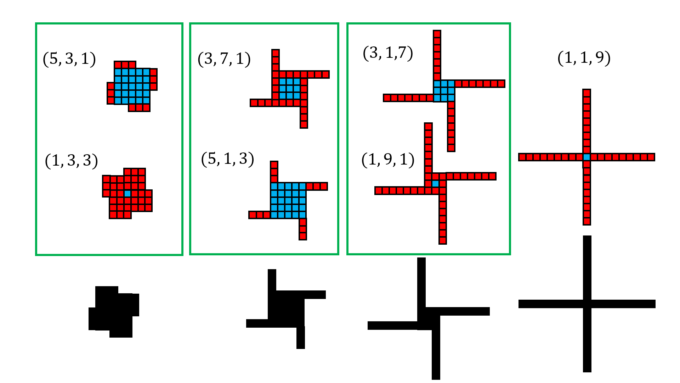
という形の自然数3つ組\(x, y, z\)を考えます。\(p\)は4で割って1余る素数なので、必ず\(p=4k+1\)と表せます。つまり、\(x=1, y=1, z=k\)という3つ組が少なくとも存在します。これにより、証明の最初に定義した有限集合\(S\)は空集合ではないことがわかります。続いて、一見複雑そうに見える1つ目の対合写像ですが、これにはWindmill(風車)を使った明快な幾何学的解釈が知られています。たとえば、\(p=37\)について集合\(S\)を考えてみましょう。
\begin{align*}
37&=5^2+4\cdot 3\cdot 1\Longleftrightarrow (x, y, z)=(5,3,1)\\
&=5^2+4\cdot 1\cdot 3\Longleftrightarrow (x, y, z)=(5,1,3)\\
&=3^2+4\cdot7\cdot 1\Longleftrightarrow (x, y, z)=(3,7,1)\\
&=3^2+4\cdot 1\cdot 7\Longleftrightarrow (x, y, z)=(3,1,7)\\
&=1^2+4\cdot 9\cdot 1\Longleftrightarrow (x, y, z)=(1,9,1)\\
&=1^2+4\cdot 1\cdot 9\Longleftrightarrow (x, y, z)=(1,1,9)\\
&=1^2+4\cdot 3\cdot 3\Longleftrightarrow (x, y, z)=(1,3,3)
\end{align*}
となり、\(S\)の要素は全部で7個となりました。\(p=x^2+4yz\)を満たす3つ組を、\(x\times x\)の正方形と\(y\times z\)の長方形4つを使って以下のように対応させます。
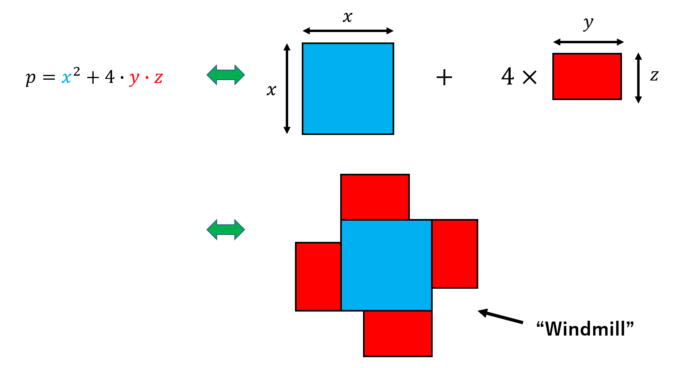
例えば\((5,1,3)\)は以下のような風車型の図形(“Windmill”)に対応します。
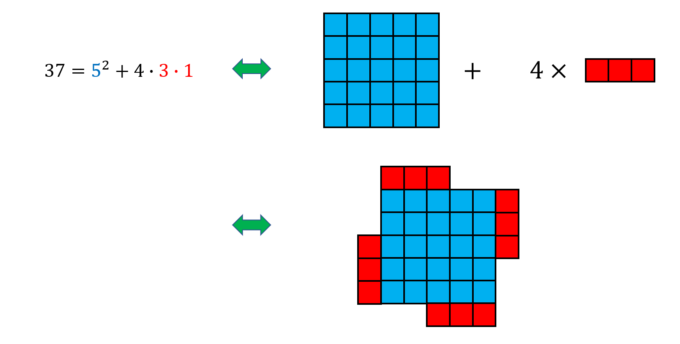
この要領で、7個の要素を風車で表すと次のようになります。
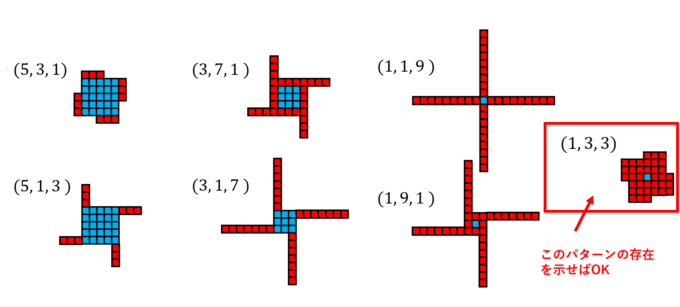
上図右端のような、正方形だけでできる(\(y=z\)となる)パターンの存在が示されれば、証明終了です。では、次に対合写像の意味を考えます。簡単な2つ目の対合写像は\(y\)と\(z\)をひっくり返す対応なので、風車で考えると以下のように長方形を縦でみるか横でみるかの対応になっています。
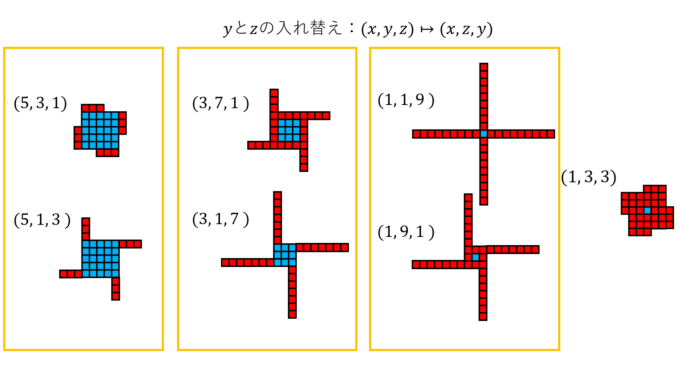
対合写像で移り合うペアは「うまくペアができる」か「1つあまる(不動点)」という2つのパターンになります。「1つあまる」パターンの存在を示すには、\(S\)の要素数が奇数であればいいわけです。それを保証するのが1つ目の対合写像の考察です。この一見複雑そうに見える写像は、実は風車のシルエットが同じになるもの同士を対応させているだけなのです(ただし、風車は逆向きでもOK)。
そして、この「シルエット対応」で変わらない風車は以下のような\((x, x, z)\)のタイプになります。
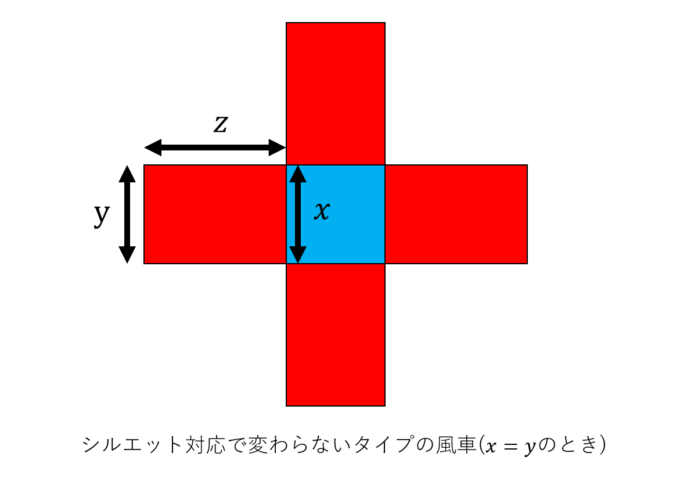
しかし、\(x=y\)の場合、\(p=x^2+4xz=x(x+4z)\)となり、\(p\)が素数だという条件から、\(x=1\)しかありません。これがシルエット対応のただ1つの不動点です。さらに、\(p\)は4で割って1余る素数であるため、\(p=4k+1\)とかけるとします。このとき、不動点は具体的に\((1,1,k)\)と定まります。これにより、「ペア」と不動点1つという構造から\(S\)の要素数が奇数であることが確定しました。こうして、2つ目の対合写像による不動点は図の赤色の部分が長方形でなく、正方形の形をしたもの(\(y=z\))に対応し、見事\(p=x^2+4y^2=x^2+(2y)^2\)となる\(x,y\)の存在が保証できたのです!いや~すっきりです!
4.さいごに
いかがでしたでしょうか?今回は4で割って1余る素数は2つの平方数の和で書けることの最高にクールで難解な証明を解説してきました。
数学は一つ一つかみ砕いていくと全て「当たり前」に見えてきます。しかし、一気に当たり前の状態にはいけないので本を読むとそのギャップに苦戦することが多々あります。和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングをご利用ください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>















