プラスチック数と3次方程式

ロマンティック

公開日

2021年11月24日

更新日

2021年11月24日

動画で見たい方はこちら↓↓↓

こんにちは。和からの数学講師の岡本です。前回に引き続き、「プラスチック数」についてもう少し掘り下げていきたいと思います。前回の記事がこちら。

この記事の主な内容

１．プラスチック比とは(復習)

前回は正方形を3つ相似な長方形で分割する方法を考えました。分割の方法は大きく分けて3通りあり、1つ目は「3等分」、2つ目は「1:3/2」の長方形を使う方法、そして3つ目では、プラスチック数 $\rho=1.3247\ldots$ が現れる、というものでした。

今回の記事では、このあたりをもう少し詳しく、数学的に説明していきたいと思います。

２．プラスチック数の登場

先ほどの長方形分割の話ですが、相似な長方形が大中小と3種類使われています。そこで、中サイズの長方形の短辺を1、長辺を $a$ とおきましょう。また、大きいサイズは中サイズの $x$ 倍、小サイズは中サイズの $y$ 倍であるとしましょう。これらの設定を図にまとめてみます。

この設定における $x$ を具体的に求めていきましょう。まず、全体が正方形であることから

$\begin{align*} ax=x+1. \end{align*}$

また、敷き詰められていることから

$\begin{align*} a+y=ax, ay=1 \end{align*}$

が成り立ちます。これら3つ式を使ってうまく $x$ のみの式にすると、最終的に以下のような3次方程式が得られます。

$\begin{align*} x^3=x+1. \end{align*}$

何を隠そう、この方程式の実数解こそがプラスチック数 $\rho$ なのです！

３．３次方程式を解こう

2次方程式なら中学や高校で習う「解の公式」ですぐに求められますが、3次方程式は難しそうです。しかし、高校までで習いはしませんが、3次方程式にも「解の公式」が存在します。この話だけで記事は2つぐらいかけそうなので、今日はあまり深入りはせずにサクッと解いてみましょう。まず、解きたい方程式は

$\begin{align*} x^3-x-1=0 \end{align*}$

です。次に $x=u+v$ とおくと

$\begin{align*} (u+v)^3-(u+v)-1=u^3+v^3-1+(3uv-1)(u+v)=0 \end{align*}$

となりますが、もし条件

$\begin{align*} u^3+v^3-1=0\\ 3uv-1=0 \end{align*}$

を満たす $u,v$ が求められれば $u+v$ は考えている方程式の解になります（また、 $y=x^3-x-1$ の関数の形を考えると実数解をただ1つ持つことがわかるので1つでも条件を満たす $u, v$ が求められれば $u+v$ が求める実数解になります）。そしてこの条件は

$\begin{align*} u^3+v^3=1\\ u^3v^3=\frac{1}{27} \end{align*}$

と書き換えられるので、 $u^3, v^3$ は2次方程式 $X^2-X+1/27=0$ の解となります。これは2次方程式の解の公式により

$\begin{align*} X=\frac{1\pm \sqrt{1-4/27}}{2}=\frac{1\pm \sqrt{23/27}}{2}=\frac{9\pm \sqrt{69}}{18}. \end{align*}$

したがって、求める実数解 $x$ は上の2次方程式の解それぞれの3乗根を使って

$\begin{align*} x=\sqrt[3]{\frac{9+\sqrt{69}}{18}}+\sqrt[3]{\frac{9-\sqrt{69}}{18}}=1.324717957\ldots \end{align*}$

と表せます（このような解法を「カルダノの解法（公式）」といいます）。実はこの値こそ、プラスチック数なのです！このように、3次方程式 $x^3-x-1=0$ の実数解としてプラスチック数を特徴付けることができました。これはちょうど黄金比が $x^2-x-1=0$ という2次方程式に対応しているのと似ています。

４．値を使って正方形を分割してみよう

ここまでの計算で $x=\rho$ （プラスチック数）であり、 $\rho^3=\rho+1$ を満たすことがわかりました。では、先ほどの設定における、 $a, y$ を求めてみましょう。まず $a$ は

$\begin{align*} a=\frac{x+1}{x}=\frac{\rho^3}{\rho}=\rho^2 \end{align*}$

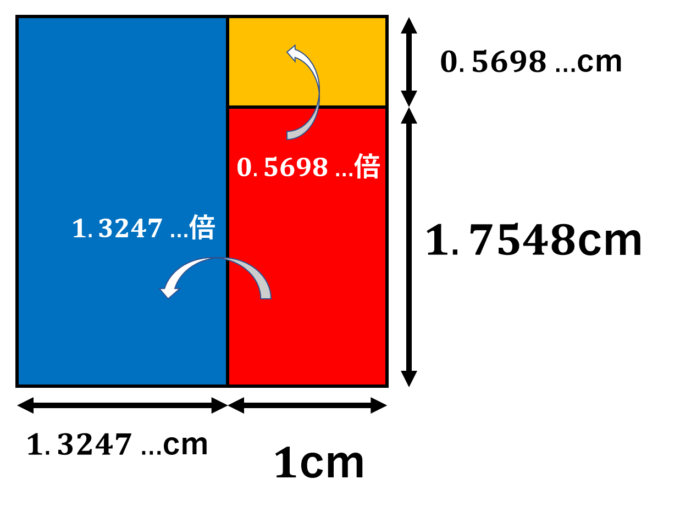
であり、 $a=\rho^2$ であることがわかります、また、 $y=1/x=\rho^{-2}$ であることもすぐにわかります。 $\rho^2=1.7548\ldots$ 、 $\rho^{-2}=0.5698\ldots$ であることから、1cm×1.7548cmの長方形と、約1.3247倍（ $\rho$ 倍）した大きな長方形と約0.5698倍（ $\rho^{-2}$ 倍）した小さな長方形を組み合わせるとうまく正方形を3分割できます。