こんにちは。和からの数学講師の岡本です。今回は「数学セミナー10月号（日本評論社）」の表紙に採用されている切り絵作品について簡単に解説していきます！

数学セミナー2021年10月号 日本評論社

１．シェルピンスキー・カーペット

今回モチーフにしたのは「シェルピンスキー・カーペット」というフラクタル図形です。フラクタル図形に関しては以前マスログで取り上げたので、こちらも併せてご覧ください。

木陰とフラクタル

シェルピンスキー・カーペットとは、以下のように「正方形を9等分割し、真ん中を取り除く」という作業を無限に繰り返すことによってできる複雑な図形です。

もちろん、無限に繰り返したものを描くことはできないので、ある程度のところまでで描写は止めておきます。今回の切り絵はこの図形を利用したデザインになります。

２．多重切り絵だからこそできる表現

シェルピンスキー・カーペットを用いた以下のデザインを3種類用意します。この3つの模様は中心をあわせるように重ねると、図のように大きな隙間がなくなります。

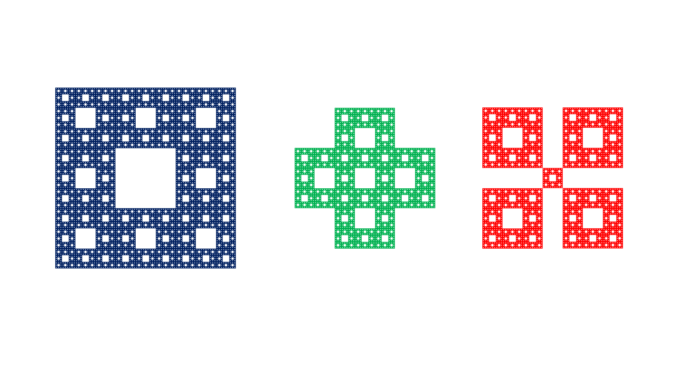
シェルピンスキー・カーペットは最初に除いた正方形などで余白が大きいので、この余白の部分を埋めるために、コピーしたシェルピンスキー・カーペットをずらしてみたのが、このアイデアのきっかけです。

そこで先ほどの3種類のパーツを考え、複数のアクリル板を使う「多重切り絵」として実現させました。

３．ところで何個四角形を切ったの？

よく、「結局何個の正方形を切り取ったのか？」という質問をいただきます。今回は比較的数えやすかったので、自分が大小合わせて何個の穴をあけたのか計算してみることにしました。
そこでまずはシェルピンスキー・カーペットの穴の数について考察します。第\(n\)世代の穴の個数を\(a_n\)としましょう。つまり\(a_1=1\)です。すると次の第\(n+1\)世代では\(a_n\)個の穴を持つ部分が8個になり、真ん中に大きな穴が１つできます。

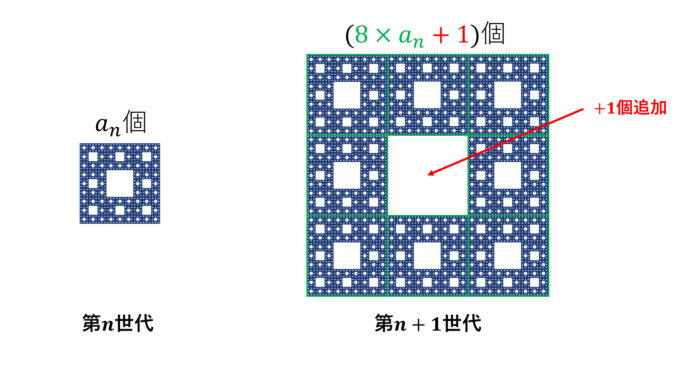
つまり漸化式

\begin{align*}
a_{n+1}=8a_n+1
\end{align*}

が成り立つので、一般項は

\begin{align*}
a_n=1+8^1+8^2+\cdots+8^{n-1}=\frac{8^n-1}{7}
\end{align*}

であることがわかります。これにより、各パーツの穴の数は以下のように計算できます。

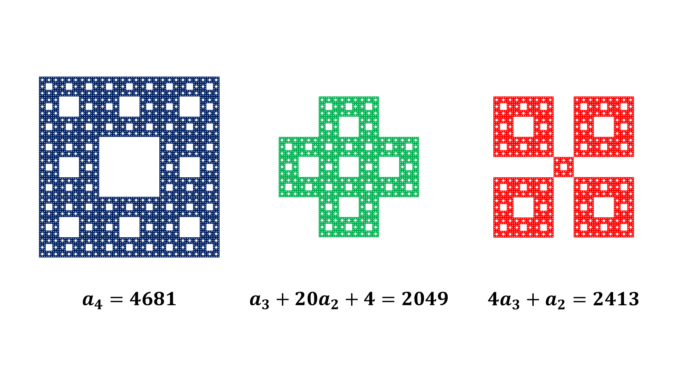
よって切り抜いた穴（正方形）の合計は\(4681+2048+2413=9143\)個であることがわかりました！！1万個近く切っていたのかと思うと自分でもゾっとしますね…。

４．さいごに

いかがでしたでしょうか？数学的なデザインの切り絵は出来上がった後の美しさや達成感が異常に高いので、「次も作ってみよう」という気になります（俗にいう「中毒性」というやつかもしれません）。ちなみに今回ご紹介したシェルピンスキー・カーペットはExcelを使って超簡単に作成できます。工夫すれば様々な模様作成できて楽しいです！

和からでは、数学的なアートやデザインのセミナーをやっています。興味のある方は是非無料のセミナーへお越しください！

Excelアート超入門

数学的デザイン超入門

また、数学アートに関するサブスクリプションサービスも開始しました！無料会員登録もありますので、こちらも併せてご覧ください！

数学アートサロン“MAS”

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>