4月は歴史に残る数学者たち、レオンハルト・オイラー、カール・フリードリヒ・ガウスの誕生月として特定の界隈で知られていますが(笑)、実は日本でも歴代最高の数学者のひとり、広中平祐教授の誕生月でもあります！

「数学のノーベル賞」ともいわれるフィールズ賞を受賞した歴代2人目の日本人であり、1975年には科学技術や芸術などの文化の発展や向上にめざましい功績を挙げた者に授与される、文化勲章を受章しました。さらに日本の算数・数学教育にも多大な貢献をしてくださっており、数理科学振興会（現代表理事、2021年4月時点）を創設して数学研究を後押ししている他、算数オリンピック（現会長）を立ち上げたことでも知られている、日本の数学界のスター的存在です。

今回は、そんな広中先生について見ていきましょう。

広中平祐先生ってどんな人？

広中先生は1931年に山口県由宇町で生まれ、15人兄弟の7番目として生まれました。父は大手の呉服商や織物工場を営んでおり、地域でも有数の裕福な家庭に生まれました。しかし戦争がはじまり敗戦していく中で会社は没落し土地や財産も失い、一転して貧しい生活を強いられます。

日本全体も敗戦ムード漂う中、湯川秀樹教授が日本人初のノーベル賞を受賞した時に国中が沸き立ち、彼に憧れて京都大学入学当初は物理学の道に進みます。しかし大学の講義を受ける中でアインシュタインの相対性理論や連続群と呼ばれる数学の概念に興味を持つようになり、やがて数学に転向しました。大学卒業後はハーバード大で博士号を取得し、ブランダイス大を経て33歳でコロンビア大学教授、1968年に38歳の若さでハーバード大学教授となりました。そして1970年、「特異点解消の定理」と呼ばれる定理で39歳のときにフィールズ賞を受賞したのです。

そもそもフィールズ賞って何？

皆さんは数学にはノーベル賞は存在しないことをご存知でしょうか。ノーベル賞は、毎年10月ごろに経済学や医学などの各分野で最も人類に貢献した研究者に対して授与されますが、実は数学という分野がないのです。理由としては賞を設立したダイナマイトの発明で知られるアルフレッド・ノーベルの恋敵が数学者であったから、などと言われることもありますが真意は不明です。

フィールズ賞は1936年から始まり現在83名の受賞者を輩出しており、「数学分野におけるノーベル賞」とも呼ばれています。日本では歴代3名受賞しており、広中先生は日本では歴代2番目として、39歳のときに受賞されました。実はフィールズ賞には受賞の年齢制限があり、40歳を超えた数学者は受賞できないため、かなりギリギリでの受賞だったのです。

広中平祐の行った研究

広中先生がフィールズ賞を受賞した研究は、「標数0の体の上の代数多様体における特異点の解消」と呼ばれる問題に関するものでした。この問題の意図を十分に理解するためは「代数幾何」と呼ばれる分野の知識が必要になるので今回は深入りはしないでおきつつ、問題の中に登場する「特異点」を切り口に、広中先生の功績を考えてみようと思います。

「特異点」とは？

特異点の説明としては、ひとまず「ある一点だけ滑らかでない部分」と考えるといいでしょう。例えば、遊園地にあるジェットコースターは基本的に特異点、つまり「滑らかでない部分」というのは存在しません。急降下するコースターも、タイヤがレールからが外れないように必ず滑らかに繋がっています。

一方で、次の図形は原点（x座標, y座標ともに0の場所）に滑らかでない点、すなわち特異点があります。

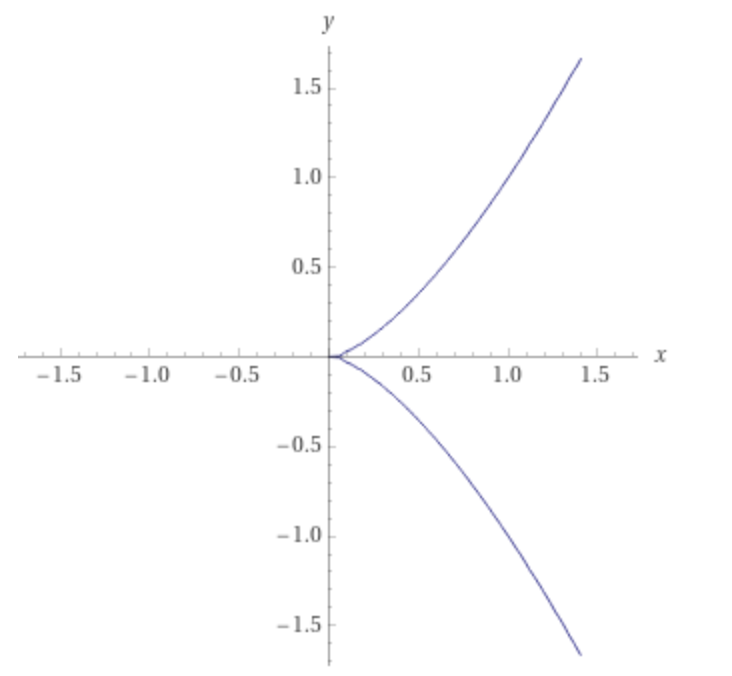
特異点というと、皆さんは去年のノーベル物理学賞の内容を覚えているでしょうか。物理学者ロジャー・ペンローズによって、ブラックホールは数学のある方程式から理論的に導かれることが示され、人類の宇宙に対する理解が一新されました。相対性理論と量子力学に基づく計算の結果、実はブラックホールは方程式における特異点であることがわかったのです！

ブラックホールと特異点の関係性については過去記事でも取り上げていますので、よろしければ合わせてご覧ください。

アインシュタイン以来の天才！？ノーベル物理学賞受賞ロジャー・ペンローズが生み出した現代宇宙観

そんな特異点ですが、図形や方程式を扱う上で非常に重要であると同時に、実用的には「はなはだ不都合で、やっかいな」ものだったのです。特異点をなくすためにはどうすれば良いのか、それが広中先生を含む当時の数学者が活発に研究を行っていた「特異点の解消」なのです。個別的なケースについては当時から様々に計算が行われていましたが、広中先生は特異点を解きほぐして滑らかにする「特異点解消の定理」を導きました。1963年にアメリカの論文誌「Annals of Mathematics」に掲載され、20世紀に生まれた非常に重要な定理の一つとして、世界中にその功績が認められています。

終わりに

ここまで広中先生が研究してきた「特異点の解消」とは何かを見てきましたが、いかがでしたでしょうか。図形の「特異点」と「方程式」の関係を調べる「代数幾何」ですが、実は高校でも入り口として、「図形」と「方程式」の関係を学んでいます。興味が湧いた方は、高校生の時に学んだ内容を見直してみると、当時と違った視点で楽しめるかもしれません。

和からでは数学の様々な分野について1人1人の学びたい内容に合わせた授業を展開しています。「数学が分かるようになりたい！」「学生のころ勉強したあの数学の意味は？」「数学って何の役に立っているの？」など数学について知りたい、分かりたいと思った方はいつでも和からへお越しください。

図形と方程式

「広中先生についてもっと知りたい！」と思った方は、下記の書籍がおすすめです。

学問の発見 数学者が語る「考えること・学ぶこと」 広中 平祐 (著) 講談社

それではまた。

<文/岡崎 凌>
⇒ 講師紹介ページへ