みなさんこんにちは！和からの数学講師の岡本です。今回は前回に引き続きの「三角比」や図形に関する入試問題を解いていきたいと思います。

１．1991年北海道大学

図形問題はとりあえず下手でもいいので絵を描くことがポイントです。まず$\angle A=120°$を意識した三角形$ABC$を描いてみます。次に二等分線を引いて、$BC$との交点$D$を描きます。

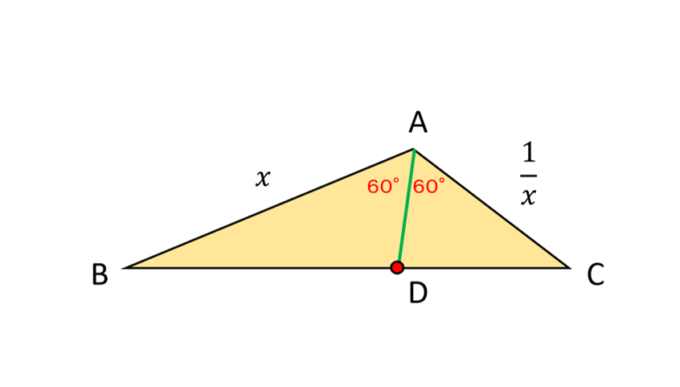
(1)から考えましょう。$AB=x$とすると、$AB\cdot AC=1$であることから$AC=\frac{1}{x}$となります。そして、求めたいのは$AD$の長さですので、これを$y$と置いておきましょう。いろんな求め方があるかもしれませんが、せっかく、120°や二等分にした60°の情報もあるので、「三角形の面積」に注目していくことにします。図より、三角形$ABC$の面積は三角形$ABD$と三角形$ACD$の面積の合計に等しいことがわかります。また、三角形の面積は2つの辺の長さとその間の角度の「サイン」を使うことで計算することができます。これにより、
$$\begin{align*} &[\text{三角形}ABC\text{の面積}]=\frac{1}{2}AB\cdot AC \sin (120°)=\frac{\sqrt{3}}{4}\\ &[\text{三角形}ABD\text{の面積}]=\frac{1}{2}AB\cdot AD \sin (60°)=\frac{xy\sqrt{3}}{4}\\ &[\text{三角形}ACD\text{の面積}]=\frac{1}{2}AD\cdot AC \sin (60°)=\frac{y\sqrt{3}}{4x} \end{align*}$$
したがって、
$$\begin{align*} \frac{xy\sqrt{3}}{4}+\frac{y\sqrt{3}}{4x}=\frac{\sqrt{3}}{4}\Leftrightarrow xy+\frac{y}{x}=1\Leftrightarrow y=\frac{x}{x^2+1} \end{align*}$$
であることが求まりました。
(2)に関してですが、(1)で求めた$AD$は$x$の値によって変化するので、$x$の関数と考えることができます。関数の最大値などを求めるときは、通常微分を行ったりするものですが、今回はそこまでしなくてもよさそうです。というのも、$AD$の式は
$$\begin{align*} AD=\frac{1}{x+\frac{1}{x}} \end{align*}$$
であり、分母の$x+\frac{1}{x}$が最小値をとるとき、$AD$は最大になります。なお、$x+\frac{1}{x}$のようなタイプの最小値を求める問題は頻出で、「相加相乗平均の不等式」を利用します。
これにより
$$\begin{align*} x+\frac{1}{x}\geq 2\sqrt{x\cdot\frac{1}{x}}=2 \end{align*}$$
また、等号成立条件は$x=\frac{1}{x}$、つまり$x=1$となります（$x>0$であることから）。したがって、$x=1$のとき、ADは最大値$\frac{1}{2}$となることがわかりました。「三角形の面積の公式」、そして忘れたころに登場する「相加相乗平均の不等式」を等号成立条件まで正しく押さえておきえすれば、たとえ激しい二日酔いの中でも即答できます。

２．2011年京都大学

先ほどの問題と似ています。この問題には様々な解法が考えられますが、なるべくシンプルに考えていこうと思います。まずは図を描いてイメージしましょう。

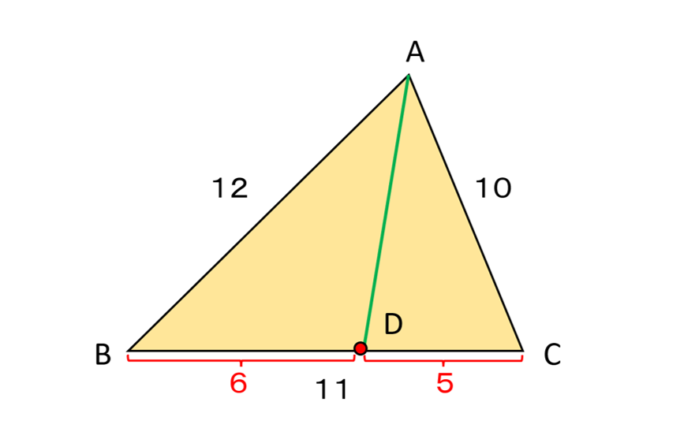
$\angle A$における角の二等分線の性質から、$AB:AC=BD:DC$となることがわかります。なお、$AB:AC=12:10=6:5$であり、$BC=11$であることから、$BD=6, DC=5$であることが明らかになりました。また三角形$ABC$における余弦定理より、$\cos B$を求めることができます。
$$\begin{align*} \cos B=\frac{12^2+11^2-10^2}{2\cdot 12\cdot 11}=\frac{5}{8} \end{align*}$$
$\cos B$の値がわかったので。三角形$ABD$に対して余弦定理を考え、$AD$の長さを求めることができます。
$$\begin{align*} AD^2=12^2+6^2-2\cdot 12\cdot 6\cdot \cos B=90 \end{align*}$$
したがって、$AD=\sqrt{90}=3\sqrt{10}$であることが求まります。余弦定理というのは、三角形に対して「２つの辺とその間の角の$\cos$がわかると、残りの辺の長さがわかる」つまり、「３つの辺の長さがわかると角の$\cos$がわかる」という様々な使い方があるのがポイントです。このように余弦定理を正しく理解していれば、逆立ちしながらでも容易に解くことができると思います。

３．さいごに

いかがでしたでしょうか？大学入試問題は受験では緊張感があってあまり楽しめるのではないかもしれませんが、数学の学び直しや、理解度の確認においては非常に有意義のあるもです。また、問題の背景や題材の元ネタなどがわかると単純に楽しんで取り組むことができます。最近では、脳トレ（脳の活性化のためのトレーニング）や生涯学習の一環として大学入試問題を趣味で解く方もいらっしゃいます。
また、和からでは高校数学の学び直しのための1年カリキュラムがあります！全48回で高校3年間分の数学やその歴史、実社会でどのように数学が活用されいるのかなど、数学の有用性や奥深さ、美しさを「楽しんで」学んでいきます。各回の講座終了後には復習動画が配信されるので、講義を休んでしまっても大丈夫です！なお、途中からの参加も可能です（その場合、終了した講座は動画視聴になります）！
↓詳しくはこちら！

１年で見える世界が変わる！大人のための高校数学講座

なお、高校数学や中学数学の学び直しに関する無料ガイダンス講座も開講いたします！興味のある方はぜひお越しください。

【これが本当の楽しみ方】大人のための数学再学習ガイド-大人だからこそ理解できる数学の面白さ-

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>