みなさんこんにちは！和からの数学講師の岡本です。いままで様々な数学に関する記事を書いてきましたが、今回は大学入試問題を岡本視点で解説し、数学の解き方や面白さを紹介していきたいと思います。

１．2008年慶応義塾大学

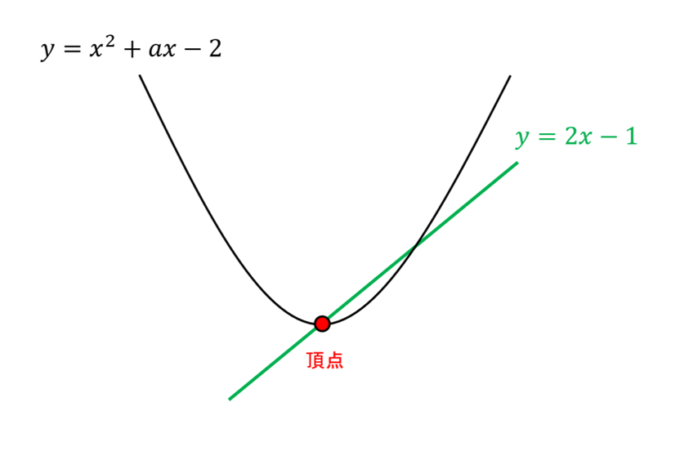
放物線が与えられていますが、\(a\)という文字のため、位置が確定できていません。しかし、放物線の頂点が\(y=2x-1\)上に乗っているというヒントから\(a\)の値が確定できそうです！
まずは放物線（2次関数）の頂点を求めるために、「平方完成」を行いましょう。
\begin{align*}
y=x^2+ax-2=\left(x+\frac{a}{2}\right)^2-\frac{a^2}{4}-2
\end{align*}
したがって、放物線の頂点は\(a\)を用いて\((-\frac{a}{2}, -\frac{a^2}{4}-2)\)と表すことができます。これが\(y=2x-1\)という直線上に乗っていることから、
\begin{align*}
-\frac{a^2}{4}-2=2\times \left(-\frac{a}{2}\right)-1 &\Leftrightarrow a^2-4a+4=0\\
&\Leftrightarrow(a-2)^2=0
\end{align*}
よって、条件を満たすのは\(a=2\)のときであることがわかります！頂点の求め方、直線上にあることの条件式がわかると簡単に解くことができます！

２．2006年滋賀大学

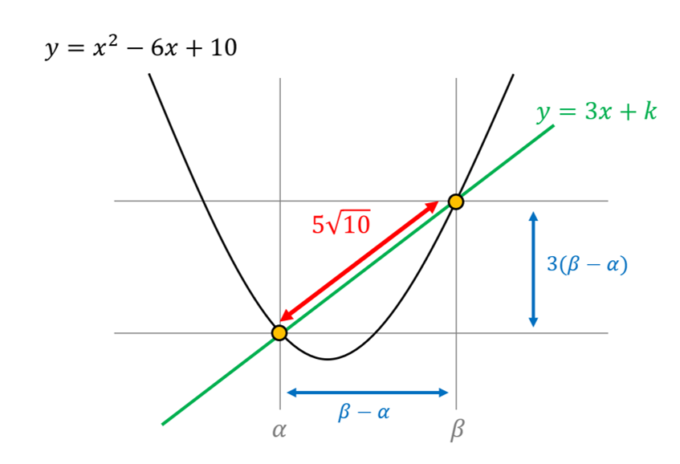
直線と放物線の交点に関する問題です。何も考えず、２つの式をイコールで結んで、交点の\(x\)座標を求めてもいいですが、ここでは悪手です。まずは最終的なヒントである、「PQ間の距離が\(5\sqrt{10}\)である」という条件をわかりやすくするために、ここでは交点P,Qの\(x\)座標をそれぞれ\(\alpha, \beta\)(\(\alpha<\beta\))とおきましょう。このとき、P,Qの\(y\)座標は「\(y=3x+k\)上にある」という条件から\(3\alpha+k, 3\beta+k\)であることがわかります！（注意：PQは放物線上にあることから、\(\alpha^2-6\alpha+10, \beta^2-6\beta+10\)と表すこともできますが、2次の式であるためこの後の計算が煩雑になる可能性があるのでお勧めしません) このとき、PQの距離の2乗は三平方の定理から次のように表すことができます。
\begin{align*}
（PQ）^2 &=(\beta-\alpha)^2+(3\beta+k-3\alpha-k)^2\\
&=(\beta-\alpha)^2+9(\beta-\alpha)^2\\
&=10(\beta-\alpha)^2
\end{align*}
また、条件「PQ間の距離は\(5\sqrt{10}\)」であることから
\begin{align*}
(PQ)^2=10(\beta-\alpha)^2=(5\sqrt{10})^2=250 \Leftrightarrow (\beta-\alpha)^2=25
\end{align*}
したがって、今回の条件は「交点P,Qの\(x\)座標の差の2乗は25である」と言い換えることができました。それでは、実際に交点の\(x\)座標を求めてみましょう。2つの式をイコールで結び、次の2次方程式の解が求める\(x\)座標です。
\begin{align*}
x^2-6x+10=3x+k &\Leftrightarrow x^2-9x+10-k=0\\
&\Leftrightarrow x=\frac{9\pm\sqrt{81-4(10-k)}}{2}
\end{align*}
したがって、\(\beta-\alpha=\sqrt{81-4(10-k)}\)であることがわかります。これにより
\begin{align*}
(\beta-\alpha)^2=81-4(10-k)=25 &\Leftrightarrow 81-40+4k=25\\
&\Leftrightarrow k=-4
\end{align*}
したがって、求める\(k\)の値は4であることがわかりました。
このように、交点の座標や2点間の距離をなるべく簡潔に表現・計算を行うことができればきちんと正解を導くことができるようになります。

３．さいごに

いかがでしたでしょうか？大学入試問題は受験では緊張感があってあまり楽しめるのではないかもしれませんが、数学の学び直しや、理解度の確認においては非常に有意義のあるもです。また、問題の背景や題材の元ネタなどがわかると単純に楽しんで取り組むことができます。最近では、脳トレ（脳の活性化のためのトレーニング）や生涯学習の一環として大学入試問題を趣味で解く方もいらっしゃいます。
また、和からでは高校数学の学び直しのための1年カリキュラムがあります！全48回で高校3年間分の数学やその歴史、実社会でどのように数学が活用されいるのかなど、数学の有用性や奥深さ、美しさを「楽しんで」学んでいきます。各回の講座終了後には復習動画が配信されるので、講義を休んでしまっても大丈夫です！なお、途中からの参加も可能です（その場合、終了した講座は動画視聴になります）！
↓詳しくはこちら！

１年で見える世界が変わる！大人のための高校数学講座

なお、高校数学や中学数学の学び直しに関する無料ガイダンス講座も開講いたします！興味のある方はぜひお越しください。

【これが本当の楽しみ方】大人のための数学再学習ガイド-大人だからこそ理解できる数学の面白さ-

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>