入試問題で数学を楽しもう!~微分編~
公開日
2024年2月16日
更新日
2024年2月16日
みなさんこんにちは!和からの数学講師の岡本です。今回は高校数学の要の1つともいえる「微分」に関連する問題を解いていこうと思います。
この記事の主な内容
1.2006年久留米大学
このような、文字\(k\)によって変わる方程式の実数解の個数を整理する問題はよく目にします。早速解いていきましょう。まずは、\(k\)と\(x\)の式に分離して2つの関数を考えます。つまり、\(y=x^3-2x^2\)という3次関数と\(y=k\)という直線(高さが一定の関数)を考えます。与えられた方程式の実数解の個数は、これらの交点の個数であると考えることができるので、まずは\(y=x^3-2x^2\)のグラフの形を確定させましょう。3次関数\(y=x^3-2x^2\)の概形を考えるために微分を行い、2つの極値の位置を計算します。
\begin{align*}
y’=(x^3-2x^2)’=3x^2-4x=x(3x-4)
\end{align*}
となり、\(y’=0\)となる\(x\)は\(x=0,4/3\)であることがわかります。これをもって、「増減表」を作成します。増減表とは、極値の位置や導関数\(y’\)の符号、それに対応する\(y\)の動きや値をまとめた表です。
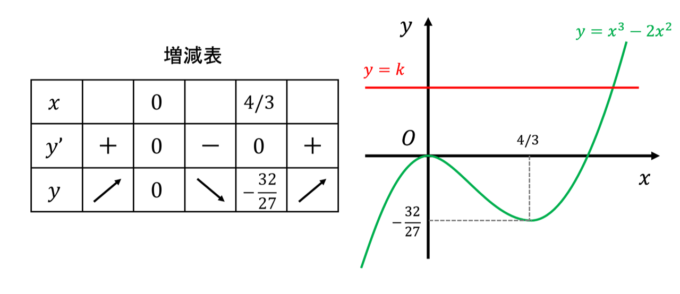
これにより、\(x=0\)で極大値\(0\)、\(x=4/3\)で極小値\(-32/27\)であることがわかります。こうしてグラフの概形を描くことができます。次に、\(y=k\)のグラフですが、これは単純に高さが\(k\)の直線であり、\(k\)の値によって交点の個数はいくつかのパターンに分けられます。
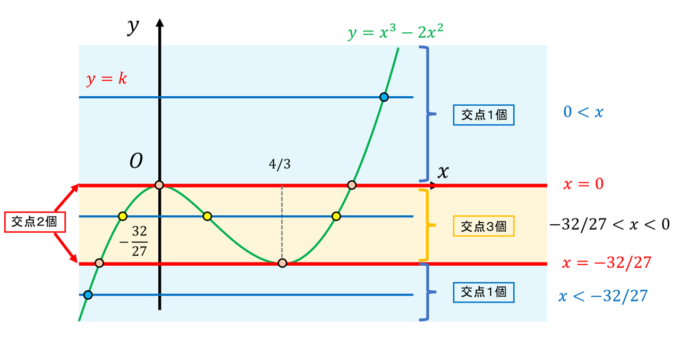
図より、\(k<-32/27, 0<k\)のとき交点は1つ、つまり実数解は1個。また、\(k=0, -32/27\)のとき交点は2つ、つまり実数解は2個となります。最後に\(-32/27<k<0\)のとき、交点は3つであるので、実数解は3個であることがわかります。以上により、求める\(k\)の値の範囲は\(-32/27<k<0\)となります。こちらでコントロールできる\(k\)と、複雑な形になる\(x\)の関数を分離することで、実数解の個数を整頓することができます!
2.1992年学習院大学
\(n\)など、文字がたくさんあって難しそうに見えますが、塊で考えると整理できます。示したい不等式の両辺を\(y^n\)で割ると、
\begin{align*}
\frac{x^n}{y^n}+(n-1)\frac{y^n}{y^n}\geq \frac{nxy^{n-1}}{y^n}\Leftrightarrow \left( \frac{x}{y}\right)^n-n\left(\frac{x}{y}\right)+(n-1)\geq 0
\end{align*}
と整理できます。これにより\(t:=x/y\)とすれば、正の整数\(n\)に対し\(f(t):=t^n-nt+n-1\geq 0\)であることを示せばよさそうです(\(x, y\)は正の実数なので、\(t\)も正の実数全体を動くと想定できます)。まず、\(n=1\)のとき、どんな\(t\)に対しても\(f(t)=0\)となるので、示したい不等式は等号が成り立ちます。次に、\(n>1\)の場合を考えます。関数としての\(f(t)\)の変化を見たいため、微分してグラフの概形を描いてみましょう。\(f'(t)=nt^{n-1}-n=n(t^{n-1}-1)\)であるので、\(f'(t)=0\)となる実数は\(t=1\)のみとなりす(\(t^{n-1}-1=(t-1)(t^{n-2}+t^{n-3}+\cdots+t+1)\)であり、\((t^{n-2}+\cdots+1)>0\)であることから\(t=1\)のみとなります)。したがって、増減表は下記の通りです。
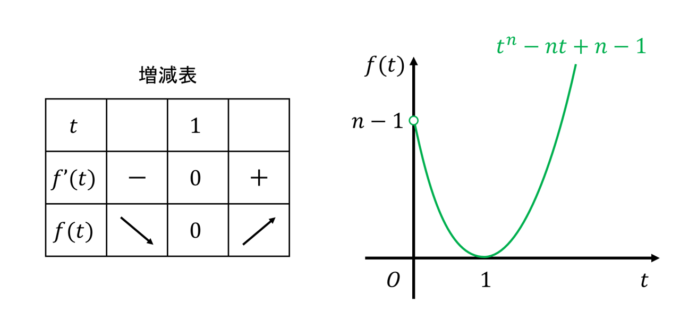
よって、\(t=1\)のときが極小値となり、その値は\(f(1)=0\)であるので、任意の正の実数\(t\)に対して\(f(t)=t^n-nt+n-1\geq 0\)であることがわかりました。これにより、任意の正の実数\(x, y\)、正の整数\(n\)に対して不等式
\begin{align*}
x^n+(n-1)y^n\geq nxy^{n-1}
\end{align*}
が成り立つことが示されます。なお、\(n=1\)または\(t=x/y=1\Leftrightarrow x=y\)のとき、不等式の等号が成り立つこともわかります!このように、微分を使った不等式の証明問題も頻出問題であり、数学検定や大学入試問題でよく取り上げられます。また不等式の問題は別解や背景となる現象があることが多く、単純に面白いです。不等式に興味のある方はこちらのマスログもぜひご覧ください。
3.さいごに
いかがでしたでしょうか?大学入試問題は受験では緊張感があってあまり楽しめるのではないかもしれませんが、数学の学び直しや、理解度の確認においては非常に有意義のあるもです。また、問題の背景や題材の元ネタなどがわかると単純に楽しんで取り組むことができます。最近では、脳トレ(脳の活性化のためのトレーニング)や生涯学習の一環として大学入試問題を趣味で解く方もいらっしゃいます。
また、和からでは高校数学の学び直しのための1年カリキュラムがあります!全48回で高校3年間分の数学やその歴史、実社会でどのように数学が活用されいるのかなど、数学の有用性や奥深さ、美しさを「楽しんで」学んでいきます。各回の講座終了後には復習動画が配信されるので、講義を休んでしまっても大丈夫です!なお、途中からの参加も可能です(その場合、終了した講座は動画視聴になります)!
↓詳しくはこちら!
なお、高校数学や中学数学の学び直しに関する無料ガイダンス講座も開講いたします!興味のある方はぜひお越しください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>













