トポロジー有名定理その3~ボルスク・ウラムの定理~
公開日
2021年10月9日
更新日
2021年10月9日

※本記事はロマ数トレラン「微分トポロジー入門-境界付き多様体とmod 2交差理論-」の講師である佐々木和美先生によるトポロジーの有名定理の解説記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。
この記事の主な内容
1.はじめに
こんにちは。和から講師の佐々木です。ロマ数トレラン「微分トポロジー」に関連して、トポロジー分野で有名な定理を解説していきます。第1回ブラウワーの不動点定理と第2回ジョルダン・ブラウワーの分離定理に引き続き、今回はボルスク・ウラムの定理をご紹介します。
2.パンケーキとハムサンドイッチ
突然ですが、パンケーキとハムサンドイッチでは、どちらがお好きですか?
2枚のパンケーキを1回の(皿に垂直な)カットで同時に2枚とも等分にできる!
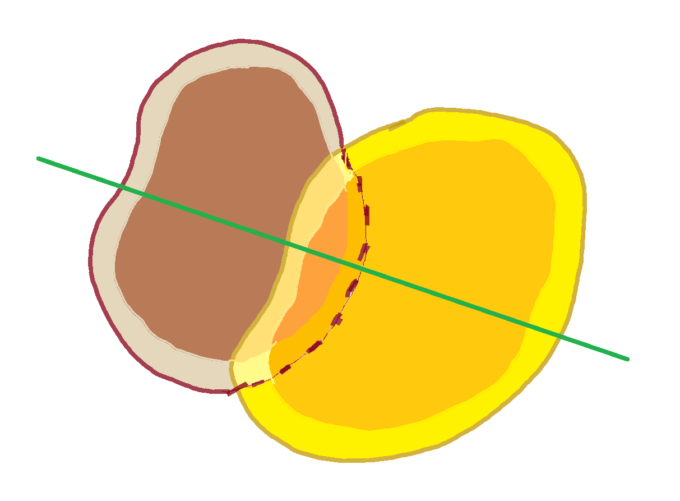
ちなみに、この定理「パンケーキ」が正式名称なのですが、普通のパンケーキ2枚をそれぞれ等分にするというのも変なので、「チョコソース掛けパンケーキの定理(パンケーキ1枚とそれにかけられたチョコソースを1回のカットで同時に等分にできる!)」と呼ぶことを提案します!
具材が3つの場合も、切断面が傾くことを許せば等分にできます。
ハムとチーズとパンからなるハムサンドイッチは、1回のカットで、3つの具材を同時に等分にできる!(パンが2枚のときは、2枚で1つの具材とカウント)
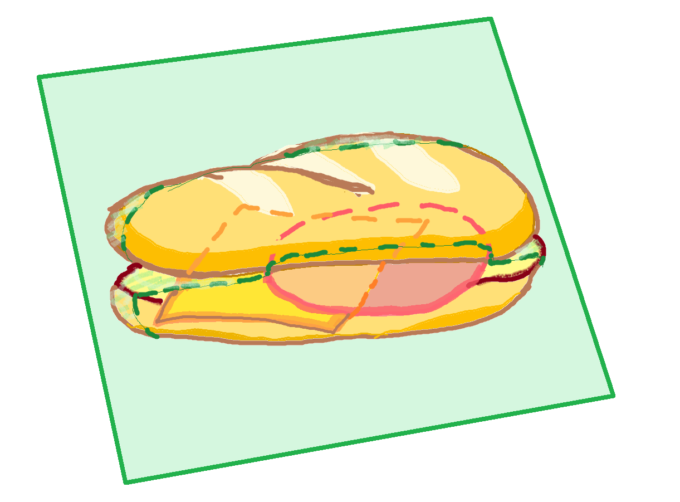
スイーツ派の方は、「いちごショートケーキの定理(一度のカットでいちごと生クリームとスポンジをすべて等分に分割できる!)」などと呼んでもよさそうです。
一般に、次の定理が成り立ちます。
\(n\)次元空間に\(n\)種の具材からなる\(n\)次元のサンドイッチがあるとき、\(n-1\)次元超平面による1回の切断で、\(n\)種の具材(の体積)をすべて等分に分割できる!
これらの定理をスマートに証明することができるのが、ボルスク・ウラムの定理です。
3.ボルスク・ウラムの定理
\(n\)次元球面\(S^n\)から\(n\)次元実数空間\(R^n\)への任意の連続関数\(f:S^n\rightarrow R^n\)に対して、ある \(x\in S^n\)において\(f(x)=f(-x)\)となる。(※1 対心点)
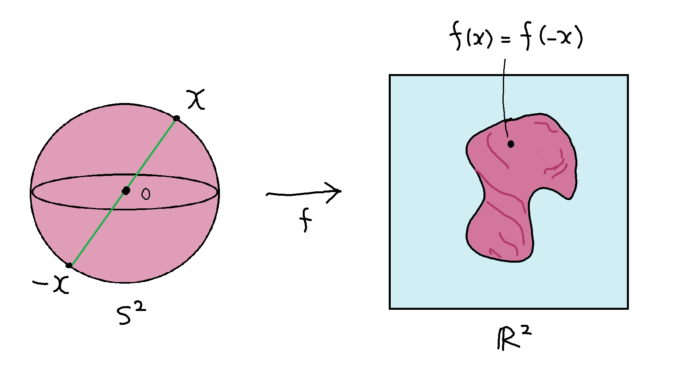
この定理はスタニスラウ=ウラムの定式化にもとづき1933年キャロル=ボルスクが最初に証明したとされています。

ウラム(左)、ボルスク(右)
定理を使うと、\(n\)次元サンドの2等分定理は次のように証明できます。
\(n\)種の具材を\(A_1,\cdots,A_n\)、\(n\)次元空間内の\(n-1\)次元超平面を\(a_1 x_1+\cdots + a_n x_n + a_{n+1}=0\) 、(ただし\(a_1^2+\cdots +a_{n+1}^2=1\))とする。 \(\vec{d}=(a_1,\cdots,a_n,a_{n+1})\in S^n\)であり、\(\vec{d}\)とその対心点 \(-\vec{d}\)は同じ超平面を表すが、法線ベクトルの向きが反対であることに注意する。
\(i=1,\cdots,n\)に対して関数\(f_i(\vec{d})\)を\(a_1 x_1+\cdots +a_n x_n+a_{n+1}>0\)の部分にある\(A_i\)の部分の体積と決める。\(\vec{d}=(0,…,0,1)\)は超平面を表さないが、任意の\((x_1\cdots ,x_n )\in R^n\)について\(a_{n+1}>0\)となるので、\(\forall i,f_i(0,…,0,1)=(A_i{\mbox 全体の体積})\)とする。\(\vec{d}=(0,…,0,-1)\)については、つねに \(a_{n+1}>0\)をみたさないので\(\forall i,f_i(0,…,0,-1)=0\)とする。
こうして連続写像\(f=(f_1,\cdots, f_n)∶S^n\rightarrow R^n, \vec{d}→(f_1(\vec{d}),\cdots, f_n(\vec{d}))\)が得られる。
ボルスク・ウラムの定理より、ある\(\vec{d}\in S^n\)において、\(f(\vec{d})=f(-\vec{d})\)が成り立つ。すなわち、各\(i=1,\cdots,n\)に対して\(a_1 x_1+\cdots+a_n x_n+a_{n+1}>0\)にある\(A_i\)の体積と\(-a_1x_1-\cdots-a_n x_n-a_{n+1}>0\)にある\(A_i\)の体積が一致する。後者は\(a_1 x_1+\cdots+a_n x_n+a_{n+1}<0\)を意味するので、この超平面によって、\(n\)種すべての具材が等分される。
4.地球上には、真裏と同じ気温と気圧の地点が存在する
ボルスク・ウラムの定理(\(n=2\))の言い換えとして、次のような表現が有名です。
気温と気圧でなくても、標高と湿度など、連続な2つの実数値関数なら何でも成り立ちます。また「ビーチボールを(くしゃくしゃに)潰して床に置くとき、1組の対心点で床上で重なるものが必ずある」とも言い換えられます。
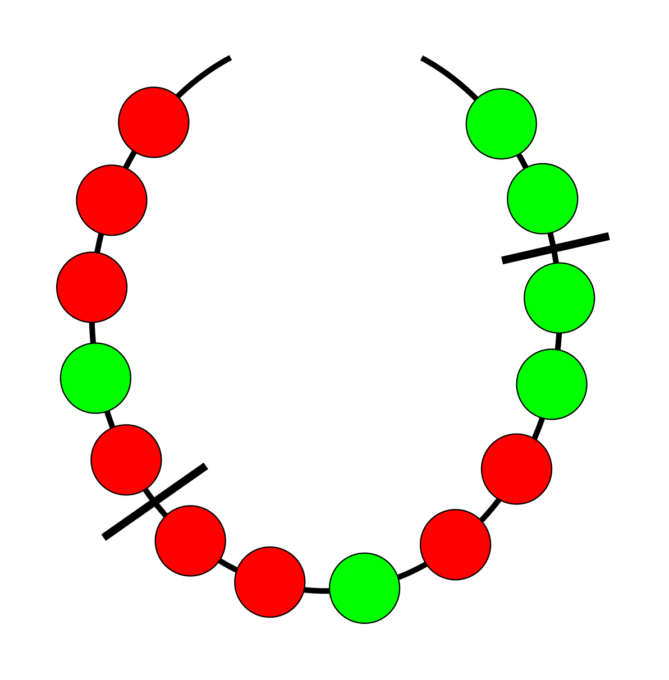
さらに、組み合わせ論や測度論に関係する「ネックレス分割問題」を解く際にもこの定理が有用です。「数種の宝石ビーズの繋がったネックレスを盗んだ泥棒たちが、同数ずつ宝石を分けるには最大何回ネックレスを切断しなければならないか?」という問題ですが、これもボルスク=ウラムの定理を使うことで、宝石の種類数×(泥棒の人数-1)回で十分という答えを導くことができます。
5.同値な定理が多数
この定理にはさまざまな数学的に同値な表現があります。
証明の際には、次のような「奇関数」(※2)を使った表現に持ち込んで示すことが多いです。
[代数トポロジー、ブラウワーの不動点定理の拡張]
[微分トポロジー]
そのほか、組み合わせ論における「タッカーの補題」、集合被覆論における「ルスターニク・シュニレルマンの定理」も、ボルスク・ウラムの定理と同値な定理です。
6.おわりに
どうでしたか。様々な形で表現される、非常に応用力の高い定理でしたね。
通常は代数トポロジーの手法で証明される定理ですが、ロマ数トレラン「微分トポロジー入門」では、「ジョルダンブラウワーの分離定理」のコラムでもお話した、\({\rm mod}\)2巻き数\(W_2 (f,0)\)に注目して、この定理を証明していきます!
<文/佐々木和美>
7.補足と参考
※1 対心点
\(x=(x_1,\cdots,x_{n+1})\in S^n=\{(x_1,\cdots,x_{n+1})\in R^{n+1}|x_1^2+\cdots +x_{n+1}^2=1\}\)に対して、\(-x =(-x_1 ,\cdots,-x_{n+1})\in S^n\)を\(x\)の対心点と呼びます。
※2 奇関数
写像\(g:S^n\rightarrow R^n\)がodd(奇関数)とは、任意の\(x\in S^n\)に対して、\(g(-x)=-g(x)\)(\(R^n\)のベクトルとして\(-1\)倍)が成り立つこと。
※3 odd retraction
連続写像\(f:S^n\rightarrow S^{n-1}\)がodd retractionとは、\(S^{n-1}\)を\(S^n\)の赤道、つまり、\(S^{n-1}=\{(x_1,\cdots,x_n,0)\in R^{n+1}∣ x_1^2+\cdots+x_n^2=1\}\)\(\subset S^n=\{(x_1,\cdots,x_{n+1})\in R^{n+1}∣x_1^2+\cdots+x_{n+1}^2=1\}\)とみたとき、連続写像\(f:S^n\rightarrow S^{n-1}\)で、\(S^{n-1}\)上で恒等写像(レトラクション)であり、かつ\(f(-x)=-f(x)\)(奇関数)であること。
ハムサンドイッチの定理
https://en.wikipedia.org/wiki/Ham_sandwich_theorem
ボルスク・ウラムの定理
https://en.wikipedia.org/wiki/Borsuk%E2%80%93Ulam_theorem
ネックレス分割問題
https://en.wikipedia.org/wiki/Necklace_splitting_problem