トポロジー有名定理その１～ブラウワーの不動点定理～

おすすめイベント・ゼミ

公開日

2021年10月4日

更新日

2021年10月4日

※universe PNG(トップ画像) Designed By 千图网 from Pngtree.com

※本記事はロマ数トレラン「微分トポロジー入門－境界付き多様体とmod 2交差理論－」の講師である佐々木和美先生によるトポロジーの有名定理の解説記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。

ロマ数トレラン「微分トポロジー入門－境界付き多様体とmod 2交差理論－」の詳細、お申し込みはこちらのページよりお願いいたします。⇒https://peatix.com/event/3014647/view

この記事の主な内容

1.はじめに

こんにちは。和から講師の佐々木です。ロマ数トレラン「微分トポロジー」に関連して、トポロジー分野で有名な定理を解説していきたいと思います。第1回目はブラウワーの不動点定理です。

コーヒーやみそ汁をかき混ぜてぐるぐる回る様子をぼーっと眺めていたことはありませんか。昔の数学者もぐるぐる回るコーヒーを眺め、そこから新たな定理を発見していたようですよ。

2.微分方程式からトポロジーへ

時は19世紀末、ヨーロッパの数学者の間では、太陽系の安定性問題という古い問題が再び取りざたされていました。惑星の公転軌道が長い年月の間に徐々にずれていき、いつか将来、太陽系が崩壊してしまうようなことはないのでしょうか。これは多体問題といい、微分方程式の解の安定性問題に帰着します。フランスのアンリ=ポアンカレは三体問題に取り組み、初期条件に基づいて厳密に解を書き下すことは不可能であり、わずかなずれが長時間たつと膨大な変化をもたらすという「カオス」の概念を発見したのでした。こうして微分方程式の解軌道の安定性を扱う「力学系」という数学分野の扉が開かれました。

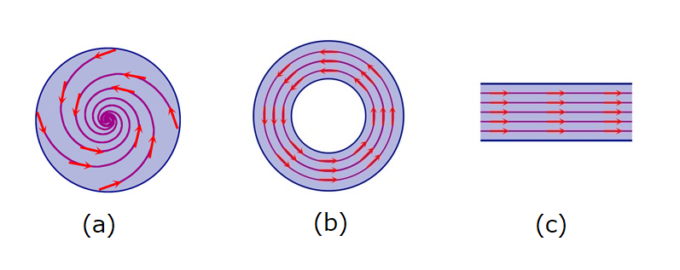
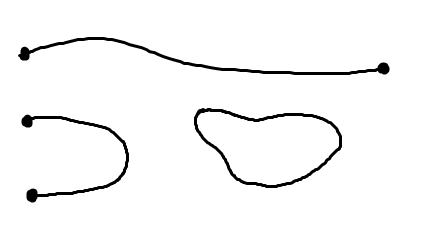
そんな折、かき混ぜたコーヒーの表面を眺めていたポアンカレは、きっとぐるぐる回る泡が太陽系の惑星たちに見えたのでしょう。コーヒー表面上の粒子の動きを曲面上の連続的なフローとみなし、力学系の理論を応用しました。軌道の様子は、曲面の位相的性質（topological properties）で決まります。コーヒーの表面領域は「コンパクト」つまり有界かつ閉集合なので、粒子は同じ周回軌道をぐるぐる回るか、もしくはある極限閉軌道（リミットサイクル）にどこまでも近づいていくかのどちらかです（ポアンカレ―ベンディクソンの定理）。ポアンカレはこの考えをさらに押し進め、円板型に同相な曲面(図(a))上のフローには必ず不動点が存在することを示しました。一方で、穴あき円板(図(b))や閉集合でない領域(図(c))では不動点は存在するとは限りません。これが「トポロジー」の始まりと言われています。（ポアンカレはこの新しい数学をanalysis situs（位置解析）と呼びました）

3.\(n\)次元閉球体から自分自身への連続写像は必ず不動点を持つ

ブラウワーの不動点定理
\(n\)次元球面体\(D^n\)から\(D^n\)への任意の連続な写像は必ず不動点(固定点)を持つ。

　
それからしばらく後の20世紀初頭、オランダの数学者L. E. J.ブラウワーも角砂糖を入れたコーヒーをかき混ぜながら、同じようなことを考えていました。ポアンカレの「位置解析」に影響を受けたブラウワーは、1910年、連続写像の「写像度」がホモトピー不変であることを用いて、上の定理が任意の次元で成り立つことを証明しました。ぐるぐる回るコーヒーの表面に定理を適用すると、「ある瞬間と、その\(\Delta t\)秒後で同じ位置にあるコーヒー粒子が少なくとも１つ存在する」ことを意味します（\(\Delta t\)は0.1秒でも1分でも構いません)。ここで言う「不動点（固定点）」とは、連続力学系（フロー）の不動点とは意味が異なるので注意してください。\(\Delta t\)秒後に同じ位置に戻ってくるのは「動いている」点かもしれません。

右の男性がブラウワー

4.定理の意味

\(n\)次元閉球体\(D^n\)とは、\(n=1\)のとき線分、\(n=2\)のとき円板、\(n=3\)のとき球体を指しますが、形は多少いびつでも、凸型でなくても（位相同型であれば）この定理は成り立ちます。また、写像は全射や単射でなくてもよく、不動点は1点とは限りません。

ブラウワーは次のような様々な言い換えで定理を説明したと言われています。

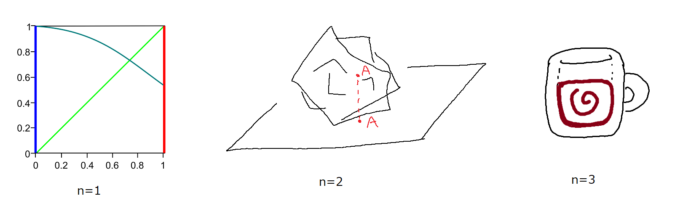
1.\([0,1]\)区間から\([0,1]\)区間への連続関数\(f:[0,1]\rightarrow [0,1]\)のグラフは必ず、対角線\(y=x\)と交点を持つ。（\(n=1\)の言い換え）（\(g(x)=f(x)-x∶[0,1]\rightarrow R\)に対して中間値の定理を使うと証明できる）

2.同じ地図を2枚用意し、1枚をくしゃくしゃに丸めてもう１枚の上に載せる。このとき、地図上の同一地点でちょうど上下に重なる点が存在する（\(n=2\)の例）

3.カップ内のコーヒー全体を上下にかき混ぜるとき、その前後でまったく位置が変わらないコーヒー粒子が存在する。（\(n=3\)の例）

5.応用と証明

ブラウワーの不動点定理は数ある不動点定理のなかでも、もっともよく知られている定理です。ジョルダン閉曲線定理、毛球の定理、ボルスク・ウラムの定理とともに、ユークリッド空間のトポロジーを特徴づける重要な定理であり、ゲーム理論や経済学の一般均衡理論における応用が有名です。

ブラウワーの不動点定理の証明のほとんどは、まず連続写像\(f:D^n\rightarrow D^n\)が不動点を持たないと仮定して\(D^n\)からその境界\(\partial D^n (=S^{n-1})\) へのレトラクション(※)を構成するところから始めます。そうしておいて、そのようなレトラクションの存在から矛盾を導くことができれば、背理法により、不動点の存在が証明されます。矛盾を示す方法としては、ホモロジー群、ストークスの定理、組み合わせ論（Sperner’s lemma）など、様々な手法がありますが、ロマ数トレラン微分トポロジー入門では、上記のレトラクションにおいて正則値の逆像が境界付き1次元多様体になることを用いるモリス＝ハーシュによる証明をご紹介します。

※位相空間\(X\)の部分集合\(A\)に対して、\(X\)から\(A\)へのレトラクションとは、連続写像\(f:X\rightarrow A\)で、\(f∣_A={\rm id}_A\)（\(A\)上で恒等写像）かつ\(f≃{\rm id}_X\) (恒等写像にホモトピック)が成り立つものをいう。