こんにちは。和からの数学講師の岡本です。今回は前回にひきつづき、三角形の合同について本気出して考えてみることにします。前回の記事はこちらをご覧ください。

合同条件について本気出して考えてみた～前編～

三角形の合同条件は以下の３つでした。
・３つの辺の長さがそれぞれ等しいとき
・２つの辺の長さとその間の角度がそれぞれ等しいとき
・１つの辺の長さとその両端の角度がそれぞれ等しいとき
つまり、２つの三角形は、上記3つのうち一つでも満たしていれば合同であるといえるのです。

１．３つの辺がそれぞれ等しいとき、本当に合同なのか？

まずは1つ目の合同条件についてです。３つの辺の長さが等しければ、本当に合同であるといえるのでしょうか？検証してみましょう。
これは３つの辺の長さを指定することでできる三角形が、合同なものを除いてただ一つに定まることを証明できれば十分です。実際に三角形の底辺の長さを\(a\)、その他の長さを\(b,c\)と指定してみます。

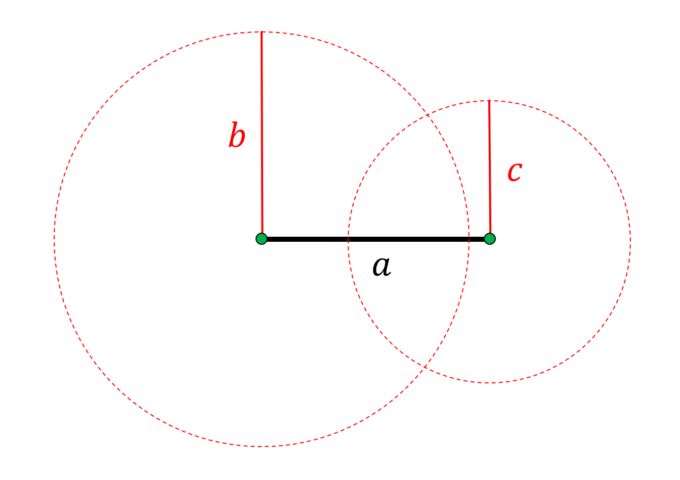
上の図のように底辺を固定し、両端の点からあらゆる方向に\(b\)、\(c\)進んだ位置を、円を使って考えます。つまり、これら2つの円の交点が指定した三角形の頂点になります。

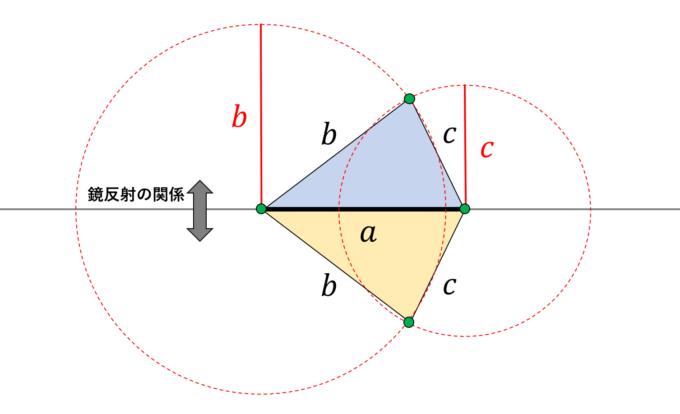
しかし、長さを指定した三角形は図のように2種類存在します。しかし、円の対称性から、上の三角形と下の三角形は鏡反射の関係になっていることがわかります。本来の合同の定義により、上下の三角形は合同となり、結果として「3つの辺の長さを指定してできる三角形は合同なものを除いてただ1つに定まる」ということが実証できました。
※もちろんどんな３つの数字の組でもいいわけではありません。図のように、交点を持つことが条件となります（三角形の成立条件）。

２．残り２つの条件との関係について

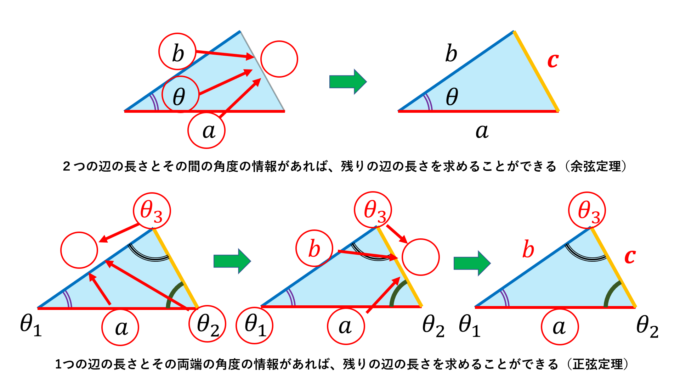
１つ目の条件と残りの条件との関係について補足しておきます。高校数学で習う「\(\sin, \cos\)」を使うことで、これらの関係を結び付けることができます。
まず、2つの辺の長さとその間の角度がわかっていれば、\(\cos\)を用いた「余弦定理」によりもう１つの辺の長さが定まります。したがって、2つの辺の長さとその間の角を指定すれば、3つの辺の長さがわかるので、先ほどの議論により、三角形が1つに定まります。
また、1つの辺の長さと3つの角度がわかっていれば、\(\sin\)を用いた「正弦定理」により、全ての辺の長さが定まります。よって、１つの辺の長さとその両端の角を指定すれば、３つの辺の長さがわかるので、同様に三角形が1つに定まります。

３．「両端の角度」と「間の角度」

３つ目の条件では、「1つの辺の長さとその両端の角度」について言及していますが、別に「両端の角度」である必要はありません。実際にどこか2つの角度がわかっていれば、三角形の内角の和が180度であることから自動的に3つ目の角度が求められるからです。なので、もう少し自由度を上げた書き方をするならば、「1つの辺の長さと２つの角度が等しいとき」となります。
　では、2つ目の条件「2つの辺の長さとその間の角度」についてですが、「間の角度」である必要はあるのでしょうか？

実は「間の角度」でなくてはいけません！実際に「2つの辺の長さと、その間ではない角度」を指定することで三角形が一つに定まるかどうかを考えてみます。
図のように、底辺の長さ\(a\)を固定し、右端の角度\(\theta\)を固定し直線\(L\)を描きます。また左端を中心とした半径\(b\)の円を描いてみます。

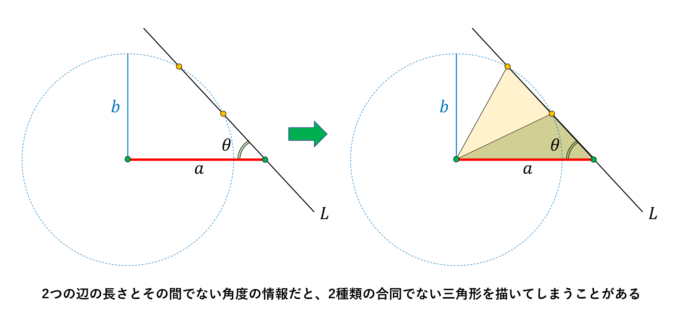
直線\(L\)と円の交点がある場合、三角形が成立します。図を見ると、この交点は2点で交わるか、1点で接するかの2通りになります。2点で交わる場合、お分かりのように条件を満たす（つまり、2つの辺の長さが\(a, b\)で、その間にない角度が\(\theta\)であるような）三角形が2通りできることがわかります。これにより、合同条件は「2つの辺とその間の角度」を見ないと十分でないことが確認できました！
なお、1点で交わる場合は直角三角形となり、特殊な場合です。いずれにしても、「2つの辺とその間でない角度」の情報では、不十分であることがわかります。

４．さいごに

いかがでしたでしょうか。三角形の合同条件という、中学校以来ほぼ目にすることはない素朴な題材ですが、考えれば考えるほど奥が深く面白い話に結びつきます。今後もこのような題材があれば解説していきたいと思います。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>

レイメイ藤井 ペンパス シャープタイプ グリーン JC903M
市販のシャーペンの芯を使えるオススメコンパスです！