こんにちは。和からの数学講師の岡本です。今回は「三角形」の合同条件について本気出して考えてみたいと思います。こうした図形に関する論理や証明といった話題は、中学校で初めて現れ、多くの方を苦しめたことでしょう。しかし、社会に出て大人になったいま、もう一度振り返ってみると、意外と面白い世界が見えてくるかもしれません。

１．三角形が同じであるとは？

そもそもの話からはじめましょう。「図形が同じ」であることを数学では「合同」といいます。例えば次のような図形AとBは同じ図形であり、合同であるといえます。

しかし、「図形の合同」とは意外にも難しい概念であり、正確に以下のように説明されます。

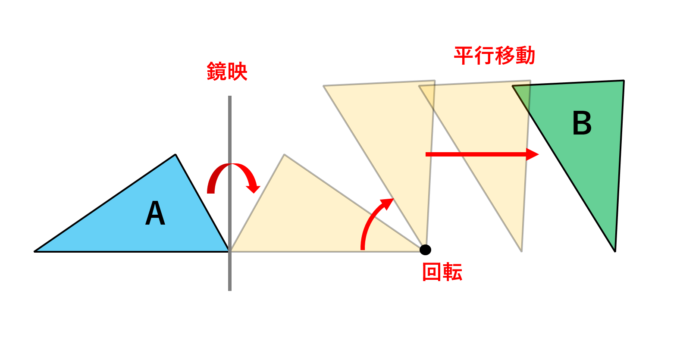
「平行移動」とはその名の通り、図形を平行に移動させることです。また、回転とは、どこかの１点を固定し、そこを中心に図形を回転させることを意味します。最後の「鏡映」とは、どこかに直線を固定し、その線を境界として図形を鏡反射させる操作のことを言います。
簡単な絵を描いたのでこれを参考にしてください。

２．三角形の個性

上で説明した内容は2次元平面内のどんな図形に対しても「合同」という概念を考えることができます。しかし、三角形などの構造が簡単な図形に対しては、「合同」であることを「平行移動」「回転」「鏡映」という言葉を使わなくても説明することができます。
実際に三角形の“個性”は「辺の長さ」と「角度」で決まります。また三角形はそれぞれ3つずつの情報を持っているので、合計で6つの特徴が同じであると言えば、２つの三角形が“同一人物”であることが説明できます。しかし、6か所の情報を全て確認しなけらばならないでしょうか？

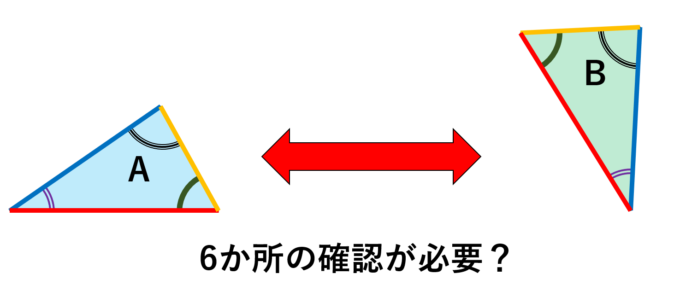
例えば、三角形の内側の角度（内角）の和は必ず180度であることを知っていれば、2つの角度の情報から自動的に３つ目の角度がわかります。
このように、三角形の特徴を部分的に見るだけで２つの三角形が“同一人物”であることがわかります。

つまり、合同であることを図形の変換（平行移動や回転、鏡映）という、ある意味「大域的な特徴」をみるまでもなく、長さや角度といった「局所的な特徴」を数か所確認するだけで十分説明できるというのです。よくよく考えると感動しますね！！

３．三角形の合同条件

さて前節では2つの三角形が同じかどうかを確認するのに、６つ全ての特徴を見る必要はないという説明をしました。では必要最小限の特徴はどこを見ればいいのでしょう？実はこれをまとめたのが、中学校で現れた次の「三角形の合同条件」です。

① 3つの辺の長さが同じかどうか
② 2つの辺の長さとその間の角度が同じかどうか
③ 1つの辺の長さとその両端の角度が同じかどうか

上の①～③うち、１つでもクリアしたら、2つの三角形が「合同」であるといえるのです！
こちらもわかり易いように図の説明を入れておきましょう。

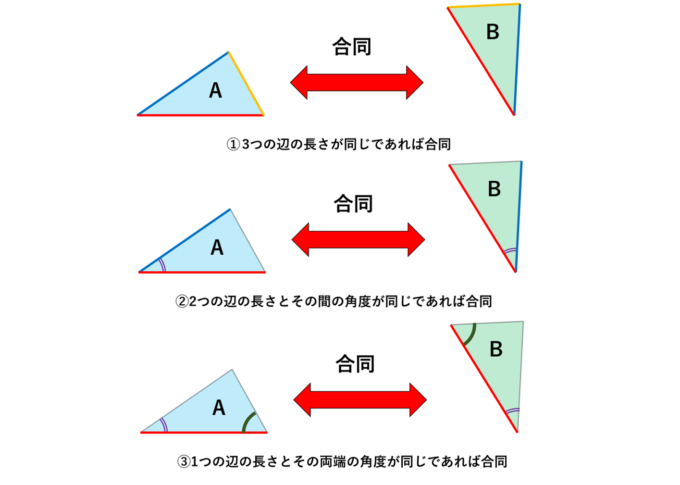
素晴らしいですよね！①～③も結局はたった3つの特徴に注目すれば三角形が合同かどうかわかります！

４．さいごに

しかし、これをなんとなく許容してそのまま使うのはあまりにももったいない題材です。
次回は「この条件が本当に合同であることを説明できるのか？」「その他の条件だとまずいのか？」などといった点について解説していきます！お楽しみに！

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>

おしゃれ 真鍮製定規