動画で見たい方はこちら↓↓↓

和から講師の松中です。先日、講師の岡本が三角形の合同条件について取り上げました。

合同条件について本気出して考えてみた～前編～

三角形は合同条件によりその形、大きさが一意に定まります。つまり、合同条件により三角形の面積が決まるはずです。本記事では合同条件に出てくる辺の長さや角度の大きさからどのように三角形の面積が求めるかをまとめてみました。どれも高校数学レベルで簡単に求めることができますが、有名と思われる順番に紹介していきます。

2辺とその間の角がそれぞれ等しい

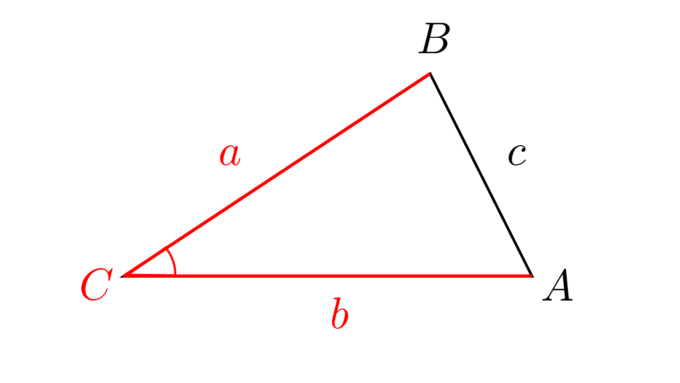
三角形${\rm ABC}$の辺$a$、$b$の長さと角$C$の大きさが分かっているものとします。このとき$\sin$の定義から、以下の図のように$b$を底辺とする三角形の高さは$a\sin{C}$であることが分かります。

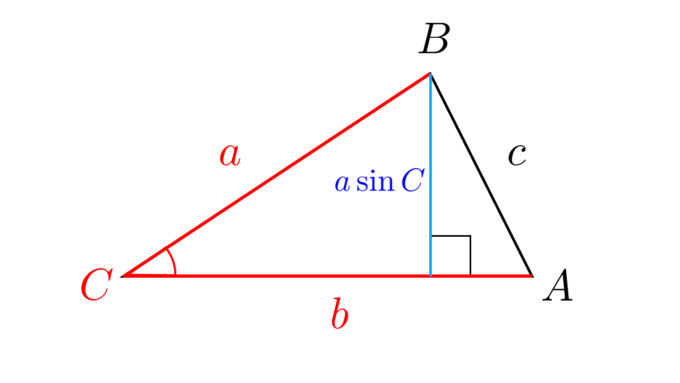
よって、三角形の面積$S$は(底辺)×(高さ)÷2を計算することで、

$$S=b\times a\sin{C} \div 2 = \frac{1}{2}ab\sin{C}$$
として求まります。たしかにこの公式には最初に与えられた2辺の長さ$a$、$b$と角の大きさ$C$だけが出てきており、三角形の合同条件に対応していることが分かります。

3辺の長さがそれぞれ等しい

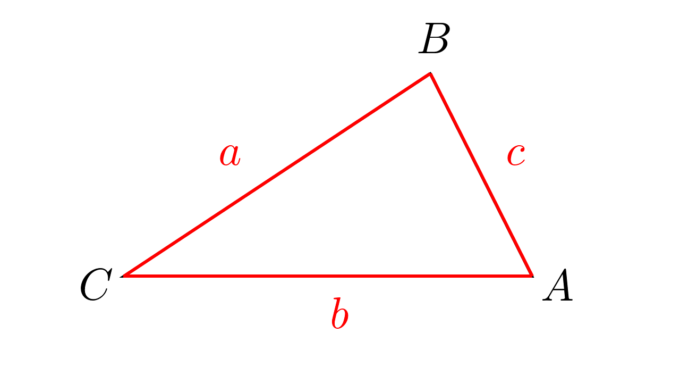
三角形${\rm ABC}$の3辺の長さ$a$、$b$、$c$が分かっている時に、三角形の面積は以下のヘロンの公式で求めることができます。

　
この証明は先に紹介した「2辺とその間の角がそれぞれ等しい」に対応する面積の公式$S=\frac{1}{2}ab\sin{C}$から簡単に証明できます。

まず、余弦定理から、

$$\cos{C}=\frac{a^2+b^2-c^2}{2ab}$$
です。これから
$$\sin{C}=\sqrt{1-\left(\frac{a^2+b^2-c^2}{2ab}\right)^2}$$
となり、$S=\frac{1}{2}ab\sin{C}$に代入し整理していくと、
$$S=\frac{1}{2}ab\sqrt{1-\left(\frac{a^2+b^2-c^2}{2ab}\right)^2}=\frac{1}{2}\sqrt{(ab)^2-\left(\frac{a^2+b^2-c^2}{2}\right)^2}\\ =\frac{1}{2}\sqrt{\left(ab+\frac{a^2+b^2-c^2}{2}\right)\left(ab-\frac{a^2+b^2-c^2}{2}\right)}\\ =\frac{1}{2}\sqrt{\left(\frac{a^2+2ab+b^2-c^2}{2}\right)\left(\frac{c^2-a^2+2ab-b^2}{2}\right)}\\ =\frac{1}{2}\sqrt{\left(\frac{(a+b)^2-c^2}{2}\right)\left(\frac{c^2-(a-b)^2}{2}\right)}\\ =\frac{1}{2}\sqrt{\frac{(a+b+c)(a+b-c)}{2}\frac{(c+a-b)(c-a+b)}{2}}\\ =\sqrt{\frac{a+b+c}{2}\frac{a+b-c}{2}\frac{c+a-b}{2}\frac{c-a+b}{2}}\\ =\sqrt{\frac{a+b+c}{2}\left(\frac{a+b+c}{2}-c\right)\left(\frac{a+b+c}{2}-b\right)\left(\frac{a+b+c}{2}-a\right)}\\ =\sqrt{s(s-a)(s-b)(s-c)}$$
が成り立つことが分かります。一見複雑な式変形ですが、和と差の積の公式$(a+b)(a-b)=a^2-b^2$を用いることで、簡単に変形できました。ヘロンの公式が「3辺がそれぞれ等しい」という合同条件に対応する公式であるということは考えたことがなかったので、楽しいです。

1辺とその両端の角

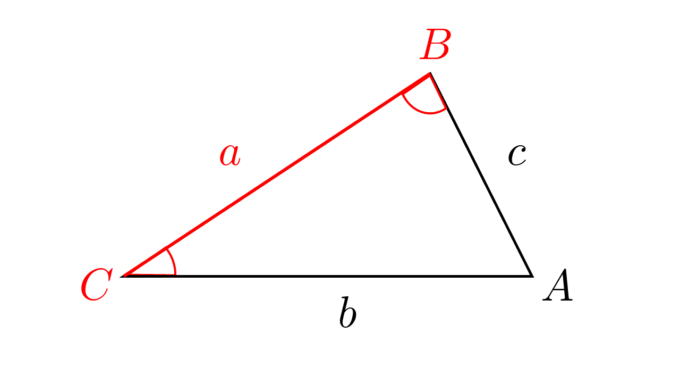
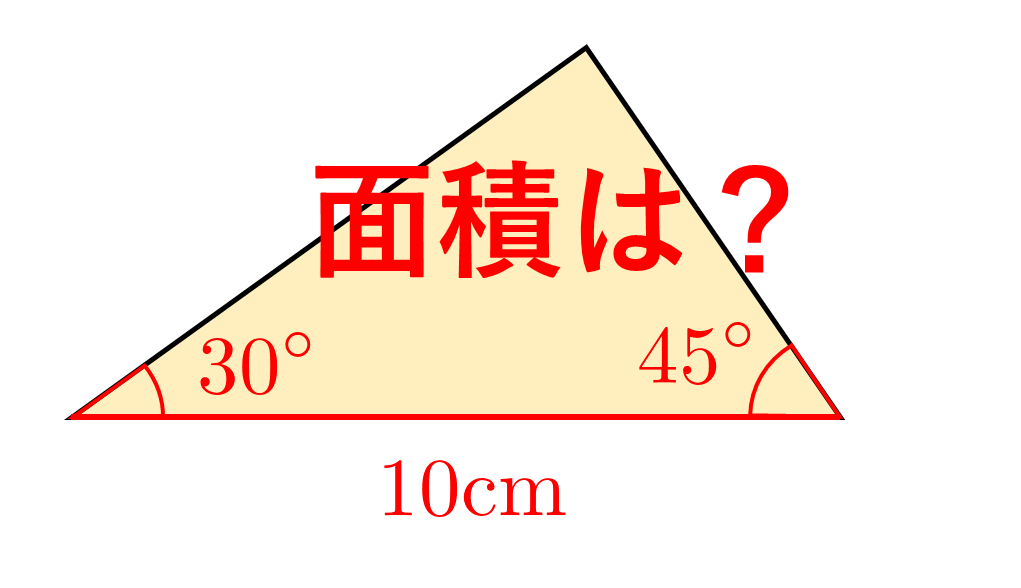
最後に三角形${\rm ABC}$の1辺の長さ$a$とその両端の角$B$と$C$の大きさが与えられているときの三角形の面積の公式を求めましょう。

こちらも結局$b$か$c$の長さが分かれば最初に紹介した「2辺とその間の角がそれぞれ等しい」の公式に帰着できます。

そして$b$の長さは正弦定理

$$\frac{a}{\sin{A}}=\frac{b}{\sin{B}}$$
を使えば簡単に求めることができます。

この式で$A$は分かっていませんが、三角形の内角の和は$180^\circ$ですから、$A=180^\circ-B-C$となり、

$$b=a\frac{\sin{B}}{\sin{A}}=a\frac{\sin{B}}{\sin{(180^\circ-B-C)}}=a\frac{\sin{B}}{\sin{(B+C)}}$$
として$b$が求まります。

あとは「2辺とその間の角がそれぞれ等しい」の公式を使えば、

$$S=\frac{1}{2}ab\sin{C}=\frac{a^2\sin{B}\sin{C}}{2\sin{(B+C)}}$$
となり、面積を求めることができました。こちらにも$a$、$B$、$C$以外出てきていませんし、$B$と$C$がちゃんと対称の形で出てきており、それなりに美しく感じます。

まとめ

今回は三角形の合同条件とそれに対応する面積の公式というあまり教科書では見かけない関係について調べてみました。試験などでいち早く三角形の面積を出したいときはこの公式を思い出していただければと思います。

　
<文/松中>

■本記事で登場した$\sin$、$\cos$を詳しく知りたい方は、こちらの講座がおすすめです。

三角比