こんにちは。和からの数学講師の岡本です。ここまでお話した「石取りゲーム」ですが、前回のお話にもあったように、後手必勝型を見つけ出すことが勝利への道筋でした。その道筋を照らす光こそGrundy数なのです。

石取りゲームにおける「神の一手」、いよいよ降臨です。

１．Grundy数の復習

　さてまずGrundy数の復習からいきましょう。Grundy数とは各状況について定義できる非負整数です。定め方は、状況\(A\)の次に移りうる全ての状況\(A_1, A_2, \ldots, A_i\)を考えのそれぞれのGrundy数\(G(A_1), G(A_2), \ldots,G(A_i)\)を除く最小の非負整数を\(G(A)\)とします。
例えば、（2,2）の次に移りうる状況は(2,2), (2,0), (1,2), (0,2)であり、それぞれのGrundy数を同様の方法で計算し、

\begin{align*}G(2,1)=3, G(2,0)=2, G(1,2)=3, G(0,2)=2\end{align*}

であることがわかります。よって\(3,2\)を除く最小の非負整数は\(0\)となり、

\begin{align*}G(2,2)=0\end{align*}

が得られます。このGrundy数を使って戦局を読み解くことができるのです！

２．Grundy数の恐るべき性質

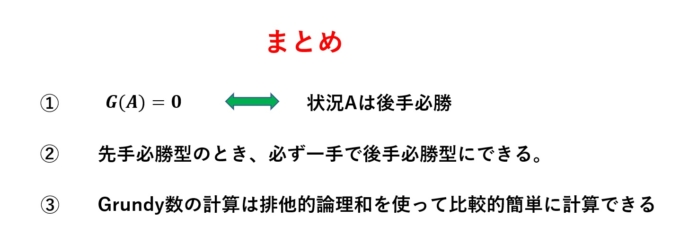
　何を隠そう、Grundy数が\(0\)の状況は「後手必勝型」となります！しかもGrundy数の定義から、\(G(A)=0\)という状況\(A\)から移りうる状況たちは全てGrundy数は\(0\)以外の数となり、「先手必勝型」となります。つまり、プレイヤーはGrundy数さえ計算できればゲームを完全に支配できるのです！
　しかしながら、Grundy数の計算は現実的ではなさそうな気がします。定義も複雑ですし、結局ゲーム終了時点から計算しなければならず、例えば\(G(7,5,3)\)なんて、途方もない計算量になってしまいます。

しかし！数学はやはり素晴らしい。なんとGrundy数には公式が存在します！このあたりを詳しく解説していきます。一山が１つの場合のGrundy数については次のような公式を得ていました：

\begin{align*}G(n)=n\end{align*}

実は、山が複数ある場合、特殊な演算「\(\oplus\)（排他的論理和）」を使って以下のような公式が得られます。

\begin{align*}G(n_1,n_2,\ldots,n_k)=G(n_1)\oplus G(n_2)\oplus \cdots \oplus G(n_k)=n_1\oplus n_2 \oplus \cdots \oplus n_k\end{align*}

さて、何やら見通しが良くなってきました。ではこの排他的論理和\(\oplus\)とはどういった計算なのでしょうか？次節で見ていきます。

３．排他的論理和とは

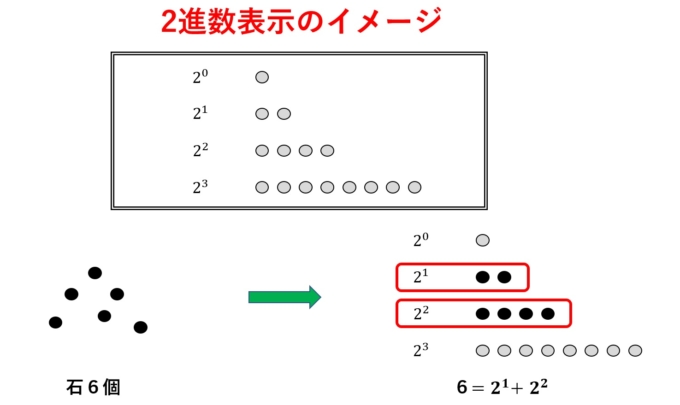
　２つの数\(3,5\)を用意します。この数に関して演算\(\oplus\)を計算してみます。まず。\(3,5\)をそれぞれ\(2\)進数表示します。\(2\)進数表示とは\(2\)の冪乗和で表すことを意味し、全ての自然数に対して考えることが可能です。例えば。

\begin{align*}3&=2+1=2^1+2^0=1\cdot 2^1+1 \cdot 2^0\Rightarrow11,\\
5&=4+1=2^2+2^0=1\cdot 2^2+0\cdot 2^1+1\cdot 2^0\Rightarrow10\end{align*}

と表現できます。対応しない冪の部分は0と表記してその他は１と表記して並べます。ちょうど、「係数」を並べるイメージです。

実は普段使っている数字は\(10\)進数表示であり、例えば

\begin{align*}3\cdot 10^2+1・\cdot 10^1+4\cdot 10^0＝314\end{align*}

という具合です。ひとまず\(3\)と\(5\)が\(2\)進数表示できました。\(10\)進法と混乱するので以降は\([1,1],[1,0,1]\)と表示することにします。では排他的論理和ですが、

\begin{align*}[1,1]\oplus[1,0,1]=[0,1,1]\oplus[1,0,1]=[0+1,1+0,1+1]=[1,1,0]\end{align*}

となります。つまり、各桁で足し算をします。さらにここでの足し算は

\begin{align*}0+0=0, 1+0=1, 0+1=1, 1+1=0\end{align*}

という計算をします。これは

偶数＋偶数＝偶数、奇数＋偶数＝奇数、偶数＋奇数＝奇数、奇数＋奇数＝偶数

を意味する演算です。とにかく、２進数表示の\([1,1,0]\)は10進数表示に直すと

\begin{align*}[1,1,0]=１\cdot 2^2+１\cdot 2^1+0\cdot2^0=6\end{align*}

となります。つまり

\begin{align*}3\oplus5=6\end{align*}

という不思議な演算ができました。これが排他的論理和です。

４．神の一手

３節の演算を使ってGrundy数を求めてみましょう。例えば、苦労して計算した\(G(2,2)\)については

\begin{align*}G(2,2)=2\oplus2=[10]\oplus[10]=[1+1,0+0]=[0,0]=0\end{align*}

となり、たしかに求められます！では３山の例で最初に扱った(7,5,3)はどうでしょう！

\begin{align*}G(7,5,3)&=7\oplus5\oplus3=[1,1,1]\oplus[1,0,1]\oplus[0,1,1]\\
&=[1+1+0,1+0+1,1+1+1]=[0,0,1]=1\end{align*}

となり、Grundy数が0でないので、先手必勝型の状況であることがわかります！！Grundy数が0にするためにはこの計算を注意してみると1桁目の1を一つ消せばいいので、例えば7個の山から１個石を取り6個にすれば

\begin{align*}G(6,5,3)&=6\oplus5\oplus3=[1,1,0]\oplus[1,0,1]\oplus[0,1,1]\\
&＝[1+1+0,1+0+1,0+1+1]=[0,0,0]=0\end{align*}

となり、後手必勝型となります！
つまり、Grundy数を計算することで勝利への道筋が与えられ、まさに「神の一手」が示されました！

驚くべき点は、どのような状況であってもGrundy数を計算することで、「0ならば後手必勝、0でないなら先手必勝」という具合に勝利までの道筋が保証されるという点です。もちろん、（「先手必勝型の状況で自分が先攻であること」または「そうでない状況（自分が不利な状況）で相手が必勝法をしらない」）かつ「Grundy数の計算を正しく行える」場合に限って勝利は保証されます。

５．さいごに

いかがでしたでしょうか？全部で4回にわたって連載してきました「石取りゲーム」の攻略法！今回ご紹介した石取りゲームは通称「二ム」と言われ、排他的論理和の事を「二ム和」と呼んだりします。また、「取れる石の数を限定する」「素数個しか取れない」など、石取りゲームのルールを変えても上の議論は成り立ち、Grundy数でゲームを支配することができます。美しい論理展開ですね。。。！今回取り上げた「石取りゲーム」の数学に関する参考書としては「石取りゲームの数学 佐藤文広 (著)」がおすすめです。

数少ない石取りゲームのディープな解説書です。興味のある方は是非ご覧ください。

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>