先手必勝！？戦略とゲーム理論（上級編その１）―Grundy数の計算―

ロマンティック

公開日

2020年10月10日

更新日

2020年10月10日

　こんにちは。和からの数学講師の岡本です。前回までにお話した「石取りゲーム」。ついに今回は数学的な解説をいたします。初級編、中級編はこちらからご覧いただけます。

初級編

先手必勝！？戦略とゲーム理論（初級編）

中級編

先手必勝！？戦略とゲーム理論（中級編）

この記事の主な内容

１．これまでの考察

　さて、これまでは２山の場合、３山の場合の考察を行ってきました。今回はまず、これらの考察をもう少し詳しく見ていきます。

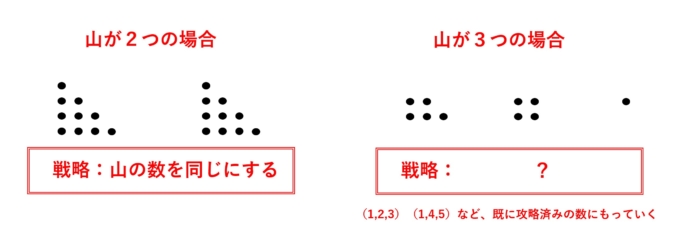
　２山の場合、「石の数を同じにする」という作戦が必勝法でした。これは言い換えると“同数２山”という状態が、「後手必勝である」ということを意味します。このような状態を後手必勝型と呼ぶことにしましょう。それ以外の状況であれば「うまい一手」により、後手必勝型にすることができます。
　３山の場合も２山と同様に、(1,2,3)や(1,4,5)などの「後手必勝型」があり、それ以外の状況であれば「うまい一手」次第で「後手必勝型」に塗り替えられえます。そのため後手必勝型でない状況を先手必勝型と呼ぶことにしょう。

実はこのゲームの初期配置は先手必勝型と後手必勝型の2通りしかありません。後手必勝型の配置では、どんな手を打っても必ず先手必勝型の配置になってしまい、先手必勝型の配置からは必ず後手必勝型に塗り返す一手が存在することが保証されています。少々わかりづらいネーミングですが、「先手必勝」、「後手必勝」というのは自分主体で考えます。つまり、「この状況であれば自分は先手がいいな」、「この状況であれば後手がいいな」といった具合です。

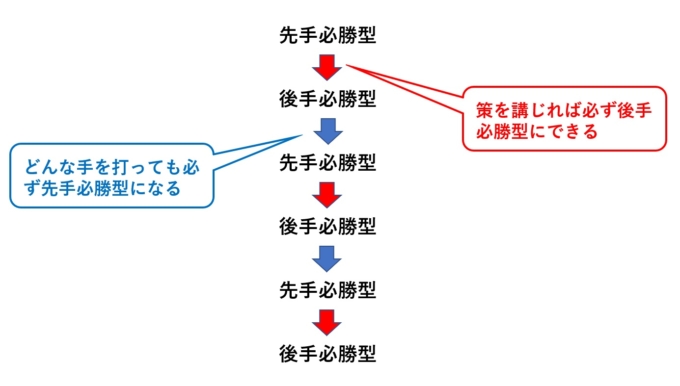
つまり、このゲームを支配するには「後手必勝型」を知ることがカギになるわけです。

２．戦局の把握

　後手必勝型や先手必勝型の状況を数学的にとらえていきましょう。とらえ方の基本は非常にシンプルで、「ゴール（ゲーム終了の状況）から考える」というものです。
例えば１山の場合、ゲーム終了の状況はもちろん石の数「0」。これを後手必勝型と考えます。「0」になる前の段階の候補は石の数が「1」、「2」、「3」、…と無数に考えられ、どの状況も先手必勝となります。

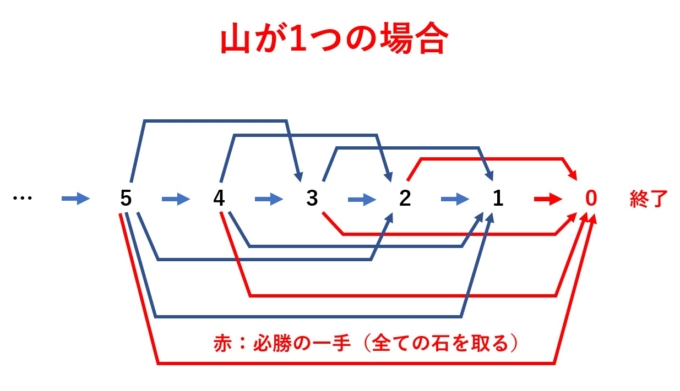
つまり、１山の場合は「0」という状況以外全て先手必勝型となっています（先攻のプレイヤーが全部の石を取ればゲーム終了となるので当たり前ですね）。では２山の場合はどうでしょうか。初級編で解説した通り、石の数が同数の状況が後手必勝型といえ、それ以外は全て先手必勝型となっています。これも先ほどと同様に「(0,0)」からはじめて、一手前、そのまた一手前という具合に候補を並べていきます。

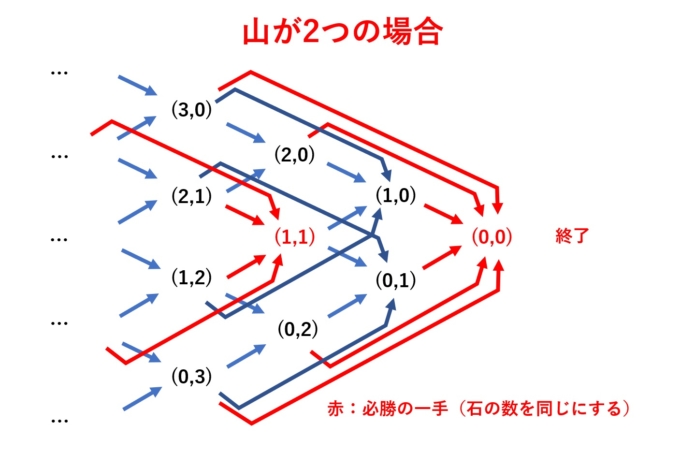
この図を踏まえて、戦局の状況を表す指標を次節で導入します。

３．戦局の道標―Grundy数―

　ではいよいよ、戦局を特徴付ける指標として「Grundy数」というものを各状況に対して定義します。Grundy数の定義は非常にクセが強いです。

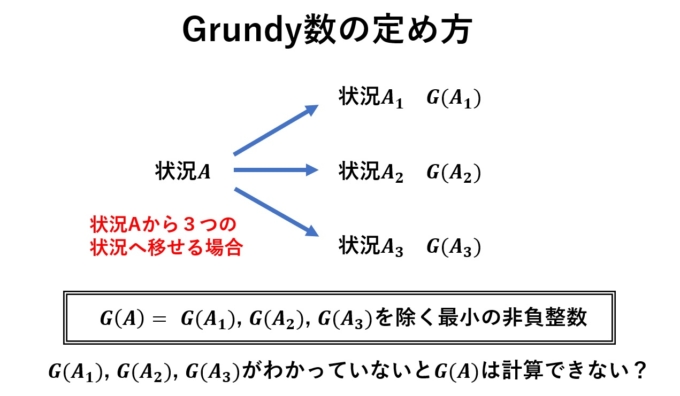
まず、ゲーム終了時点（後手必勝型）のGrundy数を「\(0\)」とします。続いて状況\(A\)のGrundy数を定義しましょう。その状況から移りうる状況たち（\(A_1, A_2, \ldots\)）のGrundy数を除く最小の\(0\)以上の整数（非負整数）を、状況\(A\)のGrundy数とします。つまり各Grundy数\(G(A_1),G(A_2),\ldots\)がわかっていないと\(G(A)\)は求められません。

例えば、１山の場合「0」の状況のGrundy数を\(G(0)=0\)と表すことにします。次に状況「１」を考えます。「１」という状況の次にくる状況は「0」のみです。\(G(0)=0\)なので、\(0\)を除く、最小の非負整数として\(G(1)=1\)が得られます。もう少し例を考えましょう。次に石の数が「2」の状況の場合、次の状況の候補は「1」と「0」の２通りあります（もちろん、「0」にすることで勝利ですが、あくまで、取りうる状況全てを考えます）。\(G(0)=0, G(1)=1\)なので、\(0\)と\(1\)を除く最小の非負整数として\(G(2)=2\)が得られます。同様に考えることで一般に

\begin{align*}G(n)=n\end{align*}

という公式が得られます

続いて２山の場合のGrundy数を考えましょう。まずゲーム終了時点の（0,0）のGrundy数を\(G(0,0)=0\)とします。次に状況(1,0)のGrundy数を求めます。まず(1,0)から移りうる状況は（0,0）のみなので、\(G(1,0)\)は\(0\)以外の最小の非負整数である\(1\)となります。同様に\(G(0,1)=1\)も求められます。続いて、\(G(1,1)\)を求めてみましょう。状況（1,1）から移りうる状況は（1,0）または（0,1）の２通りしかありません（これは石取りゲームのルールで、複数の山から石が取れないことから言えます）。\(G(1,0)=G(0,1)=1\)であることから、(1,1)のGrundy数は\(1\)を除く、最小の非負整数として、

\begin{align*}G(1,1)=0\end{align*}

となります。では\(G(2,2)\)はいくらになるでしょうか？状況（2,2）から移りうる状況を全てリストアップすると、(2,1), (2,0), (1,2), (0,2)の４通りとなります。１山の議論からまず\(G(2,0)=G(0,2)=2\)がわかります。また、（2,1）の状況の移りうる状況の候補は

\begin{align*}(2,0), (1,1), (0,1)\end{align*}

の３通りで、それぞれのGrundy数は

\begin{align*}G(2,0)=2, G(1,1)=0, G(0,1)=1\end{align*}

であるので、\(G(2,1)\)のGrundy数は\(2,0,1\)を除く最小の非負整数である\(3\)となります。
このことから

\begin{align*}G(2,1)=3, G(2,0)=2, G(1,2)=3, G(0,2)=2\end{align*}

となり、\(3,2\)を除く最小の非負整数は\(0\)であるので、状況(2,2)のGrundy数は

\begin{align*}G(2,2)=0\end{align*}