１．悲劇

悲劇は突然訪れました。

買ったばかり綿棒210本入りを、弊社スタッフの岡本は全て床にまき散らしてしまいました。。。絶望する岡本。床に散らばった綿棒を眺め、あることを思い出します。

\begin{align*} \text{円周率の近似計算できるじゃん…！} \end{align*}

２．涙の確率計算

床一面に広がる平行線（下の写真での青い線）に、散らばった綿棒たちが何本交わっているかを数えてみます。つまり写真の黄色で囲まれた綿棒を数えることになります。すると210本中104本が交わっていたことがわかりました。

これが本来どのぐらいの確率で起こるのか、気になりませんか？実は、この問題は「ビュッフォンの針の問題」といって計算することができます。早速紙とペンを用意し、計算をしてみましょう！

まずは状況把握。綿棒の長さは測ると78mm、また、床の平行線の幅は100mmでした。

一般的な状況で、次のような結果が成り立ちます。

ビュッフォンの針

もはやアートです。なんと確率に円周率が現れます。

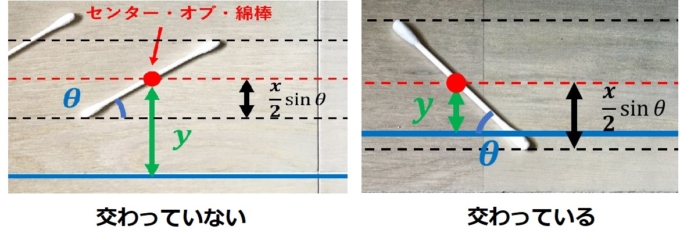
上の図のように、綿棒の状態は綿棒の中心部分（「センター・オブ・綿棒」と呼ぶことにします）の位置情報と角度\(\theta\)によって決定できます。このとき綿棒の中心からの先端までの「高さ」（図の黒い幅）は、なす角度\(θ\)を使って\(\frac{x}{2}\sin \theta\)と表すことができます。センター・オブ・綿棒から平行線までの距離を\(y\)とすると。「綿棒が交わる状態」を数式で表現することができます。

「綿棒が交わる」＝「緑\(\leq\)黒」＝「\(y\leq \frac{x}{2}\sin \theta \)」

つまり\(y\)と\(\theta\)をランダムにとってきて（もう少し正確な条件を述べるとどちらとも独立に連続一様分布に従っているとします。）\(y\)と\(\theta\)との関係が\(y\leq \frac{x}{2}\sin \theta\)となる確率が、求めたい「綿棒が交わる確率」です。

これは以下のような図を考えると視覚的にわかり易くなります。

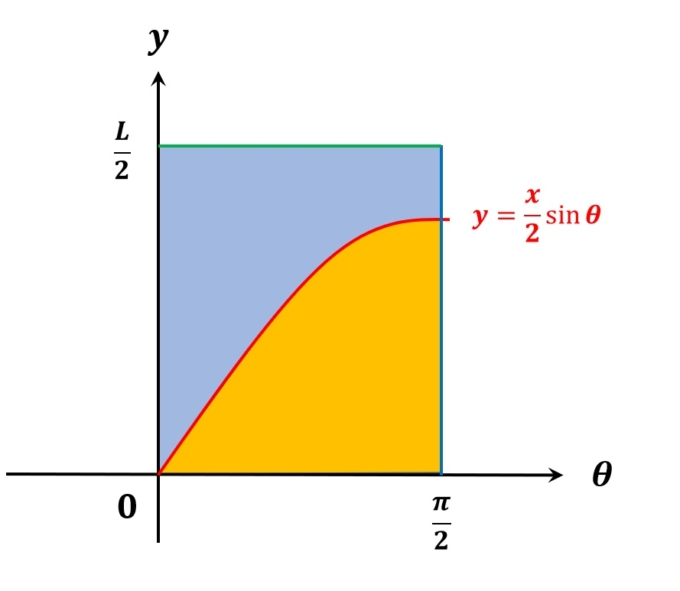
全体の長方形の面積は\(\frac{\pi}{2}\times\frac{L}{2}=\frac{\pi L}{4}\)となり、これは綿棒の状態全てを表しています。またオレンジ色に塗られた部分の面積は「綿棒が交わっている状態」を表し、積分を使って

\begin{align*} \int_0^{\frac{\pi}{2}}\frac{x}{2}\sin \theta d\theta=\frac{x}{2} \end{align*}

と求めることができます。すなわち、綿棒が重なる確率\(P\)は

\begin{align*} P=\frac{\frac{x}{2}}{\frac{\pi L}{4}}=\frac{2x}{\pi L} \end{align*}

と計算できます。

３．円周率を推定する

さて、今回の状況に合わせてみましょう。まず綿棒の長さ\(x=78\)、そして床の平行線の幅は\(L=100\)でした。これにより、綿棒が交わる確率は先の結果から

\begin{align*} P=\frac{2 x}{\pi L}=\frac{2\times 78}{\pi\times 100}=\frac{39}{25 \pi} \end{align*}

となります。今回落としてしまった綿棒が210本中104本交わったこの比率は確率\(P\)に近い値だろうと推測できます。逆に言うと、この結果から円周率の値を推測することができるのです！円周率\(\pi\)をわからないものとして、\(\pi\)に関する方程式を解いていきます。すると

\begin{align*} \frac{39}{25 \pi} \approx \frac{104}{210}\Leftrightarrow\pi \approx \frac{39 \times 210}{25 \times 104}=3.15 \end{align*}

となり、なんと円周率\(3.141592\cdots\)に非常に近い値をたたき出しました！

４．終わりに

いかがでしたでしょうか？床に落ちた綿棒から、なんとあの円周率を逆算することができました！皆さんも平行線のある床に細い棒状のものをたくさん落としてしまった場合、冷静になってまず円周率をどこまで近似できるか計算してみましょう。お掃除はそのあとです（もちろん冗談です）。

またこうした一見複雑そうに見えるものも計算をしてみれば結果的に非常にきれいな、そして円にまつわる比率「円周率」が現れることに岡本は数学のロマンを感じます。このような「結論の美しさ」は数学における一つのアートだと考えています。岡本による数学アートの無料セミナーも開講しましたので、気になる方はぜひご参加ください！(数学アート超入門-美しさの中の隠れた数学- https://wakara.co.jp/course/7803)

今回ご紹介した問題を取り扱っている本として「直感を裏切る数学　神永正博 著(ブルーバックス)」は非常におすすめで、ビュッフォンの針以外にもたくさんの面白い数学ネタが詰まっています。

<文/岡本健太郎>