\(\sqrt{4}=-2\)を実感する。多価関数への誘い。
公開日
2020年12月17日
更新日
2020年12月17日
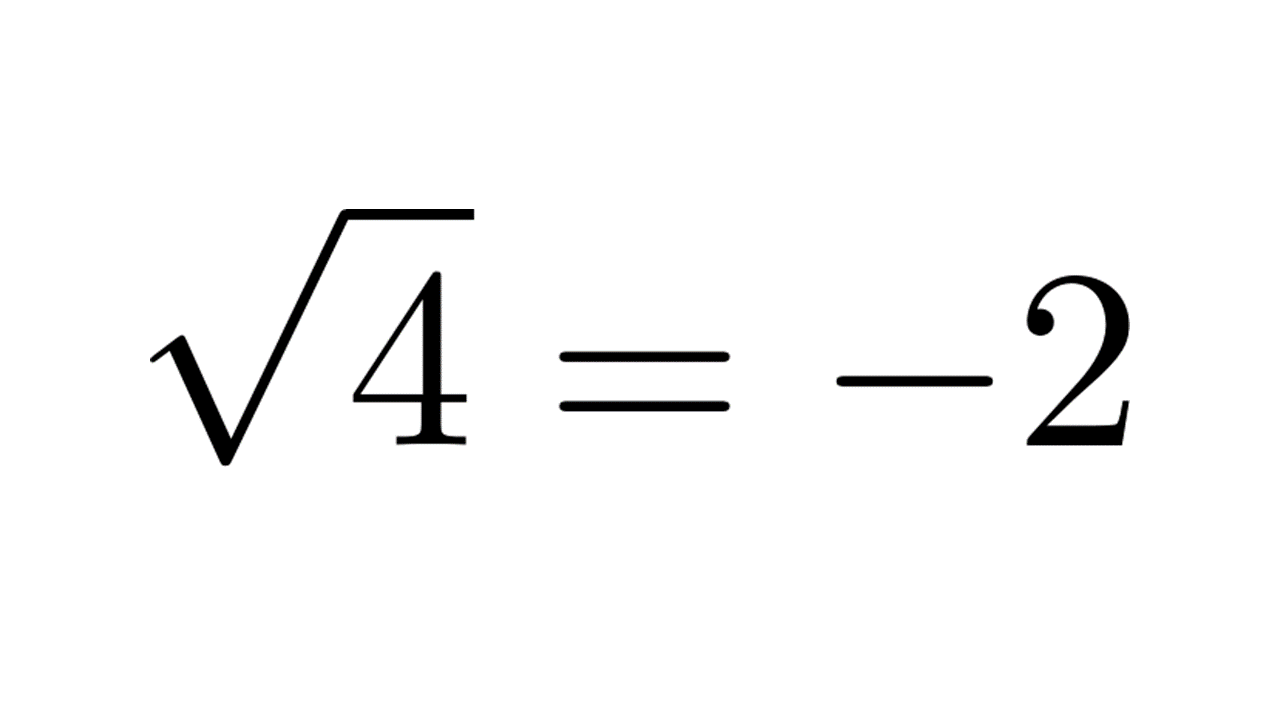
この記事の主な内容
公式よりも定義が大事
和からの松中です。
中学数学や高校数学の授業をする時に、私はよくお客様に「公式なんてどうでもよい。大事なのは定義。」とお話しします。
定義とは数学に出てくる記号や用語の意味を明確に書き下したものです。
「\(\sqrt{2}\)は無理数であることを証明せよ。」とか「二等辺三角形の底角は等しいことを証明せよ。」といった証明問題を解く際に、\(\sqrt{2}\)が何であるか、無理数が何であるか、二等辺三角形がどんな三角形であるかといった定義が曖昧なまま「問題が解けない」と頭を悩ませる方が一定数いらっしゃいます。定義を意識することで何を前提に何をしないといけないのかがはっきりわかります。頭を悩ませるのはそれからにしましょう。
一方、公式とは、その公式よりもっと当たり前の事実や別の公式から証明できるものです。上の「\(\sqrt{2}\)は無理数である」、「二等辺三角形の底角は等しい」も少し違和感がありますが公式といってもよいでしょう。
\(\sqrt{2}\)や無理数が何かよくわかっていないのに、「\(\sqrt{2}\)は無理数である」とかっこつけて言っても何の説得力もないでしょう?
また、\(\sin\)の加法定理\(\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}\)を知っていて、使いこなせていても、\(\sin\)、\(\cos\)が何かわからなかったらかっこ悪いですよね?
1999年の東大の入試試験に「\(\sin\)、\(\cos\)の定義を述べよ」という問題が出題されたそうです。定義の大事さが分かりますよね。
8年前の自分の投稿
本記事をここまで書いて思い出したのですが、昔マクドナルドで見ず知らずの高校生のカップルに勝手に数学を教えたことがあります。自分のFacebookを探したら当時の記録が残っていました。
2012年11月29日の投稿です。(「公式よりも定義が大事だ」と、8年前と全く同じこと言っていて少し驚きました。)
隣の席では高校生カップルが数学のテスト勉強していました。
わからないという言葉が何度も聞こえてきたので、
通りすがりの数学者を名乗り、
一時間ばかり3人で数学の世界を楽しみました。
見ず知らずの人が急に話してくると怪しまれる世の中ですが、
数学の力で年代、性別の壁を超えました。
「公式」を覚えることが大事、といった教育を受けているみたいですが、
数学において本当に大事なのは「定義」です。
sin(サイン)の「定義」が曖昧なまま、「公式」を使って三角比の問題を解いても意味がありません。
テストが終わり「公式」を忘れてしまえば、何のためのテスト、何のための「公式」でしょうか。
「定義」を明確に理解する
→いままで意味も分からず「公式」として使っていたものの意味を知る
(→感動する)
→「公式」を使って問題が解ける
このプロセスを繰り返しました。
意味を伴う「公式」は簡単に忘れませんし、
忘れても「定義」から自分で産み出せます。
「すご~い」と何度も言ってもらえたので、
きっと感動してくれたんだと思います。
8年前の自分も言っているように、「公式」なんて導出できるものだから重要とは思いません。(もちろん高校入試、大学本番はスピード勝負なので、短時間で答えが出せる公式は重要にはなるので強くは言えません。)
平方根と\(\sqrt{\,\,\,\,\,}\)の違い
中学数学を教えているときに、殊更定義を強調するのは平方根とルート(\(\sqrt{\,\,\,\,\,}\))に対してです。
平方根とルートはとても似ていて、間違える方が多くいらっしゃいます。
それぞれ定義を見ていくと、
\(0\)以上の実数\(a\)に対して、\(2\)乗したら\(a\)になる数を\(a\)の平方根という。
正の実数\(a\)に対して、\(a\)の平方根のうち正のものを\(\sqrt{a}\)と書く。また、\(\sqrt{0}\)は\(0\)と定める。
となります。
例えば\(4\)の平方根とは、\(2\)乗して\(4\)になる数のことなので、\(2\)と\(-2\)になります。また、\(\sqrt{4}\)は\(4\)の平方根のうち正のものなので、\(2\)となるのです。
平方根は2つあるのに、\(\sqrt{\,\,\,\,\,}\)は1つしかないというのはなんだか不公平で\(-2\)がとてもかわいそうです。でも安心してください。\(-2\)のような負の平方根もルートを使って\(-\sqrt{a}\)と書くことができます。めでたしめでたし。。。
と、中学数学の授業だとこれだけの解説で終わるのですが、それでもやはり\(-2\)の不公平感は否めません。\(\sqrt{\,\,\,\,\,}\)というかっこいい新しい記号を用意したのに、自分はおまけのように\(-\sqrt{4}\)と書かれてしまう。\(2\)と\(-2\)で正の\(2\)の方が偉いなんて誰が決めたのでしょうか。
それを決めたのは神様でも仏様でもなく、本当にただの人間です。\(\sqrt{a}\)が\(a\)の正の平方根というのは本当にただのちっぽけなルールなのです。
多価関数登場
先述した通り、\(\sqrt{4}=2\)、\(\sqrt{4}\neq -2\)では\(-2\)があまりにかわいそうです。しかも\(-2\)をかわいそうな存在にしてしまったのは数学的な必然性によるものではなく、人間が決めたただのルールです。高校までであれば「かわいそうだけど仕方がない」で済ますしかないのですが、大学で複素関数を学ぶと\(-2\)に希望の光が降り注ぎます。
\(-2\)に希望の光をもたらす存在、それは多価関数です。

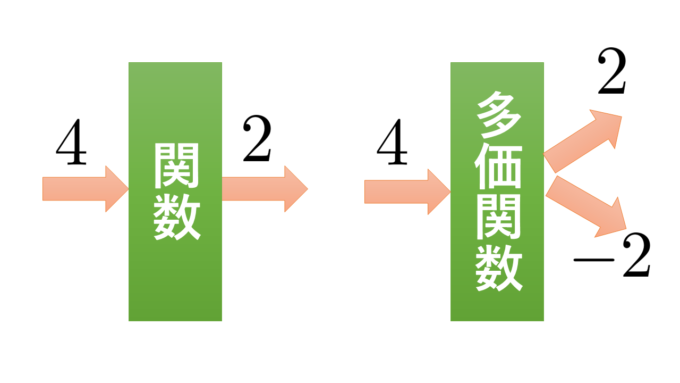
関数は中学数学以来\(x\)をいれると\(y\)が出てくるルールとして定義されていました。入力\(x\)に対して出力\(y\)は一意的に決まるのが関数のルールです。
一方、大学の複素関数で学ぶ多価関数は、同じ入力に対して2つ以上の出力を許します。そして、実は\(\sqrt{\,\,\,\,\,}\)は複素関数の世界では2つの値を返す多価関数になるのです。つまり\(\sqrt{4}\)は\(2\)であり、また\(-2\)でもあるのです。
\(\sqrt{\,\,\,\,\,}\)を多価関数であると考えると\(-2\)の不公平感は全くなくなったわけですが、普通の関数に慣れ親しんでいる私たちにとって、同じ値を入れて2つの値が出てくるというのはとても気持ち悪く感じます。たかが「\(-2\)がかわいそう」という理由だけでこのような多価関数という概念を許してしまってよいものでしょうか?
このような気持ち悪さを解消するために、複素関数論で多くの業績を残したリーマンはリーマン面という概念を考えました。
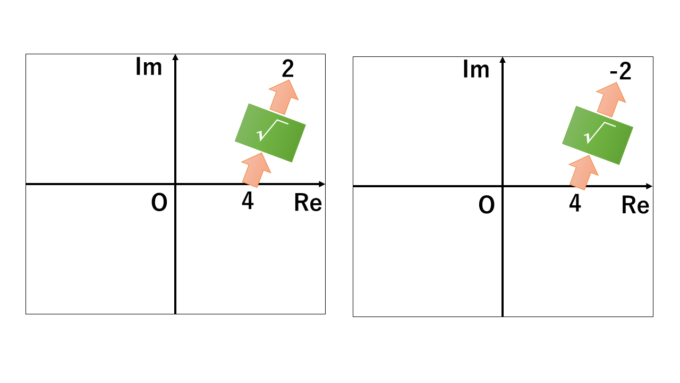
まず、2つの複素平面を用意します。そして、\(\sqrt{\,\,\,\,\,}\)はこの2枚の複素平面上で定義されていると関数とみなすのです。つまり同じ\(4\)でも左の複素平面上の\(4\)と、右の複素平面上の\(4\)では異なるものと考え、\(\sqrt{\,\,\,\,\,}\)に左の\(4\)を入れると\(2\)が、右の\(4\)を入れると\(-2\)が出てくると考えるのです。
そして、リーマンはこの2枚の複素平面のそれぞれで実軸の負の部分に切れ込みを入れ、図のようにピンク色の部分同士、水色の部分同士をつなげました。
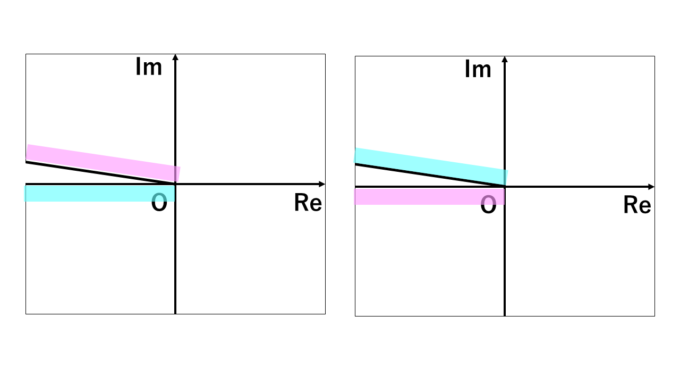
つまり、左の複素平面で実軸の負の部分の上方から赤矢印に沿って点を動かしていくと、右の複素平面の実軸の負の部分の下方から出てくるのです。青い矢印、緑の矢印も見ていただければイメージできるかと思います。
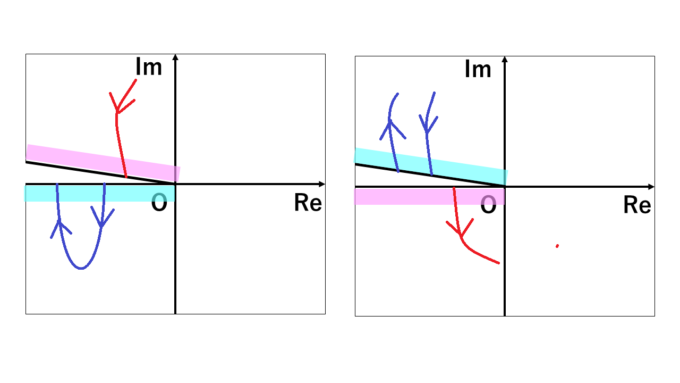
2枚の複素平面をこのようにつなげたものを、\(\sqrt{\,\,\,\,\,}\)のリーマン面と呼びます。
リーマン面を用いて\(\sqrt{4}=-2\)を実感する
\(\sqrt{\,\,\,\,\,}\)のリーマン面を認めた上で\(\sqrt{4}=-2\)を実感してみましょう。なんとエクセルで簡単に実感できます。
中学校で習った\(\sqrt{4}=2\)を出発地点として\(\sqrt{4}=-2\)を実感しましょう。出発地点では\(\sqrt{\,\,\,\,\,}\)の中に\(4\)を入れていますが、複素平面上の曲線を旅路にして、\(\sqrt{\,\,\,\,\,}\)の中に入れる\(4\)を少しずつ変えていきます。例えば、以下の赤、青、緑、黄の曲線を旅路にしてみましょう。
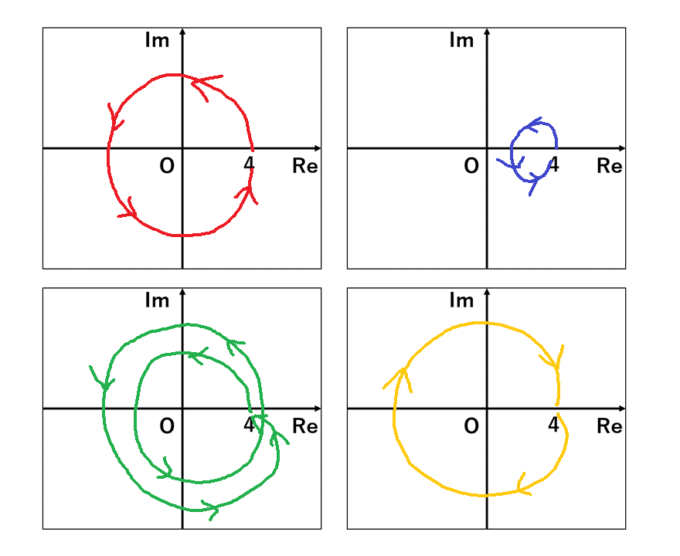
しかし、\(\sqrt{\,\,\,\,\,}\)は多価関数です、出発地点の\(\sqrt{4}\)は\(2\)と定めたとして、そこからちょっとでもずれた点、例えば\(4+0.1i\)の点で\(\sqrt{4+0.1i}\)は\(2.0001+0.02499i\)と\(-2.0001-0.02499i\) という2つの出力のうちどちらを選べばよいでしょうか?
この疑問に答えるために、\(\sqrt{\,\,\,\,\,}\)という関数の連続性に注目します。\(\sqrt{\,\,\,\,\,}\)の中に入れた\(4+0.1i\)は\(4\)からちょっとしか動いていません。そのため出力も\(2\)からちょっとしか動いていないと考えるのです。\(2.0001+0.02499i\)と\(-2.0001-0.02499i\)であれば\(2.0001+0.02499i\)の方が\(2\)に近いので、出発直後の\(\sqrt{4+0.1i}\)では\(2.0001+0.02499i\)の値をとると考えます。このように赤、青、緑、黄の曲線に沿って歩きながら\(\sqrt{\,\,\,\,\,}\)の中に複素数を入れていくのですが、その時の出力は一歩前の出力に近いほうを選ぶというルールにすることで出力を一つに決めることができます。
赤、青、緑、黄の曲線は\(4\)から出発して最終的に\(4\)に戻ってきています。ゴール地点の\(4\)で\(\sqrt{\,\,\,\,\,}\)が取る値を計算できるので、これで\(-2\)が出てきたら\(\sqrt{4}=-2\)が実感できたことになります。
この4本の曲線のうち、ゴール地点の\(4\)で\(\sqrt{4}=-2\)となるのはどれだと思いますか?リーマン面を意識して、考えてみてください。
エクセルで実験
それでは実際にエクセルで計算してみます。赤、緑、青、黄の曲線のパラメータを\(t\)として入力\(z(t)\)、出力\(w(t)\)の実部、虚部をそれぞれ計算していきます。特に出力はIF関数を用いて\(\sqrt{\,\,\,\,\,}\)の2つの出力のうち一歩前の出力に近い方を選んでいます。記事の中では詳しく紹介しませんが、記事最後に簡単な動画で解説しておりますので、エクセルを使った実験に興味がある方はそちらをご覧ください。
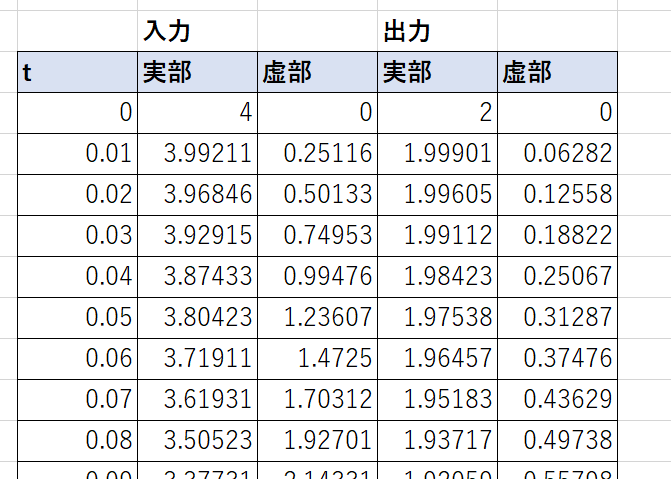
そして、実際に計算してみると!!
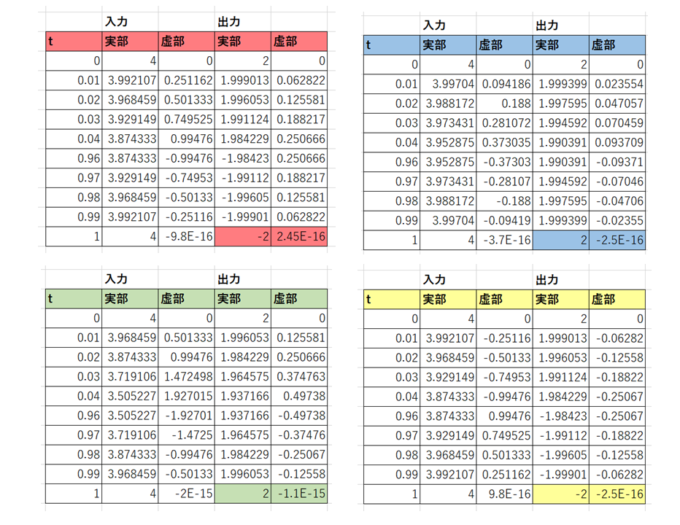
上のような結果になりました。赤と黄の曲線を旅路にするとゴール地点で\(\sqrt{4}=-2\)になっています。また残念ながら青、緑の曲線のゴール地点では\(\sqrt{4}=2\)になります。
これはリーマン面上でそれぞれの道を図示したら納得がいきます。
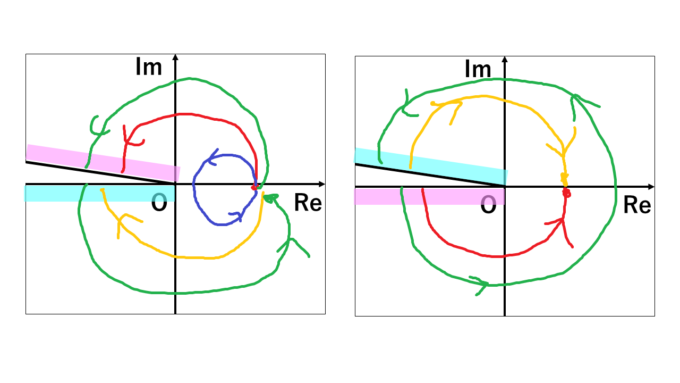
赤、青、緑、黄といずれも左の複素平面上の\(4\)から出発していますが、赤と黄の曲線に関してはゴール地点が右の複素平面上の\(4\)になっていることが分かります。また青と緑の曲線のゴール地点は左の複素平面上の\(4\)になっています。
エクセルを使ってこんなにお手軽に\(\sqrt{4}=-2\)が実感できるなんてとても面白いですね。
(文/松中)













