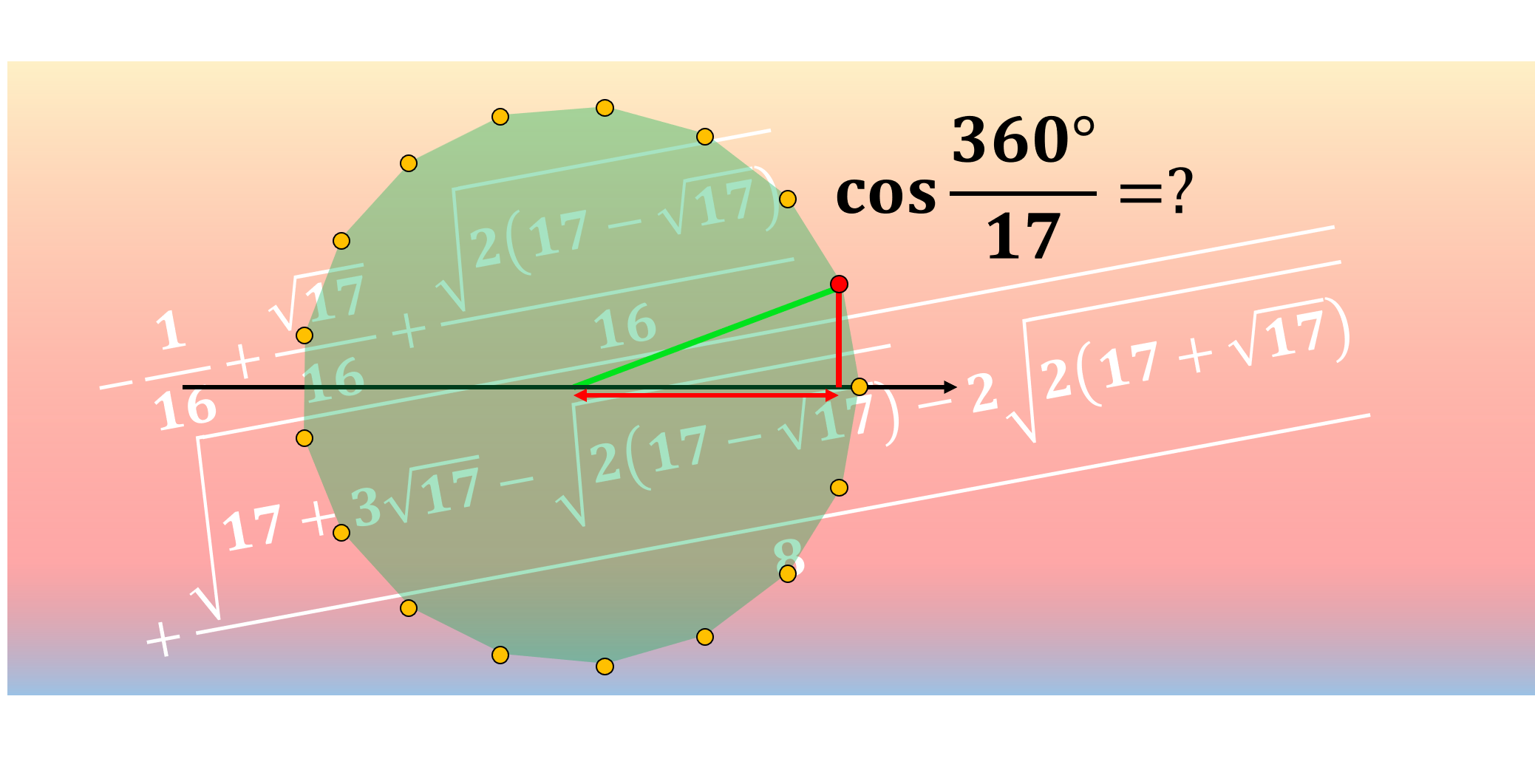
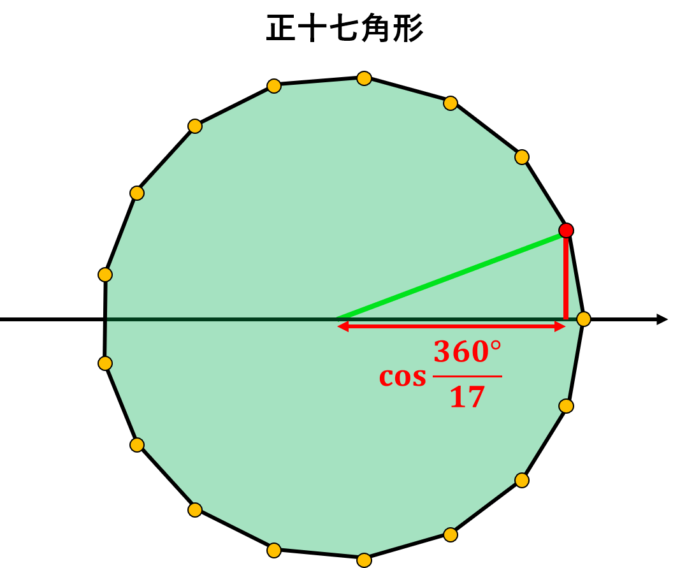
みなさんこんにちは！和からの数学講師の岡本です。今日はひょんなことから$\cos(2\pi/17)$の値を求めてみたくなったので解説していきます。そもそも$\cos(2\pi/17)$とは、下図のように単位円に内接する正十七角形における赤い点の$x$座標の値です。この値がどのようにして求められるかに非常に興味があります。

１．準備

最初に$\cos(2\pi/17)$を求めるのに必要な基本公式をまとめていきます。特に問題ない方は読み飛ばしていただいても構いません。まずは三角関数の加法定理からただちに得られる積和の公式です。

$$\begin{align*} \cos\theta_1\cos\theta_2=\frac{1}{2}\{\cos(\theta_1-\theta_2)+\cos(\theta_1+\theta_2)\}. \end{align*}$$

この公式はやたらと使うので確認しておきましょう。次に$\cos$の対称性です。$0\leq\theta\leq2\pi$に対して以下が成り立ちます。

$$\begin{align*} \cos(2\pi-\theta)=\cos\theta. \end{align*}$$

そして、$\cos$に関する次のシンプルな公式（以降、「$\cos$の和の公式」と呼ぶことにします。）も使います。$\theta=2\pi/n$としたとき

$$\begin{align*} \cos\theta+\cos2\theta+\cdots+\cos (n-1)\theta=\sum_{k=1}^{n-1}\cos k\theta=-1 \end{align*}$$

が成り立ちます。これは複素数$z=e^{i\theta}=\cos\theta+i\sin\theta$とすると、ド・モアブルの定理により$z^k=\cos k\theta+i\sin k\theta$であり、また、$\theta=2\pi/n$であることから$z^n=1$となります。したがって

$$\begin{align*} 1+\sum_{k=1}^{n-1}\cos k\theta+i\sum_{k=1}^{n-1}\sin k\theta=1+z+z^2+\cdots+z^{n-1}=1+\sum_{k=1}^{n-1}z^k=\frac{1-z^n}{1-z}=0 \end{align*}$$

となり、実部のみに注目すると

$$\begin{align*} 1+\sum_{k=1}^{n-1}\cos k\theta=0 \end{align*}$$

であることから$\cos$の和の等式が導けました。次に2次方程式の解の公式についても確認しておきましょう。2次方程式$ax^2+bx+c=0$を満たす解は

$$\begin{align*} x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{align*}$$

となります。さらに、実数$\alpha, \beta$が$\alpha+\beta=p, \alpha\beta=q$を満たすとき、$\alpha,\beta$は次の2次方程式

$$\begin{align*} x^2-px+q=0 \end{align*}$$

の解と考えることができる点も抑えておきましょう。

２．$\cos(2\pi/17)$を求める（第1段階）

毎回$\cos(2\pi/17)$と書くのは面倒なので、$\theta=2\pi/17$とおいておきます。つまり、いまから$\cos\theta$を求めることが目的となります。さて、そんなことはさておき、突然ですが次のような$\cos$たちの和を考えましょう。

$$\begin{align*} a_1&=\cos\theta+\cos4\theta\\ a_2&=\cos2\theta+\cos8\theta\\ b_1&=\cos3\theta+\cos5\theta\\ b_2&=\cos6\theta+\cos7\theta \end{align*}$$

ここで、$A:=a_1+a_2, B:=b_1+b_2$とおきます。まず、$A+B=\cos\theta+\cdots+\cos8\theta$の値を求めます。そこで$\cos$の和の公式より

$$\begin{align*} \sum_{k=1}^{16}\cos k\theta=\sum_{k=1}^{8}\cos k\theta+\sum_{k=9}^{16}\cos(2\pi-k\theta)=2\sum_{k=1}^{8}\cos k\theta=-1 \end{align*}$$

であることから$A+B=-1/2$であることがわかります。次に$AB$の値を求めます。$AB$の値が分かれば、$A,B$は2次方程式の解としてそれぞれ求めることができます。これが第1段階です。第2段階は$a_1+a_2, a_1a_2$の値から2次方程式の解として$a_1, a_2$を求めます。これを繰り返していけば$\cos\theta$の値を求めることができるという寸法です！

さて、$AB=(a_1+a_2)(b_1+b_2)=a_1b_1+a_1b_2+a_2b_1+a_2b_2$なので、それぞれの項$a_ib_j$を求めていくことにしましょう。計算には積和の公式を使います。

$$\begin{align*} a_1b_1&=(\cos\theta+\cos4\theta)(\cos3\theta+\theta5\theta)\\ &=\cos\theta\cos3\theta+\cos\theta\cos5\theta+\cos4\theta\cos3\theta+\cos4\theta\cos5\theta\\ &=\frac{1}{2}(\cos2\theta+\cos4\theta+\cos4\theta+\cos6\theta+\cos\theta+\cos7\theta+\cos\theta+\cos9\theta)\\ &=\frac{1}{2}(2a_1+a_2+b_2) \end{align*}$$

他の項も同様に計算してまとめると

$$\begin{align*} a_1b_1&=\frac{1}{2}(2a_1+a_2+b_2)\\ a_1b_2&=\frac{1}{2}(a_2+b_1+2b_2)\\ a_2b_1&=\frac{1}{2}(a_1+2b_1+b_2)\\ a_2b_2&=\frac{1}{2}(a_1+2a_2+b_1)\\ \end{align*}$$

となり、$AB$は

$$\begin{align*} AB=\frac{1}{2}(4a_1+4a_2+4b_1+4b_2)=2(A+B)=-1 \end{align*}$$

と求められます（とても綺麗ですね）。したがって、$A,B$は2次方程式$x^2+(1/2)x-1=0$の解であり、その実数解は$\frac{-1\pm\sqrt{17}}{4}$であることがわかります。なお、$A>0,B<0$であることから、$A=\frac{-1+\sqrt{17}}{4}, B=\frac{-1-\sqrt{17}}{4}$となります。（$A,B$の正負は角度の情報からわかりますが、少々面倒なので、今回は省略します）

３．$\cos(2\pi/17)$を求める（第2段階）

$a_1+a_2=A$の値が分かったので、次に$a_1a_2$の値を求めます。先ほどと同様に積和の公式を用いて計算すると

$$\begin{align*} a_1a_2&=(\cos\theta+\cos4\theta)(\cos2\theta+\cos8\theta)\\ &=\cos\theta\cos2\theta+\cos\theta\cos8\theta+\cos4\theta\cos2\theta+\cos4\theta\cos8\theta\\ &=\frac{1}{2}(\cos\theta+\cos3\theta+\cos7\theta+\cos9\theta+\cos2\theta+\cos6\theta+\cos4\theta+\cos12\theta)\\ &=\frac{1}{2}(\cos\theta+\cos2\theta+\cdots+\cos8\theta)\\ &=-\frac{1}{4} \end{align*}$$

となり、$a_1, a_2$は2次方程式$x^2-Ax-1/4=0$の解であることがわかります。$a_1>0, a_2<0$であることから（これも角度の情報からわかりますが、面倒なので省略します）、

$$\begin{align*} a_1=\frac{A+\sqrt{A^2+1}}{2}=\frac{-1+\sqrt{17}+\sqrt{2(17-\sqrt{17})}}{8} \end{align*}$$

であることがわかりました。

４．$\cos(2\pi/17)$を求める（最終段階）

ここまでで$a_1=\cos\theta+\cos4\theta$の値を求めることができました。最後に$\cos\theta\cos4\theta$の値を求めていきます。積和の公式より

$$\begin{align*} \cos\theta\cos4\theta=\frac{1}{2}(\cos3\theta+\cos5\theta)=\frac{1}{2}b_1 \end{align*}$$

となり、$b_1$を求めればよいことがわかりました。$b_1+b_2=B$の値は第1段階で既に計算済みであり、$b_1b_2$の値は$a_1a_2$と同様に計算すると$-1/4$であることがわかります。したがって2次方程式$x^2-Bx-1/4$の解として$b_1, b_2$を求めることができます。結果として

$$\begin{align*} b_1=\frac{B+\sqrt{B^2+1}}{2}=\frac{-1-\sqrt{17}+\sqrt{2(17+\sqrt{17})}}{8} \end{align*}$$

となります。よって、$\cos\theta, \cos4\theta$は2次方程式$x^2-a_1x+1/2b_1$の解であり、$\cos\theta>\cos4\theta$より

と求めることができました。

５．さいごに

ここまで、$\cos(2\pi/17)$を求めるのに様々な計算を行ってきましたが、結果的に2次方程式を繰り返し解く形で値が求められました。つまり、四則演算（足し算、引き算、掛け算、割り算）と平方根（ルート）の計算だけで$\cos(2\pi/17)$を得られたわけです。実は、与えられた長さに対して四則演算やルート計算を施して得られる長さはコンパスと定規のみで作図できることが知られています！したがって、正十七角形はコンパスと定規のみで作図可能であるということが最後の$\cos(2\pi/17)$の式の形からただちに導けます！なお、どんな3以上の自然数$n$に対しても$\cos(2\pi/n)$の値は四則演算と平方根で表せるとは限りません。つまり、正多角形には作図可能なものとそうでないものがあるわけです！こうした作図可能性を、代数学の「体の2次拡大」の理論というもので特徴付けることができます（実際に作図可能な自然数$n$の必要純分条件も求められています）！作図という、一見素朴な話題ですが、実は非常にロマンティックなのです！

コンパスと定規の作図に関する話題は瀬山士郎先生の本がオススメです。

コンパスと定規の幾何学　瀬山 士郎 (著)他　共立出版

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>