みなさんこんにちは。和からの数学講師の伊藤です。前回の記事では、対象を1列に並べる順列の考え方をご紹介しましたが、今回は対象の中から複数を選択する組み合わせの考え方を見ていきます。前回の順列でご紹介した「！」（階乗記号）も使用しますので、必要に応じてこちらもご確認ください！

【前回記事のURL】

１. 組み合わせ

今回は、次のような問題を考えましょう。

前回の➁の問題「生徒会員5人の中から会長、副会長、書記を選出する。選出の仕方は何通り？」と似ていますが、今回は3人の中に役割関係は特になく、役員を選択するだけでよい状況です。したがって生徒を並べるという考え方よりも、生徒の組み合わせ方が何通りあるかを計算することになります。

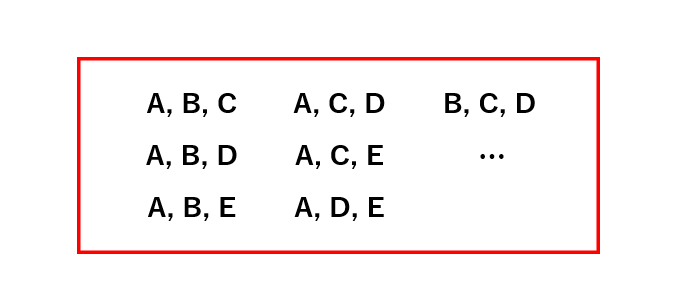
このように、異なるn個の物からm個の組み合わせを選ぶという選び方を、組み合わせと言います。

２. 組み合わせを使った場合の数の計算

前回、5人の生徒会員から会長、副会長、書記を選出する場合、120通りの選び方があることが分かりました。生徒をA, B, C, D, Eとするとき、選び方は次のようになっています。

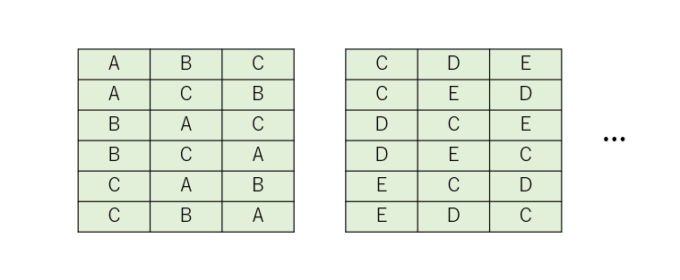
ここで注目したいのは、順列の場合は会長、副会長、書記にA, B, Cを選出する場合とB, A, Cを選出する場合とを区別していた点です。このように3人を順に並べる並べ方は全部で\(3!=6\)通りありますが、今回は3人の執行役を選出するだけでよいので、この役割の違いは全て無視できることになります。したがって、組み合わせの場合は以下のような数え方をしていきます。

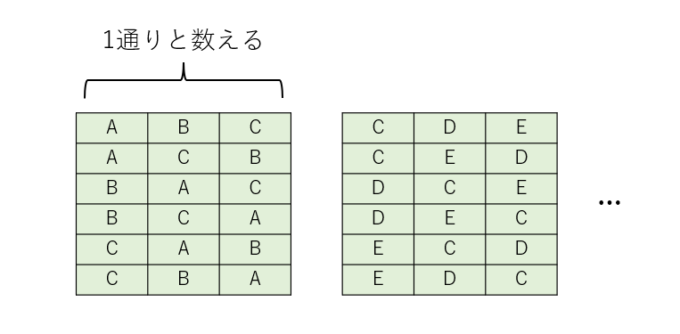
この関係から、5人のうちから会長、副会長、書記を選出する場合の数は、5人のうちから3人の組み合わせを選出する場合の数を\(3!\)倍すれば良いことになります。

以上から、n人の中からm人を選出する組み合わせの総数は、\({}_nP_m\)の値を\(m!\)で割ることで求められます。

３. 組み合わせの表し方

n人の生徒からm人を選ぶ組み合わせの総数を上記の方法で計算する場合、記号「C」を用いて以下のように表現します。

\begin{align*}
{}_n C_m = \frac{{}_nP_m}{m!}
\end{align*}

記号「C」は、組み合わせ（Combination）の頭文字から来ており、n人の生徒の中からm人を選ぶ組み合わせの総数を意味します。5人の生徒から3人を選ぶ場合、\({}_5C_3= ( 5 \times 4 \times 3 ) / 3! = 10 \)という計算になります。

組み合わせ記号Cは、場合の数の計算以外にも、式の展開など数学の各場面で必要になります。記号の意味と計算方法をマスターして、いろいろな計算に活かしていきましょう！

●和からのセミナー案内

Excelを用いたデータ分析のストーリーや可視化のスキルを学んでいくセミナーのご紹介です。興味を持っていただけた方は、ぜひ覗いてみてください！

初めて学ぶデータ利活用-Excel編-

Excelで学ぶ統計グラフの世界-データのビジュアル化-

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/伊藤智也>

数学ガールの秘密ノート/確率の冒険 結城 浩(著) SBクリエイティブ