やさしく学ぶ統計学～順列とは～

統計・機械学習トピック

公開日

2023年3月16日

更新日

2023年3月16日

みなさんこんにちは。和からの数学講師の伊藤です。今回は、場合の数や確率を考える際に必要な概念となる順列について見ていきましょう。具体的な例を用いて順列の意味や使い方を覚えていただけますと幸いです！

この記事の主な内容

１. 順列

今回は、次のような問題を考えましょう。

➀5つの椅子が1列に並んでおり、5人の生徒を座らせる。座り方は何通り？
➁生徒会員5人の中から会長、副会長、書記を選出する。選出の仕方は何通り？

➀の問題と➁の問題は一見違ったタイプの問題に見えますが、共通した考え方で捉えることができます。それが、異なるものを一列に並べるということです。➁の問題に関しては「1列に並べる」というイメージがしづらいかもしれませんが、5人の生徒から3人選び、先頭から順に会長、副会長、書記に選出するように並べるという見方をすることができます。

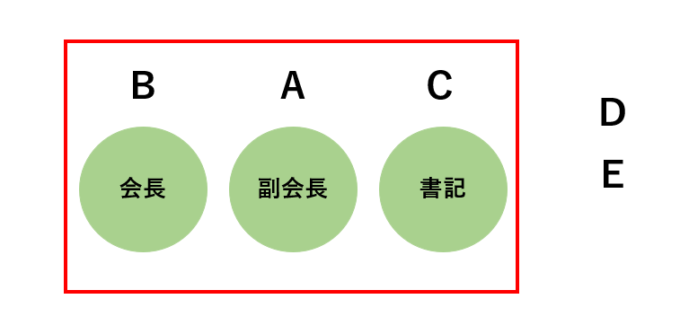
このように、異なるn個のものを1列に並べるという並べ方を、順列と呼びます。

２. 順列を使った場合の数の計算

順列の考え方を使って、先ほどの問題➀、➁を考えていきましょう。まずは問題➀です。

5つの椅子に5人の生徒が座る場合、先頭の椅子に座る生徒は5通り考えられます。また、それぞれの場合において、2番目の椅子に座る生徒は先頭の1人以外の生徒が考えられるので、4通りの座り方があります。同様の考え方から、3番目の椅子に座る生徒が3通り、4番目の椅子に座る生徒が2通りとなり、最後尾の椅子に座る生徒はこの時点で自動的に決定します。

以上をまとめて、5人の生徒を1列に並べる並べ方が、5×4×3×2×1=120通り存在することが分かります。

では、➁の問題も同様に考えていきましょう。この場合は、5人の生徒のうち3人を椅子に座らせ、先頭から会長、副会長、書記と任命する形で考えます。先頭に座る生徒の選び方が5通りあり、次の椅子に座る生徒の選び方が4通り、さらに次の椅子に座る座り方が3通りとなります。よって、今回は5×4×3=60通りが答えとなります。

３. 順列の表し方

以上のように、n人の生徒を1列に並べる、もしくはn人の生徒からm人選んで1列に並べる場合の数は、数字を順に掛け算していく方法で計算することができます。この場合、記号「P」を用いて以下のように表現します。

\begin{align*}
{}_n P_m = n \times (n-1) \times \cdots \times ( n-m+1)
\end{align*}

記号「P」は、順列（Permutation）の頭文字から来ています。この計算は、n人の生徒の中からm人を選び、1列に並べる場合の数を意味します。今回の➁の問題の場合、5人の生徒から3人を選んで1列に並べるという見方ができるので、\({}_5 P_3=5 \times 4 \times 3\)という計算となります。

また、nとmが一致する状況は、「！」記号を用いて表現します。つまり

\begin{align*}
n!=n \times (n-1) \times \cdots \times 1
\end{align*}

となります。「！」は階乗記号と呼び、各分野で目にする機会もあるかと思います。これらの記号の使い方はぜひ覚えておきましょう！