みなさんこんにちは！和からの数学講師の岡本です。以前、授業の中で「2次関数と図形」に関する話題を扱いました。その際に例題として作成した問題が思いのほか面白い問題だったのでご紹介したいと思います。

１．2次関数と平行四辺形の問題

では早速ですが、考えたい問題はこちらです。

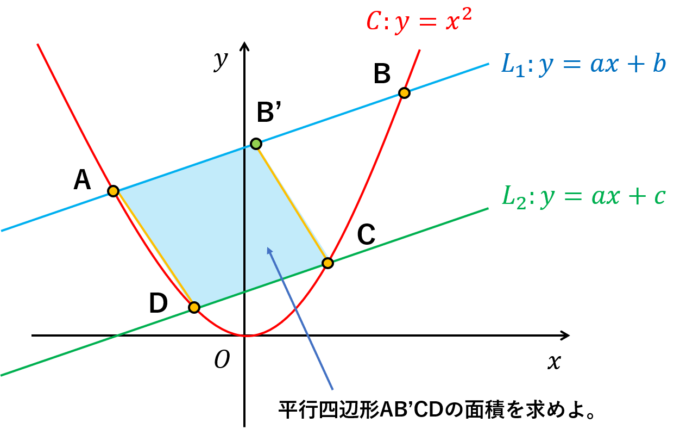
コテコテの2次関数の問題で、高校1年生程度の数学（数学Ⅰの範囲）の知識で解けると思います。今回はこの問題の様々な解法を紹介しようと思います。

２．CDの長さを求める

平行四辺形の面積は(底辺)×(高さ)で求められます。そこで、底辺であるCDの長さ\(l\)と、２つの平行線の距離\(d\)を求めることが最初の目標になります。

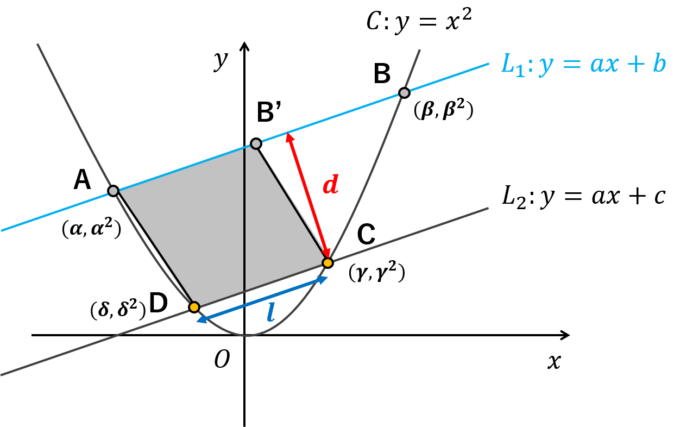
まずはA,B,C,Dの\(x\)座標をそれぞれ\(\alpha, \beta, \gamma, \delta\)とおきましょう。このとき、Cの座標は\(\gamma, \gamma^2\)と表せますが、直線\(L_2\)上の点でもあるので\((\gamma,a\gamma+c)\)とも表現できることに注意しましょう。Dも同様に考えてCDの長さ\(l\)は点同士の距離の公式（三平方の定理）により

\begin{align*}
l=\sqrt{(\gamma-\delta)^2+(a\gamma+c-(a\delta+c))^2}=(\gamma-\delta)\sqrt{a^2+1}
\end{align*}

と求めることができます。また、\(\gamma,\delta\)は2次方程式\(x^2-ax-c=0\)の異なる2つの実数解と考えることができるので、2次方程式の解の公式により

\begin{align*}
\gamma=\frac{a+\sqrt{a^2+4c}}{2}, \delta=\frac{a-\sqrt{a^2+4c}}{2}
\end{align*}

と、具体的に求められ、\(\gamma-\delta=\sqrt{a^2+4c}\)であることがわかります。したがって、CDの長さは\(\sqrt{(a^2+1)(a^2+4c)}\)であることがわかりました。

３．２つの平行な直線の距離を求める

次に、２つの直線の距離\(d\)を求めます。これは、「点Cと直線\(L_1\)との距離」と考えることができ、点と直線の距離の公式が利用できます。これにより、\(d\)は

\begin{align*}
d=\frac{|a\gamma-(a\gamma+c)+b|}{\sqrt{a^2+1}}=\frac{b-c}{\sqrt{a^2+1}}
\end{align*}

と計算することができます。これにより平行四辺形AB’CDの面積\(S\)は

\begin{align*}
l\times d=\sqrt{(a^2+1)(a^2+4c)}\times \frac{b-c}{\sqrt{a^2+1}}=(b-c)\sqrt{a^2+4c}
\end{align*}

であることがわかりました。

４．さいごに

いかがでしたでしょうか？今回は平行四辺形の性質を使い、点と点の距離、点と直線の距離の公式と2次方程式の解の公式をうまく利用することで、求めたい面積を\(a,b,c\)だけで表すことができました。しかし、面積を求める方法はこれだけではありません！次回は今回ご紹介した以外の方法を使って面積を求めていきたいと思います。お楽しみに！

高校数学の学び直しはこちら長岡先生の本がオススメです！

長岡先生の授業が聞ける高校数学の教科書（音声ＤＬ付） Kindle版　旺文社

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>