日常生活やビジネスにも使える!?「概算力」を鍛えよう!
公開日
2021年12月15日
更新日
2021年12月15日
動画で見たい方はこちら↓↓↓
こんにちは。和からの数学講師の岡本です。今回は「概算」についてお話していきたいと思います。「概算」とは「厳密でなく、大まかな見積り」のことを指します。小学校の算数でも「四捨五入」という概念が登場します。これも概算の一種です。こうした大まかな数字に読み取りはお仕事でも、もちろん日常生活でも大いに役に立ちます。
この記事の主な内容
1.資料からおおよその割合(パーセント)を読み取ってみよう
以前データ分析の授業をしているときに、ヒストグラムを読み取る問題がでてきました。それは、「都道府県庁所在市別の2人以上の世帯における平均年齢が60歳以上である地域は全体の何パーセントでしょう?」という問題です。
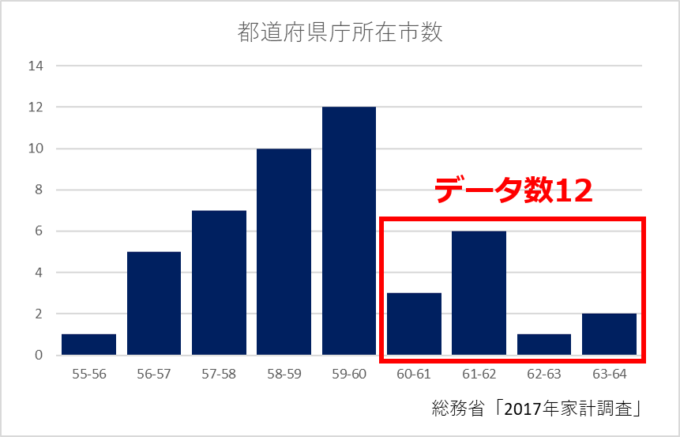
図からわかるように、60歳以上の地域の数は12個なので、単純に\(12/47\)という割合になります。重要なのはこれからで、これがおよそ何パーセントぐらいなのかを考えてみましょう。
2.概算のポイントその1
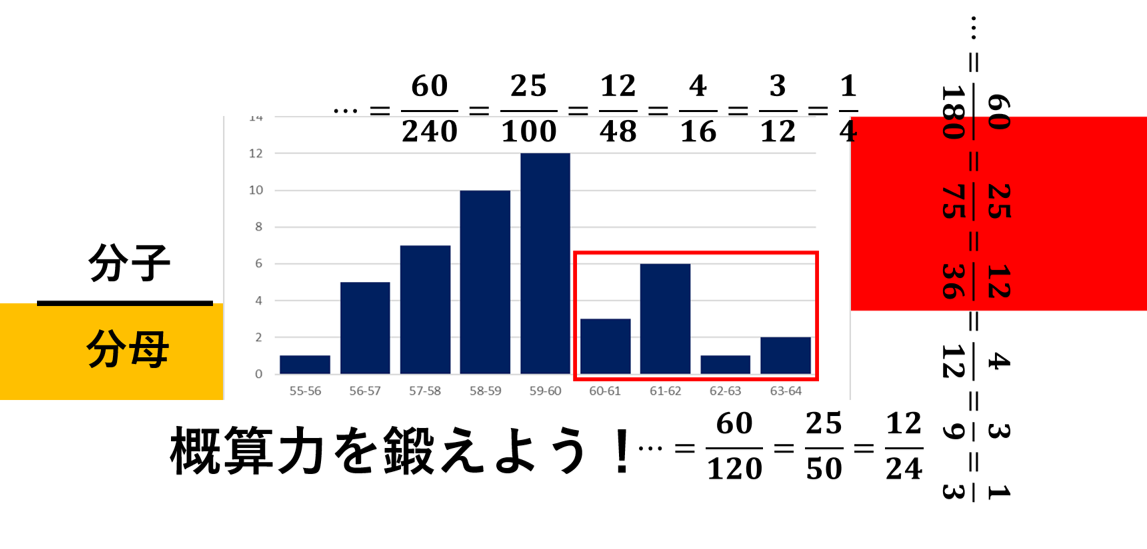
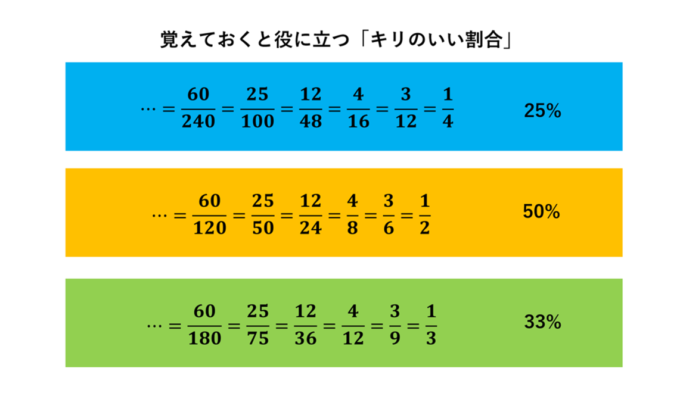
この問題における最初のポイントは「47」を「48」に変えてみることです。48はちょうど12の4倍なので、\(\frac{12}{48}=\frac{1}{4}\)、つまり、\(\frac{12}{47}\)は「およそ25%」であることがわかります!このように、約分しやすい数字組み合わせ(キリのいい割合)をいくつか押さえておくことで、数字の概算はスムーズに行えます。
3.概算のポイントその2
場合によっては、「\(\frac{12}{47}\)は約25%」という認識では十分でないことがあります。例えばもう少し正確に、「25%より大きいのか?小さいのか?」ということが知りたい場合などです。こうした場合は分数の性質をしっかりおさえておく必要があります。

分数は「分母」と「分子」に分かれていて、下が「分母」で上が「分子」です。ちょうど「お母さんが子どもをおんぶしている」イメージです。そして、分子が大きくなれば分数の値は大きくなり、分子が小さければもちろん小さくなります。重要なのは、「分母が大きくなるとき、分数が小さくなり、分母が小さくなるとき、分数が大きくなる」という点です。これが分数ならではの大切な性質です。今更あたりまえじゃないかと思われますが、概算で大いに役に立ちます。
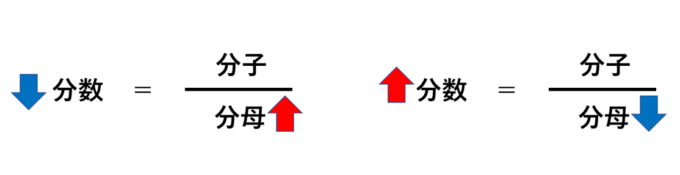
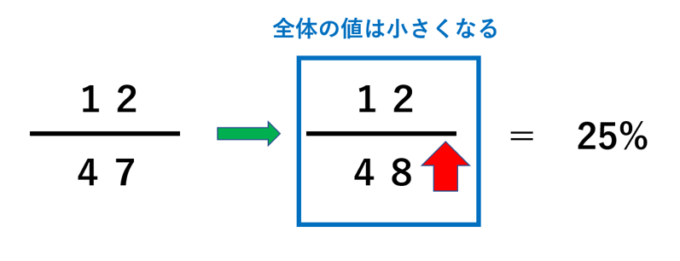
例えば、先ほどの\(\frac{12}{47}\)の例を考えてみましょう。「概算のポイントその1」でお話したように、この分数はおよそ「\(\frac{12}{48}=25\)%」と考えることができます。このとき、分母の\(47\)を1大きくしています。つまり、分母が大きくなっているので、分数\(\frac{12}{47}\)の値よりも少し小さくなっているのです。そして、「少し小さくなった値が25%」であることから、元の\(\frac{12}{47}\)は「25%よりも少し大きい値」であることが予想できます。実際に計算してみると25.532%となるので、正しく概算ができています!
4.さいごに
いかがでしたでしょうか?日常でもよくみる「数字」の扱い方は整理の仕方や簡単な計算方法を知っているだけで、驚くほどスピーディにつかむことができます。特に近年では数字やデータから判断する機会が格段に増えてきました。和からではデータ分析とな何なのかや、簡単な数字の捉え方や集計の仕方に関する無料のセミナーを行っています。興味のある方は是非ご参加ください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>














