動画で見たい方はこちら↓↓↓

こんにちは。和からの数学講師の岡本です。今回は友人からプレゼントされた鉛筆についてのお話です。

１．数字が刻まれた鉛筆

　ある日、友人からイギリスのお土産をいただきました。中身は大量の鉛筆です！しかも、なにやら数字がたくさん書いてあります。

刻まれていたのは次のような数字の列でした。

\begin{align*}357686312646216567629137\end{align*}

一体どんな意味が隠されいるのでしょう…？

２．第一印象「きっと素数だ」

数字を見た素数好きの私は直感で「きっと素数だ」と思いました。そして、すかさず「素数チェッカ」という、（巷では有名な）素数判定アプリに入れて実行しました。すると…

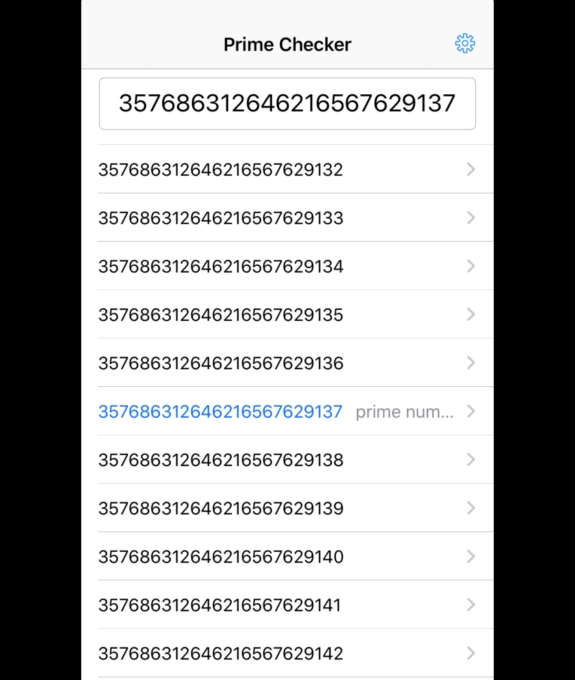
やはり素数だったのです…！（素数であれば数の隣に「prime number」と付きます。素数好きはみなここで興奮します。）しかし、どういう意味があるのでしょうか？イギリスの商品ですし、なにか数字の語呂があるわけでもなさそうです。そこで商品が「鉛筆」であることに注目して考えてみました。

「実際に鉛筆を使用すると、削れていくので、数字が変わっちゃうな…。」

ここでピンときました！

「も…、もしかして、削れてもずっと素数なんじゃ…！？」

恐る恐る、私は最初の数字を削った「\(57686312646216567629137\)」で素数判定をしてみました。すると…

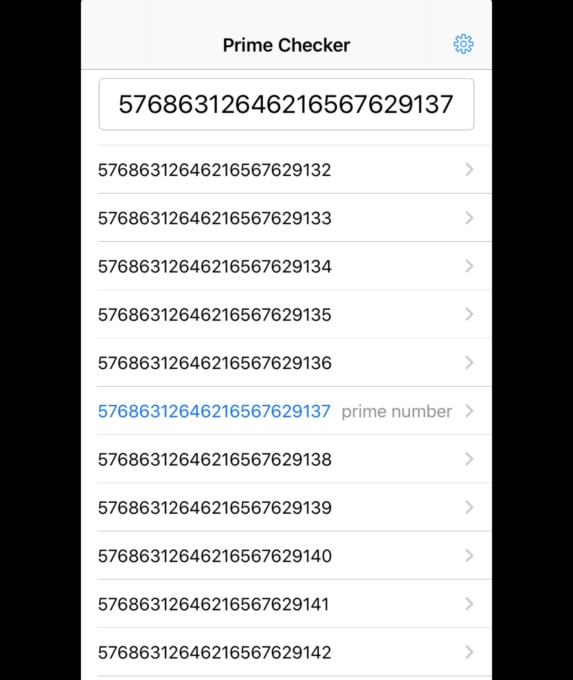
なんと、「\(57686312646216567629137\)」は素数です…！！
ではさらに「5」を削った「\(7686312646216567629137\)」はどうでしょう？

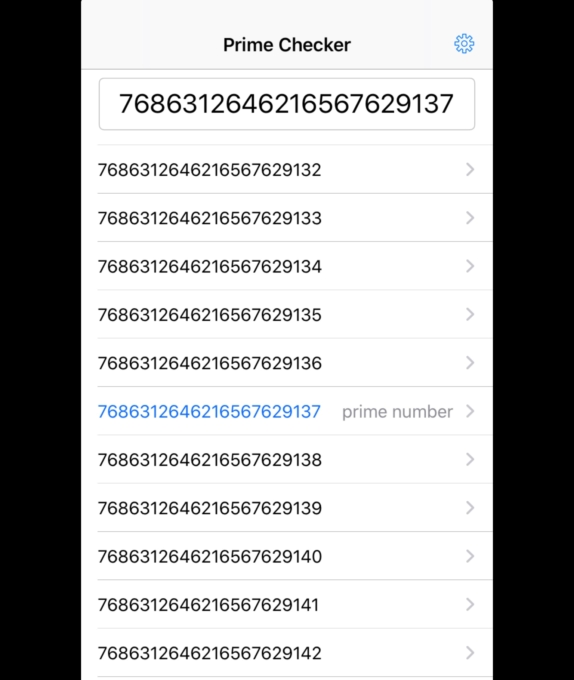
素数です！！！続きをやった結果がこちらです。

なんと鉛筆に書かれた「357686312646216567629137」は、「どんなに削られてもずっと素数」であるような素敵な素数だったのです！！！！

３．切り捨て可能素数

前節でお話したような「どんなに削られてもずっと素数」であり続けるような素数のことを切り捨て可能素数」といいます。ただし、今回が左の数を削っていることから正確には「左切り捨て可能素数」と言います。実は「357686312646216567629137」は最大の左切り捨て可能素数であることが知られています。もちろん「右切り捨て可能素数」もありますが、数字は左から右に読むので、数字の最後に「0,2,4,6,8」などの偶数があっては素数にならないので、「左切り捨て可能素数」の方がバリエーションが豊富そうです。探し方は非常にシンプルで、「1,3,7,9」の数字からスタートさせ、左に数字を付けていき素数かどうかを判定します。例えば、「9」から始めた場合を３桁目までまとめてみました。

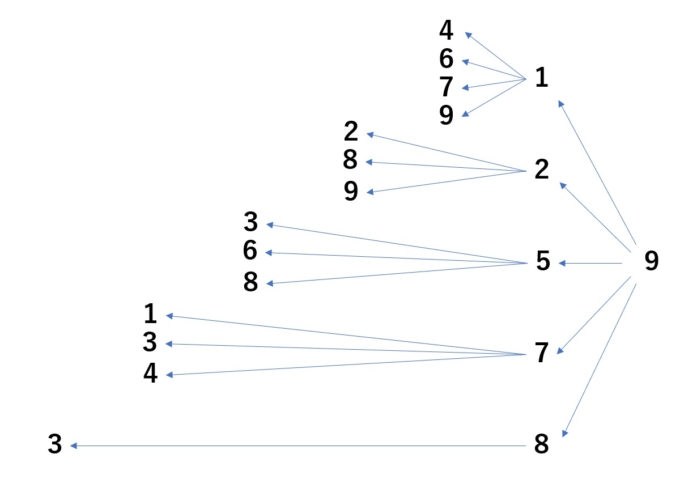
１桁目が9であるような２桁の素数は「19」「29」「59」「79」「89」の５つなので、最初の9から左に５本矢印が伸びます。そして下２桁が19であるような３桁の素数は「419」「619」「719」「919」の４通りあるためまた左に矢印が４本伸びます。このような操作を繰り返していくことで、左切り捨て可能素数が次々と出来上がります。そしてしらみつぶしに素数を作り出していくことで「357686312646216567629137」が最大の桁数になる左切り捨て可能素数ということがわかります。

４．さいごに

いかがでしたでしょうか。普段なかなか聞くことのないマニアックな「切り捨て可能素数」。使用するたびに削られる「鉛筆」にデザインされているのがユーモアがあっていいですのね。よくみると「ALWAYS IN OUR PRIME」（いつも私たちの素数の中に）と書いてあります

何事も楽しんで学ぶ、応用する、活用するというのがいいのだと思います。和からでは数学を用いた「デザイン」の無料セミナーも開催しております。興味のある方は是非！

数学的デザイン超入門

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>