※本記事はロマ数トレラン「楕円曲線論入門オンラインセミナー」の講師である木内敬先生による楕円曲線入門の記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。

楕円曲線とは

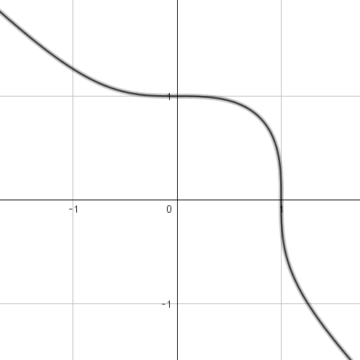
楕円曲線とは、$xy$平面上で3次多項式で表される図形や多項式自体を意味します。例えば、$x^3+y^3=1$（図1）や$y^2=x^3+1$（図2）は楕円曲線です。

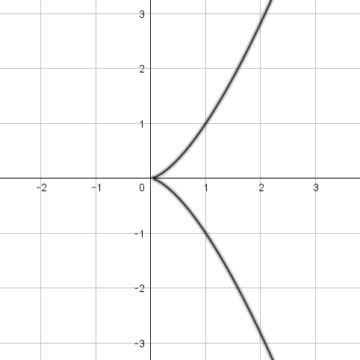
ただし、特異点をもつ場合は、楕円曲線に含めないことが多いです。特異点とは、接線を定めることができない点を言います。例えば、$y^2=x^3$（図3）は、原点で尖っているため原点での接線を定めることができません。また、$y^2=x(x-1)^2$は、$(1,0)$で交わっており（図4）、接線を定めることができませんので$(1,0)$は特異点となります。したがって、これらは、楕円曲線といいません。

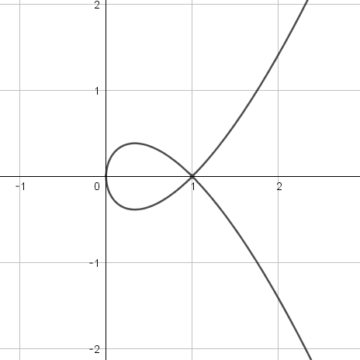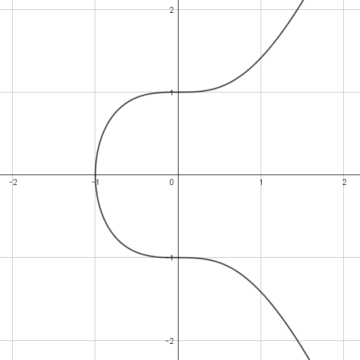
また、高校で習う3次曲線$y=x^3$（図5）は、各点で接線が引けますので、楕円曲線といえそうです。しかし実は、「特異点を持たない」という条件は、無限遠点においても「特異点を持たない」必要があります。このブログでは、無限遠点の定義には踏み込みませんが、実は、$y=x^3$は無限遠点で特異点となります。したがって、残念ながら$y=x^3$は楕円曲線とはいいません。

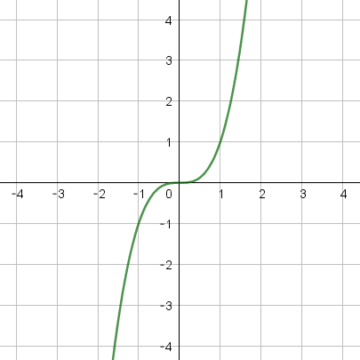
なぜ楕円曲線か

なぜ、楕円曲線を考えるのか。それは、一つには1次曲線、2次曲線についでやさしいものだからです。1次曲線はすなわち直線です。2次曲線は、放物線や楕円、双曲線です。これらは、中学、高校で習う通り、比較的やさしく描くことができ、その性質も明らかになっています。3次曲線である楕円曲線は、この次にやさしい曲線になります。

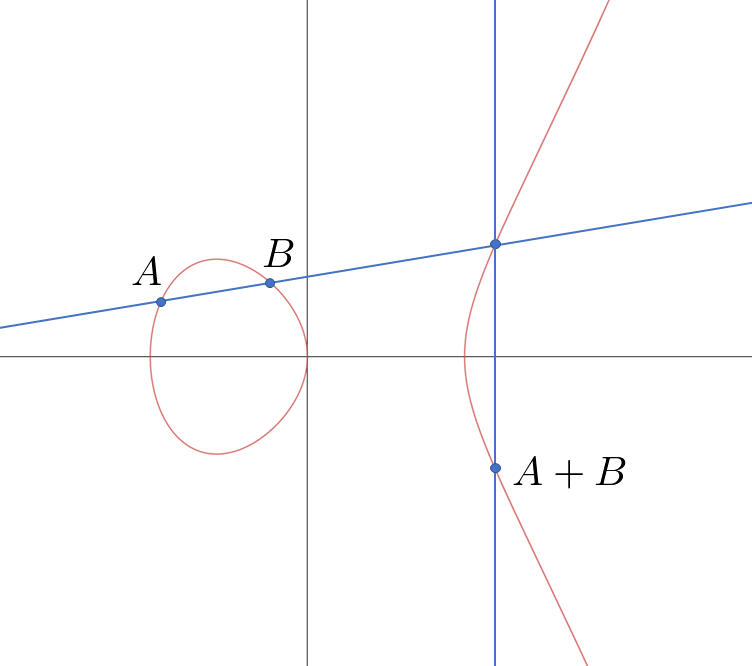
しかし、楕円曲線が重要なのはこれだけではありません。楕円曲線には、驚くべき性質があります。楕円曲線上の2点$P,Q$に対して、楕円曲線上の点$P+Q$が定義できるのです。ここでは、「＋」の記号を用いましたが、単なる座標の和ではありません。若干、複雑なので「＋」の定義は省略しますが、楕円曲線の各点はこの和を演算として「アーベル群」をなすのです。つまり、楕円曲線とは、単に1次曲線、2次曲線に次ぐ曲線というだけではなく、「アーベル群」という構造を有しており、このアーベル群という構造が楕円曲線を豊かなものしているために、現在でも活発に研究がなされているのです。

楕円曲線の有理点

楕円曲線のうち、有理数係数の楕円曲線を考えます。例えば、$x^3+y^3=1$は有理数係数ですが、$x^3+y^3=\sqrt{2}$は有理数係数ではありません。この、有理数係数の楕円曲線に対し、$x$座標、$ｙ$座標がともに有理数である楕円曲線上の点を「有理点」といい、$x$座標、$ｙ$座標ともに整数である楕円曲線上の点を「整点」といいます。当然ながら、整点は有理点でもあります。「整点」「有理点」を見つけることは整数論では重要な問題です。

フェルマーの大定理のうち3次のものは、$x^3+y^3=z^3$の自然数解は存在しないことを意味していますが、これを楕円曲線の言葉で表すと楕円曲線$x^3+y^3=1$が正の有理点がないことを意味しています。（仮に、正の有理点をもった場合には、共通分母を払うことにより、フェルマーの定理の反例が作れます。）

また、別の例になりますが、楕円曲線$x^3+y^3=1729$を考えます。$1729$は、タクシー数と呼ばれています。これは、入院中であったインドの鬼才ラマヌジャンを、師匠であるハーディーが見舞った際に、ハーディーはラマヌジャンに、「今乗ってきたタクシーのナンバーは$1729$だった。特に、これと言って面白い数ではない」といったところ、ラマヌジャンは即座に「$1729$は、二種類の方法で立方数の和として表すことができる最小の数です」と答えたことに由来します。つまり、$1729＝1^3+12^3=9^3+10^3$と二種類の方法で立方数の和として表すことができます。これを楕円曲線の言葉で表すと楕円曲線$x^3+y^3=1729$に、4つの整点$(x,y)= (1,12) (12,1),(9,10),(10,9)$があることを意味しています。

ここで問題となるのは、楕円曲線に有理点や整点は存在するのか？仮に存在するとして、どのくらい存在するのか？が問題となります。この有理点が整点が存在するのか？存在する場合にどの程度存在するのかということは、整数論の重要の問題ですが、なんと、上記で述べた楕円曲線のアーベル群の構造と関わっているのです。

楕円曲線のアーベル群の構造と有理点

楕円曲線はアーベル群の構造をもっています。したがって、何倍かしたら原点（ただし、この原点は、$xy$座標の原点ではなくアーベル群としての零点を意味しています。）に戻る点があります。この何倍かしたら原点に戻る点を有限位数の点といいます。この有限位数の点は、一般的に楕円曲線にはたくさんありますが、仮に有理点であった場合は、必ず整点になります（Nagell-Lutzの定理）。つまり、「有限位数の有理点は整点」になります。例えば、楕円曲線$x^3+y^3=1$の点で、3倍したら原点になる点は、$(1,0)$と$(0,1)$ですが、確かに整点となっています。このNagell-Lutzの定理の応用により、有限位数の有理点（この点は自動的に整点になります。）をすべて求めることができます。

また、楕円曲線上の有理点は、必ず、有限個の点の和で書くことができる、つまり、楕円曲線上の有理点は有限生成アーベル群であることが知られています（Mordellの定理）。例えば、楕円曲線$x^3+y^3=1729$上の有理点（この有理点は無限にあります。）は、ラマヌジャンが見つけた$(1,12)$と$(9,10)$で生成されることが示せます。ラマヌジャンが当時どこまで知っていたのかは分かりませんが、ラマヌジャンの発見した整数は、有限生成アーベル群の生成元だったのです。このように、楕円曲線の有理点や整点を見つけるということが、整数論の重要な問題であること、それを考える際に楕円曲線の群構造が重要になることが分かったかと思います。このほか、このブログには書ききれませんが、楕円曲線には、虚数乗法論や暗号理論との関係など汲めども尽きない話題が満載されています！

<文/木内敬>