トポロジー有名定理その２～ジョルダン・ブラウワーの分離定理～

おすすめイベント・ゼミ

公開日

2021年10月6日

更新日

2021年10月6日

※本記事はロマ数トレラン「微分トポロジー入門－境界付き多様体とmod 2交差理論－」の講師である佐々木和美先生によるトポロジーの有名定理の解説記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。

ロマ数トレラン「微分トポロジー入門－境界付き多様体とmod 2交差理論－」の詳細、お申し込みはこちらのページよりお願いいたします。⇒https://peatix.com/event/3014647/view

この記事の主な内容

1.はじめに

こんにちは。和から講師の佐々木です。ロマ数トレラン「微分トポロジー」に関連して、トポロジー分野で有名な定理を解説していきます。第1回はブラウワーの不動点定理をご紹介しました。

トポロジー有名定理その１～ブラウワーの不動点定理～

続く第２回はジョルダン・ブラウワーの分離定理です。

2.ジョルダンの閉曲線定理

複素関数の積分経路などで、自己交叉のないループ（閉曲線）のことを「単純閉曲線」と呼びますが、トポロジーではこのような、円周\(S^1\)の平面\(R^2\)への埋め込み（※1）の像をジョルダン曲線と呼んでいます。

ジョルダンと言えば、行列のジョルダン標準形やジョルダン細胞を思い浮かべる方が多いかもしれません。ジョルダン閉曲線のジョルダンさんも、同じ人。フランスの数学者カミーユ=ジョルダン（1838-1922）です。

なぜジョルダン曲線と呼ぶのか、それはこの定理からきたものと思われます。

ジョルダンの閉曲線定理
ジョルダン曲線によって、平面は内部（有界）と外部（非有界）の２つの連結領域に分けられる。

　
何とも当たり前な定理だと思いますよね。普通に考えて、単純閉曲線の内側と外側はそれぞれ連結だし、それ以外は線上の点しかなさそうです。しかし、閉曲線が多角形（折れ線）や多項式で表されている場合だけでなく、コッホ曲線（フラクタル図形）のようなどこもかしこも微分不可能な曲線についても本当に成り立つといえるでしょうか？　（ただし、曲線が\(S^1\)の「埋め込み」の像という条件から、平面内のある部分を稠密に埋め尽くすような曲線はジョルダン曲線とは言いません）

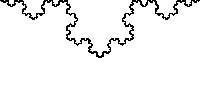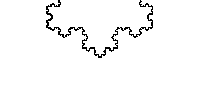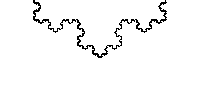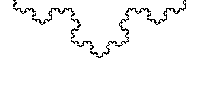
最初にこの主張が自明ではないことに気づいて定式化したのはボルツァーノ(1781-1848)といわれています。代数トポロジーが生まれる前の19世紀にこの事実を証明するのは大変でしたが、1887年、前述のジョルダンが実解析学の講義のなかで一般の曲線を折れ線で近似する方法を用いて証明しました。

しかし1905年、ジョルダンの証明には誤りがあるとのオズワルド＝ウェブレンの主張により、その後約100年もの間、最初の証明はウェブレンによるものとされていました。ところが、2007年トーマス・C・ヘイルズが“Jordan’s proof of the Jordan Curve theorem”のなかで、当初のジョルダンの証明には何の問題もなかったことを指摘。現在では、やはり最初に証明したのはジョルダンであるとされています。

3.ジョルダン・ブラウワーの分離定理

さて1911年、上のジョルダンの閉曲線定理を一般次元に拡張した定理を、(ルベーグ積分で有名な)アンリ=ルベーグと、(ブラウワーの不動点定理で有名な)L.E.J.ブラウワーがそれぞれ独立に証明しました。これをジョルダン・ブラウワーの分離定理と言います。

ジョルダン・ブラウワーの分離定理(\(n\geq 2\))
\(n-1\)次元球面\(S^{n-1}\)の\(R^n\)への埋め込みの像を\(X\)とするとき、\(X\)の補集合\(R^n\setminus X\)は、有界(\(X\)の内部)と非有界(\(X\)の外部)の2つの連結成分からなり、これらの共通の境界が\(X\)である。

　
\(n=2\)のときがジョルダンの閉曲線定理です。

\(X\)は、\(n=3\)のとき\(3\)次元空間内の球面\(S^2\)と同相な閉曲面、一般には\(n\)次元空間内の単連結な閉じた超曲面です(ポアンカレ・ペレルマンの定理により、単連結な閉多様体は\(S^{n-1}\)に同相なものしかありません)。

この定理は、現在ではホモロジー群のマイヤー・ビートリス完全系列を用いて証明するのが一般的ですが、ロマ数トレラン「微分トポロジー入門」では、写像の\({\rm mod}2\)巻き数に注目して、受講生の皆さんと一緒に証明していきます。(滑らかな埋め込みに限定して証明)

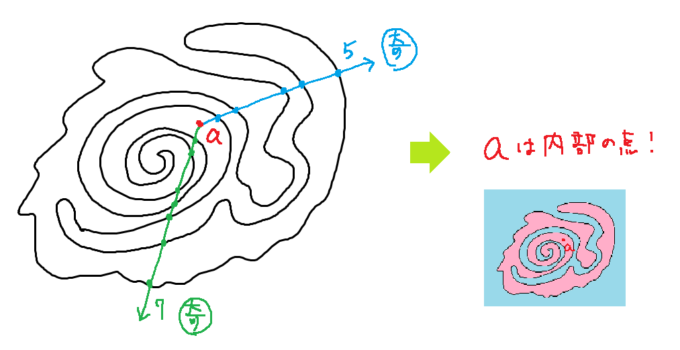
直感的に言って、超曲面Xの内部の点とは\(X\)によって一重に取り巻かれている点、外部の点とは\(X\)に取り巻かれていない点ですよね。それを判定するために、次のような「巻き数」を考えます。

包含写像\(f:X\rightarrow R^n\)と、\(R^n\setminus X\)の点\(a\)に対して、写像\(u∶X\rightarrow S^{n-1}\)
\[
u(x)=\frac{f(x)-a}{|f(x)-a|}
\]
が同じ方向を何回指し示すか（\(z\)を始点とする半直線と\(X\)との交点数に対応）を数え、それを2で割った余りを\({\rm mod}2\)巻き数\(W_2(f,a)\)と呼びます。これが\(0\)なら外部、\(1\)なら内部の点、と判定できます。（詳しくはトレランで）

4.シェーンフリース問題とアレクサンダーの角付き球面

ジョルダン・ブラウワーの分離定理により、\(R^n\)の単連結な閉超曲面は、必ず\(R^n\)を内部と外部の２つの領域に分けるとわかりましたが、これら2つの領域の形については何が言えるでしょうか。これについて考えたのが次のシェーンフリース問題です。

シェーンフリース問題(\(n\geq 2\))
\(n-1\)次元球面\(S^{n-1}\)の\(R^n\)への埋め込みの像を\(X\)とするとき、\(X\)の内部と外部はそれぞれ、標準的な単位球面\(S^{n-1}\)の内部と外部に同相（※2）だろうか？

　
\(n=2\)のときはシェーンフリース問題は正しい、つまり、ジョルダンの閉曲線の内部と外部は単位円の内部と外部に同相であることが証明されており、これをジョルダン・シェーンフリースの定理と言います。

では、\(n=3\)のとき、つまり\(3\)次元空間に埋め込まれた\(2\)次元球面\(X\)についてはどうでしょうか。　当然、\(X\)の内部と外部は単位球面の内部と外部に同相になりそうですが、実は反例が作られています。それが次のアレクサンダーの角付き球面です。

何個も何個も無限に角を出すお化けのようなこの立体の表面は2次元球面と同相です(角の先端がくっつくことは永遠にありません)。これを\(X\)とすると、\(X\)の内部は単連結ですが、外部は単連結ではなく(角の一本に絡まった輪っかを外すことは永遠にできない)、単位球面の外部の空間と同相になりえません。つまり、\(n=3\)のとき、シェーンフリース問題は成り立たないのです。

実は、この角付き球面は、「位相多様体」ではありますが、「滑らかな多様体(可微分多様体)」ではありません。シェーンフリース問題において、「同相」を「微分同相(※3)」や「PL同相(※4)」に強めると、このような反例は起こり得ず、\(n=3\)でもジョルダン・シェーンフリースの定理が成り立つことがアレクサンダーによって示されました。このことがトポロジーにおいてTOP圏, PL圏、DIFF圏とカテゴリーを分けるきっかけになったと言われています。

5.おわりに

どうでしたか。当たり前と思われる定理の証明が大変難しかったり、ときに反例が発見されてしまったり･･････、直感とはいかに当てならないものか、と驚いてしまいますね。

ところで、アレクサンダーの角付き球面のオブジェが、マルセイユのシャトーゴンベール大学の構内にあるようです。ぜひフランスに行って実物を見てみてたいと思っています。

次回はボルスク=ウラムの定理をご紹介します。
<文/佐々木和美>

TAGS :

記事一覧はこちら

マスログ